4. Использование методов математической статистики в судовождении

4. А

4. ББ

1. Статистические оценки числовых характеристик случайных величин

Несмотря на то, что все понятия теории вероятностей, включая и числовые характеристики случайных величин, являются абстрактными, отражают реальные закономерности, существующие в массовых явлениях. Это означает, что и числовые характеристики, и законы распределения случайных величин, и значение самой вероятности могут быть получены из наблюдений, проведением эксперимента.

Разработкой методов регистрации, описания и анализа результатов наблюдений массовых случайных явлений занимается математическая статистика.

Теоретически полученное значение вероятности можно подтвердить экспериментально, когда известна полная группа событий. Например, вероятность выпадения герба при бросании монеты равна 0,5. Это означает, что, если два раза бросить монету, один раз должен выпасть герб.

Сравнение экспериментально полученной вероятности с теоретическим значением показывает, что экспериментальное значение может отличаться от теоретического, но чем больше количество опытов, тем это отличие меньше.

В отличие от теоретического, экспериментальное значение вероятности называют частотой события Р*, и она определяется как отношение случаев, благоприятствующих этому событию k к общему числу опытов n.

.

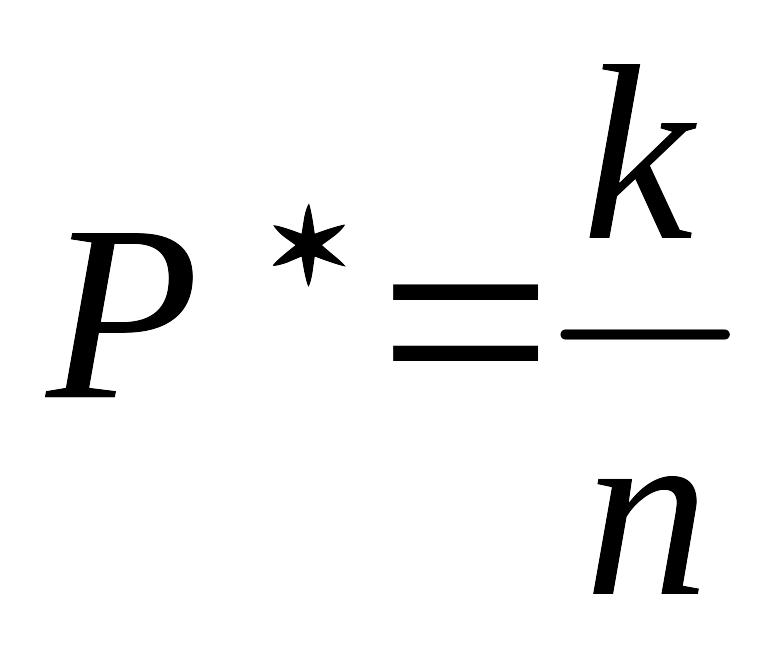Так, например, если сто раз бросить монету и 48 раз выпадет герб, частота его появления 0,48. По мере увеличения числа бросаний частота будет приближаться к 0,5.

Применительно к случайным величинам эксперимент подразумевает измерение. Если случайная величина (дистанция до ориентира) была измерена 5 раз и получены значения 38 кб, 35 кб, 36 кб, 37 кб, 36 кб, то частота значения 36 кб равна 0,4, а каждого из остальных − 0,2. В общем случае, если результаты измерений не повторяются, а произведено п измерений, то частота каждого измерения равна 1/п.

Таким образом, понятие вероятности в математической статистике заменяется понятием частоты.

Основными числовыми характеристиками элементов навигационной информации являются математическое ожидание и дисперсия. Они описываются формулами −.

В подавляющем большинстве случаев регистрация результата измерения является дискретным процессом. Дискретными будут и измеренные значения случайной величины. Для описания их характеристик используются формулы и .

Если в формуле вероятность заменить частотой, получим выражение для статистического аналога математического ожидания, который называется средним арифметическим

.

Как правило, число измерений ограничено и среднее значение случайной величины, полученное по формуле , от серии к серии измерений будет варьироваться. Поэтому говорят об оценке среднего значения, полученного по результатам измерений.

Оценка, несмотря на свой случайный характер, может достаточно точно характеризовать случайную величину, так как к ней предъявляется ряд требований.

Во-первых, оценка должна быть состоятельной. Это означает, что при увеличении числа измерений х₀ по вероятности должно сходится к математическому ожиданию случайной величины.

Во-вторых, оценка должна быть несмещенной. Это означает, что математическое ожидание оценок х₀, полученных по различным сериям, должно стремиться также к математическому ожиданию случайной величины.

В-третьих, оценка должна быть эффективной. Это означает, что из всех возможных, данная оценка должна обладать наименьшей дисперсией.

Выражение удовлетворяет всем перечисленным требованиям и служит оценкой математического ожидания случайной величины. Обычно оно обозначается как х_ср.

Если в формуле вероятность заменить частотой, а математическое ожидание его оценкой, получим выражение для статистической дисперсии:

.

Из перечисленных требований выражение удовлетворяет первому и третьему, т.е. оценка по этой формуле получится смещенной (несколько уменьшенной). Чтобы устранить смещение, статистическую дисперсию надо умножить на коэффициент п/(п-1). Тогда формула для оценки дисперсии будет выглядеть так:

.

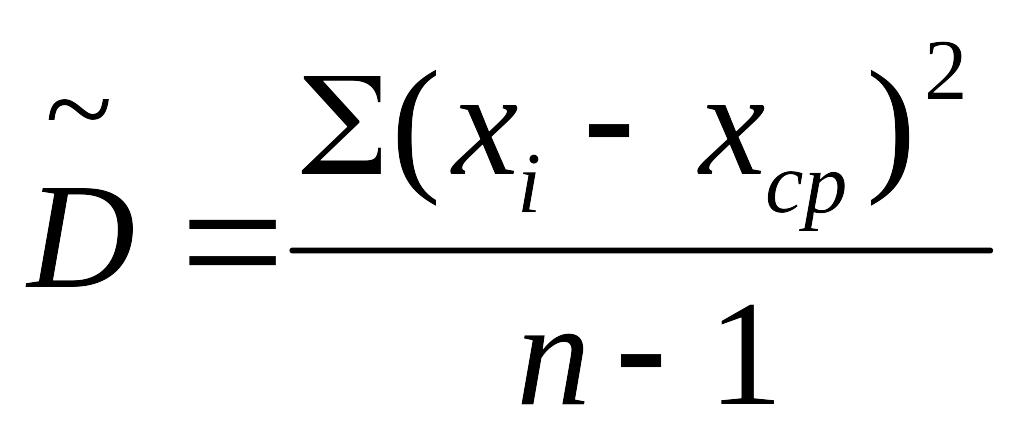Таким образом, формулы и используются для оценок математического ожидания и дисперсии случайной величины.

В соответствии с формулой оценкой среднего квадратического отклонения служит выражение

.

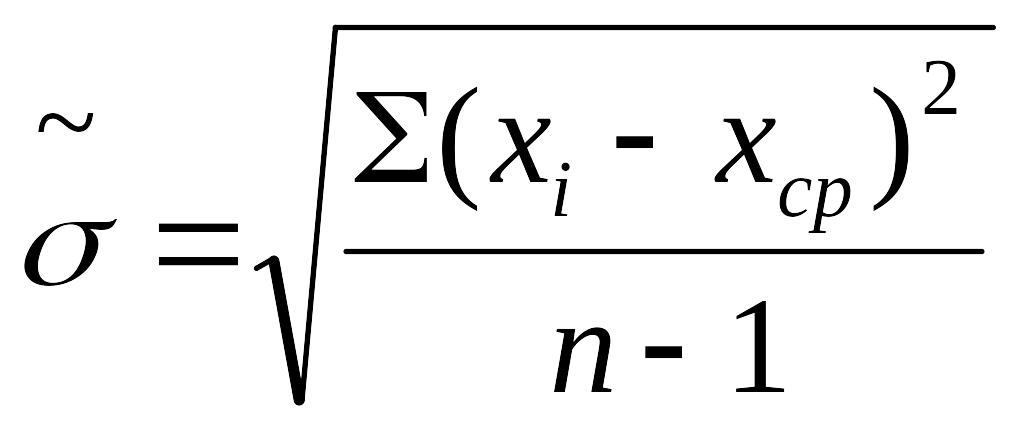При измерениях отклонение от среднего является следствием случайных погрешностей. Поэтому называют средней квадратической погрешностью, а сама формула называется формулой Бесселя по имени немецкого астронома 19 века. В литературе для судоводителей средняя квадратическая погрешность обычно обозначается буквой т.

Рассмотренные характеристики участвуют в описании системы случайных величин, случайных функций и процессов.

Аналогично дисперсии получаются оценки:

корреляционного момента

;

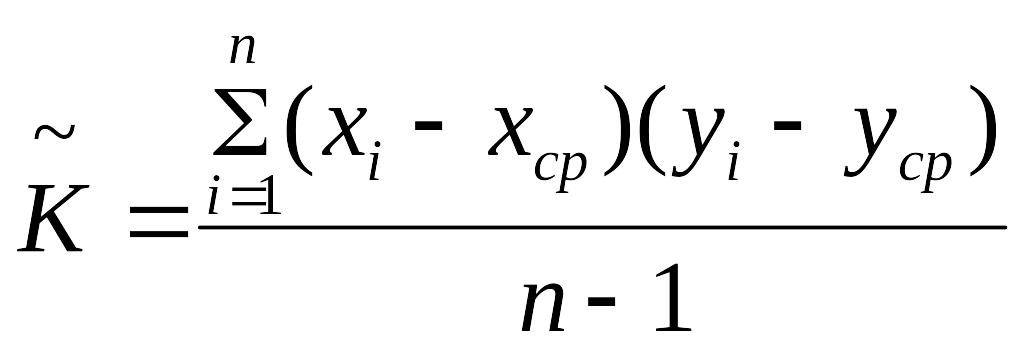коэффициента корреляции

;

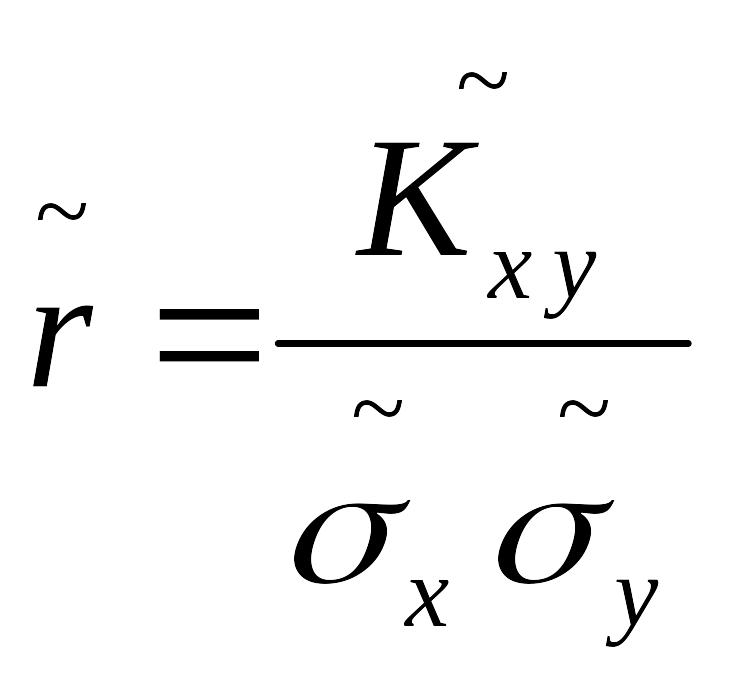корреляционной функции

;

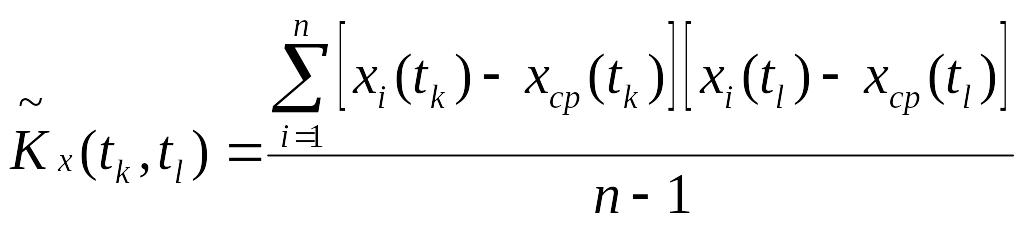автокорреляционной функции

,

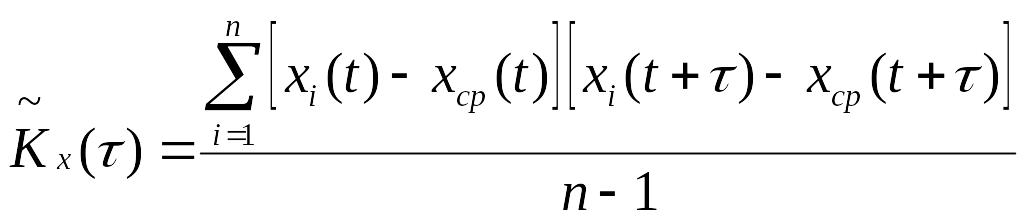где i − номер реализации; п − количество реализаций; k , l − номер сечения.