5. Случайные функции, случайные процессы

Случайной функцией называется функция, которая в результате опыта принимает то или иное, заранее неизвестное значение. Например, наклонение горизонта зависит от высоты глаза наблюдателя, но при его измерении в различных точках мирового океана из-за изменения коэффициента земной рефракции эта зависимость будет разной. Таким образом, наклонение горизонта является случайной функцией высоты глаза наблюдателя.

Если аргументом случайной функции является время, то ее называют случайным процессом. Например, курс судна на заданном прямом отрезке является случайным процессом из-за воздействий ветра, волнения, перекладки руля.

Рассмотрим основные понятия и характеристики случайных процессов. Допустим, судно несколько раз проходит один и тот же отрезок и фиксируется его курс в зависимости от времени. Совокупность значений курса в каждый момент времени, называется реализацией данного случайного процесса, а курсограмма является записью этой реализации.

По аналогии со случайной величиной под случайным процессом подразумевают все возможные его реализации.

На рис. 3.6 показаны несколько реализаций случайного процесса.

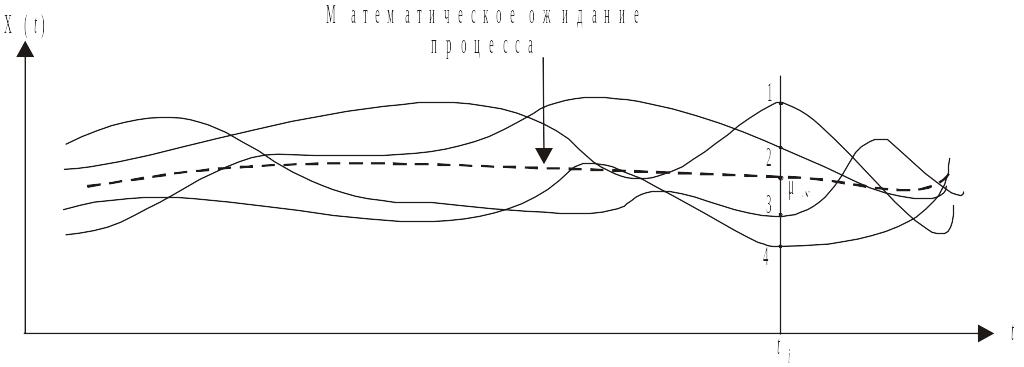
6. Реализации случайного процесса.

Сечение этого процесса по времени (t_i = const) является случайной величиной. Значения х_i на рис. 3.6 обозначены цифрами. Эта случайная величина имеет свое математическое ожидание μ_х и дисперсию D_x. Возьмем другие сечения по времени и также определим для них математические ожидания и дисперсии.

Совокупность математических ожиданий по всем сечениям образует математическое ожидание случайного процесса. Аналогично совокупность дисперсий по всем сечениям образует дисперсию случайного процесса.

Таким образом, математическое ожидание случайного процесса μ_х(t) − это неслучайная функция по времени, которая в каждый момент времени принимает значение, равное математическому ожиданию соответствующего сечения. Это некоторая кривая, вокруг которой группируются все реализации случайного процесса.

По аналогии со случайной величиной определяется центрированный случайный процесс и его дисперсия. Дисперсия случайного процесса D_x(t) − это неслучайная функция по времени, которая в каждый момент времени принимает значение, равное дисперсии соответствующего сечения. Извлекая квадратный корень из D_x(t) , получим среднее квадратическое отклонение случайного процесса.

7. Типы случайных процессов.

Рассмотренные характеристики являются очень важными, но они не полностью характеризуют процесс. Рассмотрим рис. 3.7. На нем изображены два случайных процесса, имеющие одинаковое математическое ожидание и дисперсию. Цифрами 1 и 2 показано два сечения через одинаковый интервал времени . Если в реализации первого процесса отклонение х(t) от математического ожидания за этот интервал времени изменилось незначительно, то в реализации второго процесса оно даже поменяло знак.

Э

то означает, что с увеличением времени между сечениями их зависимость в первом случае сохраняется довольно долго, а во втором − быстро затухает.

Таким образом, характер этих процессов различен, но это различие не отражает ни математическое ожидание, ни дисперсия. Поэтому вводится еще одна характеристика − корреляционная функция, которая отражает степень зависимости сечений процесса.

Корреляционная функция K_x (t₁,t₂). – это неслучайная функция, которая для каждой пары аргументов t₁ и t₂ равна корреляционному моменту соответствующих сечений.

.

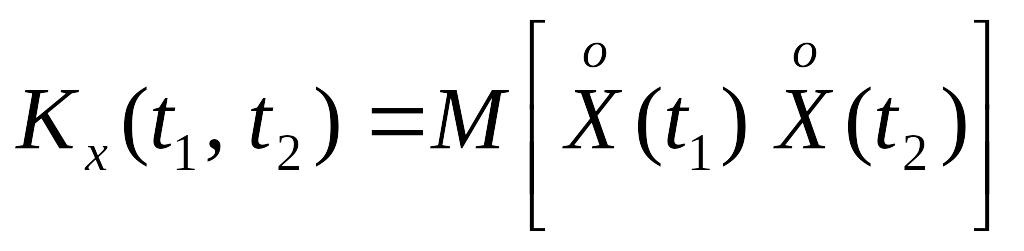Если интервал времени взять равный 0, корреляционная функция обращается в дисперсию.

Корреляционная функция, как следует из формулы , зависит от двух аргументов: начального момента t₁ и интервала времени до t₂. Если же корреляционная функция не зависит от начального момента, а только от интервала времени, такой процесс называют стационарным, а сама корреляционная функция называется автокорреляционной функцией K_x( ).

.

Обратимся снова к рис. 3.7 Если для Х₂ (t) любую одну реализацию продолжить по времени, то ее значения повторяют значения всех остальных реализаций. В результате по одной реализации можно получить все характеристики процесса: и математическое ожидание, и дисперсию, и корреляционную функцию. Можно сказать, что каждая реализация Х₂ (t) представляет другие. Если характеристики случайного процесса могут быть получены по одной реализации, то такой процесс называют эргодическим.

Для процесса Х₁ (t) каждая отдельная реализация имеет свое математическое ожидание и не отражает остальные реализации.