4. Системы случайных величин

Под системой понимают две или несколько случайных величин, рассматриваемых совместно. Например, значения крена, дифферента и рыскания в данный момент, погрешности в широте и долготе и т.п. Для двух случайных величин Х и Y система геометрически обычно представляется плоскостью, на которой можно перебрать все возможные сочетания х и y . Такие сочетания будут случайными, как и сами величины.

Рассмотрим три различных варианта таких сочетаний, которые показаны на рис. 3.5.

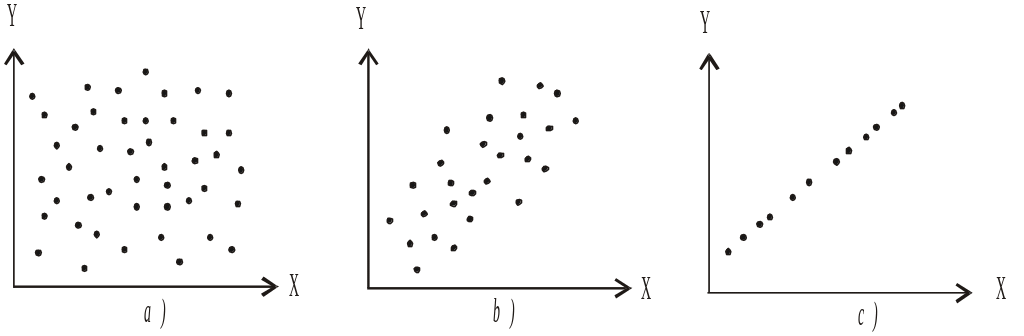
5. Системы случайных величин

На рис. 3.5 а) каждому значению Х может соответствовать любое значение Y.

На рис. 3.5 b) каждому значению Х соответствует определенный интервал, в котором может находиться Y. Причем, этот интервал при увеличении Х смещается вверх по оси Y.

Наконец, на рис. 3.5 с) каждому значению Х соответствует всего одно значение Y. В этом случае говорят о жесткой зависимости между Х и Y. Такую зависимость называют функциональной

Во втором случае зависимость просматривается, но она не такая однозначная, как функциональная. Такую зависимость называют стохастической.

В первом же случае нет никакой зависимости, т.е Х и Y независимы.

Таким образом, системы случайных величин различаются степенью зависимости или теснотой связи.

Достаточно полно система двух случайных величин может быть охарактеризована математическими ожиданиями Х и Y, их дисперсиями, а также математическим ожиданием произведения центрированных случайных величин:

.

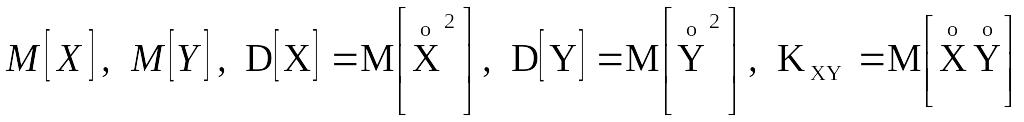где − центрированные относительно математических ожиданий случайные величины.

Первые две характеристики представляют средние значения случайных величин, и называются характеристиками положения, вторая пара (дисперсии) отражает разброс по осям Х и Y, последняя характеристика называется корреляционным моментом и является показателем тесноты связи или меры взаимозависимости этих величин.

Для дискретных случайных величин корреляционный момент выражается формулой , для непрерывных − .

;

.

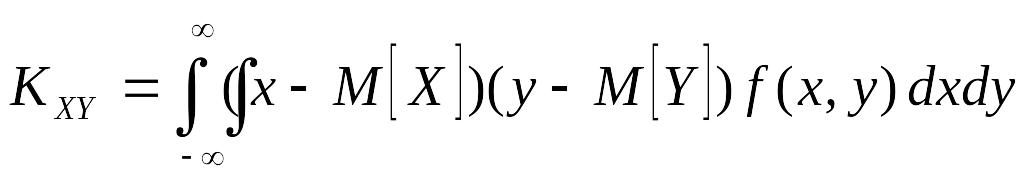Корреляционный момент имеет размерность произведения случайных величин. Чтобы перейти к безразмерной характеристике, его делят на произведение средних квадратических отклонений, в результате чего получают коэффициент корреляции

.

Коэффициент корреляции может быть в пределах от 0 до ±1. Чем ближе коэффициент корреляции к 1, тем теснее зависимость. Для функциональной зависимости r = 1, для независимых величин r = 0. Стохастическую зависимость называют также корреляционной.

Здесь следует заметить, что для независимых Х и Y корреляционный момент (и коэффициент корреляции) равен 0, но обратное утверждение верно только для нормально распределенных величин, т.е. у некоторых зависимых систем (распределенных не по нормальному закону), он может быть равен 0.

Коэффициент корреляции характеризует линейную зависимость, причем, со знаком «+» положительную корреляцию (при возрастании Х возрастает Y, рис. 3.5 b) ) и со знаком «-» − отрицательную корреляцию (обратная зависимость).

Если зависимость может быть представлена уравнением прямой, то r = 1 (рис. 3.5 с)).

Дисперсии случайных величин и корреляционный момент составляют так называемую корреляционную матрицу

.

Матрица может быть записана для любого количества случайных величин и, так как K_ху =K_ух , иногда ее представляют верхней от диагонали дисперсий частью.

Обычно достаточно знать только взаимозависимость случайных величин безотносительно к их разбросу. Для этого все элементы корреляционной матрицы делят на произведение соответствующих средних квадратических отклонений. Тогда вместо корреляционных моментов будут стоять коэффициенты корреляции, а по диагонали − единицы. Такая матрица называется нормированной корреляционной матрицей

.

Нормальный закон распределения для системы случайных величин

Плотность распределения системы величин f (x,у) определяется на основании теоремы умножения законов распределения и равна произведению плотности распределения одной величины на условную плотность распределения другой величины. Под условной понимают плотность распределения при условии, что другая величина приняла заданное значение.

Для произвольного количества случайных величин х₁, х₂ …. х_п плотность вероятности их совместного появления равна

.

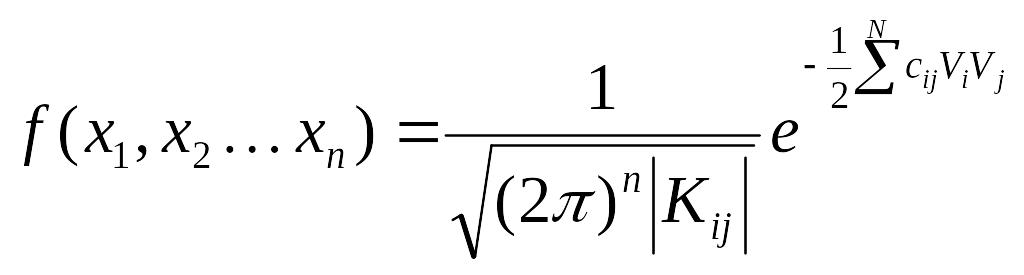где: − определитель корреляционной матрицы;

V = x_i − _x − отклонение случайной величины от математического ожидания;

c_ij − элементы матрицы, обратной к корреляционной;

n − количество случайных величин;

N = п² − общее число слагаемых.

В принятых ранее обозначениях плотность распределения системы двух любых случайных величин можно записать в виде

.

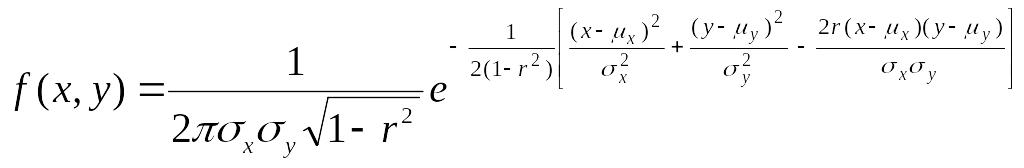Если величины независимы, коэффициент корреляции r равен 0, выражение (5.23) упрощается:

.

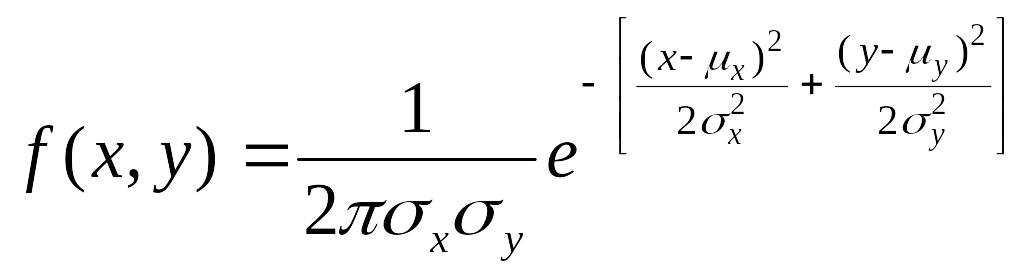Нормальный закон распределения системы в виде и используется при оценке точности обсервации соответственно по зависимым и независимым навигационным параметрам.