Розрахункова частина

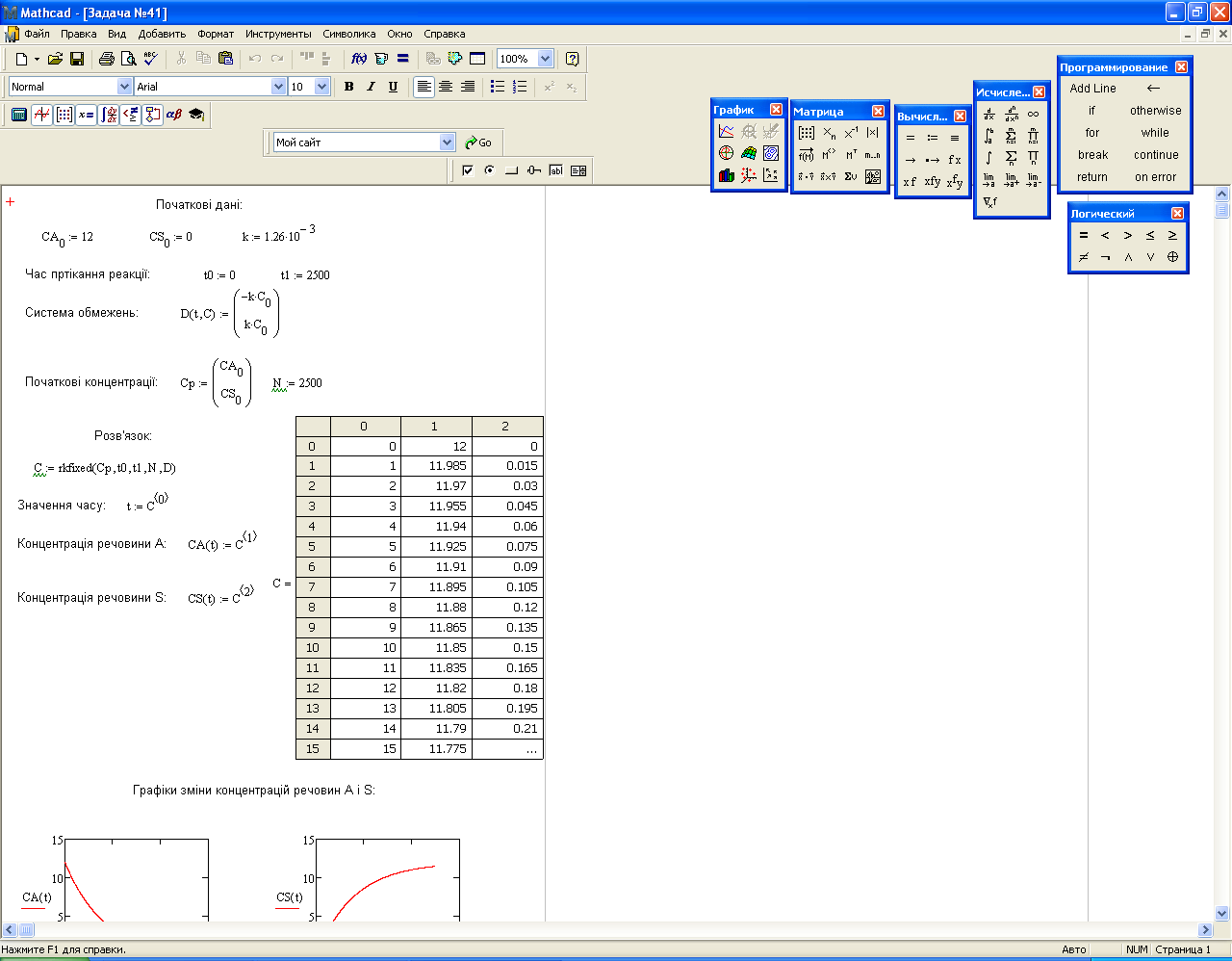
Мал. 2.1

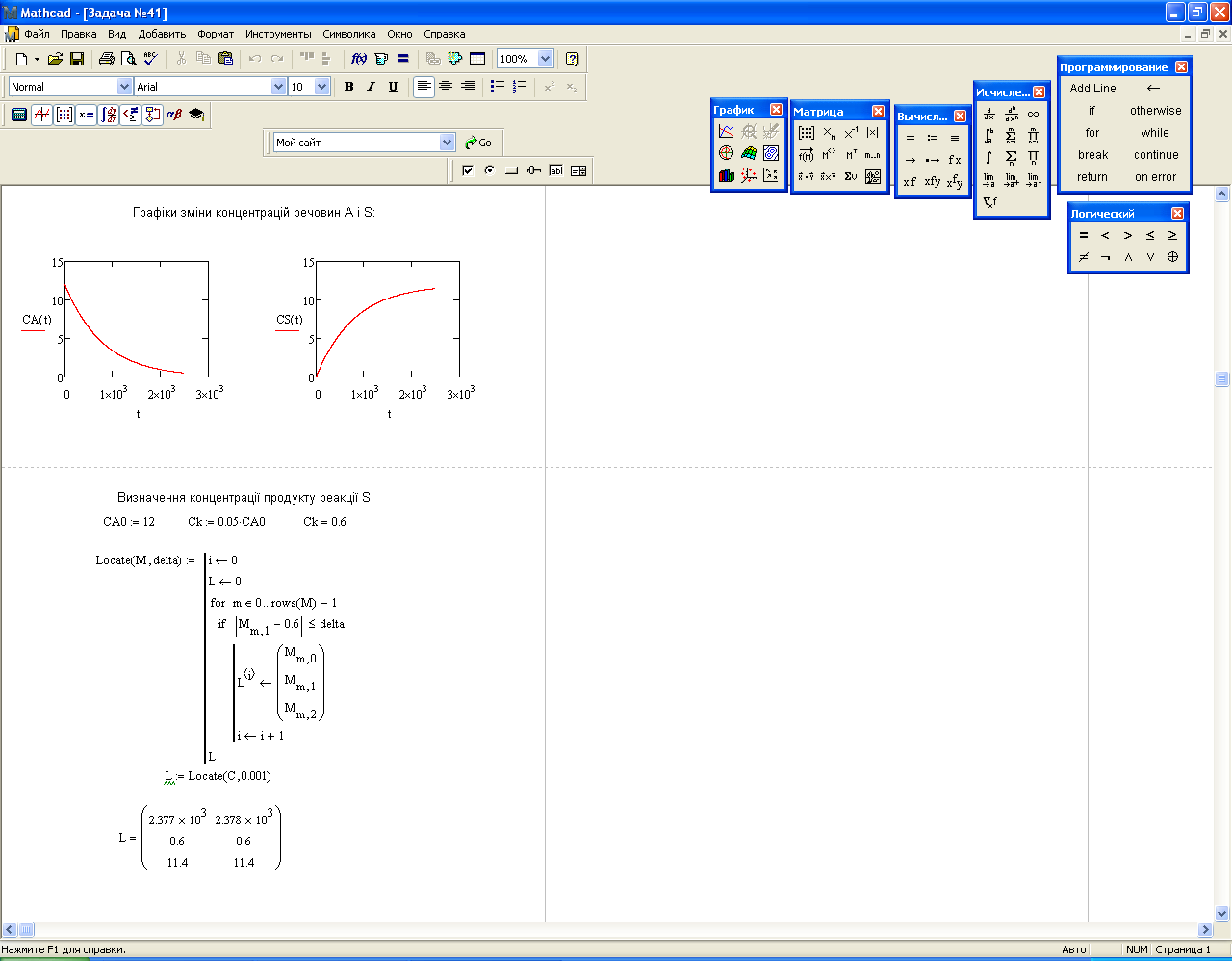
Мал. 2.2

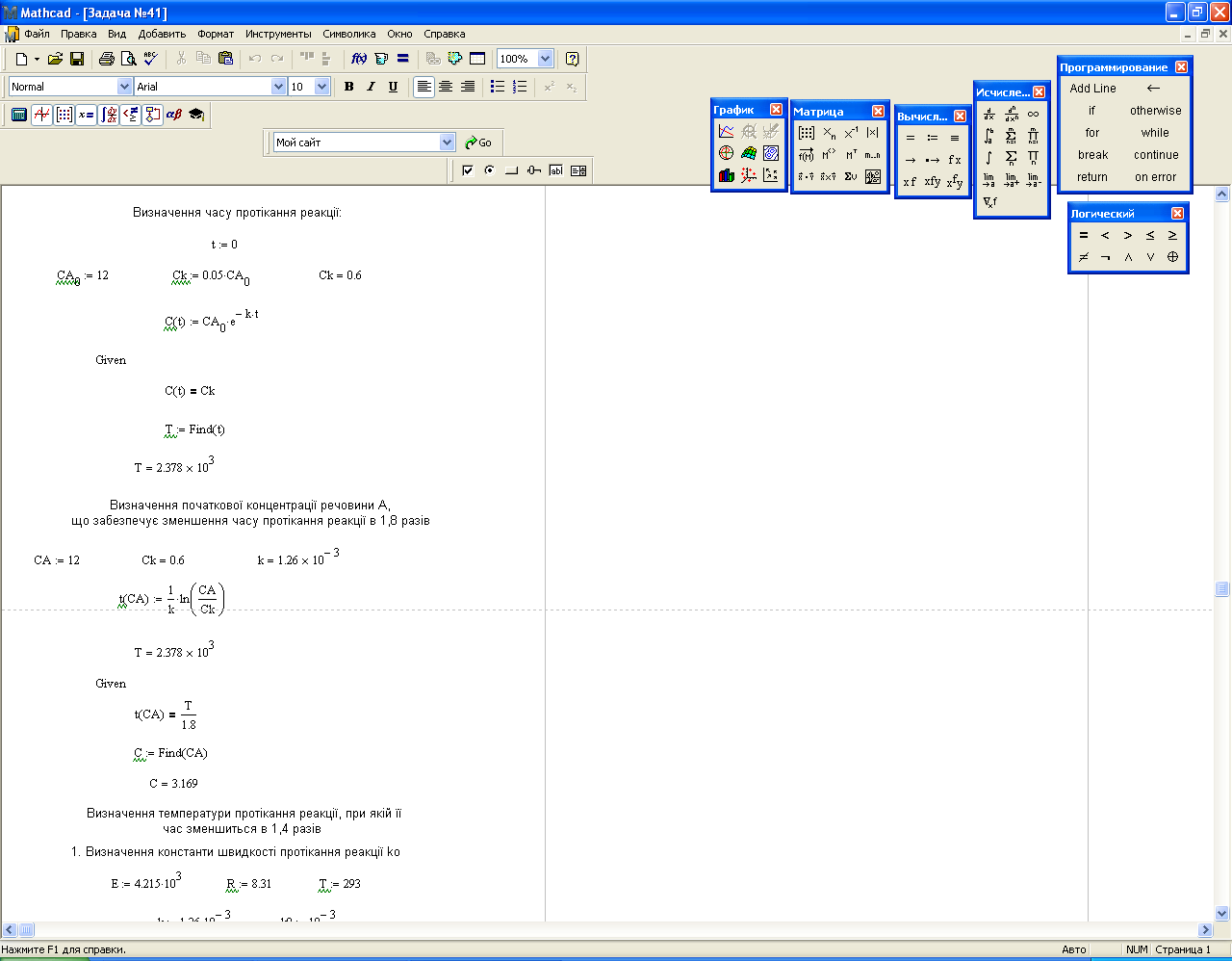
Мал. 2.3

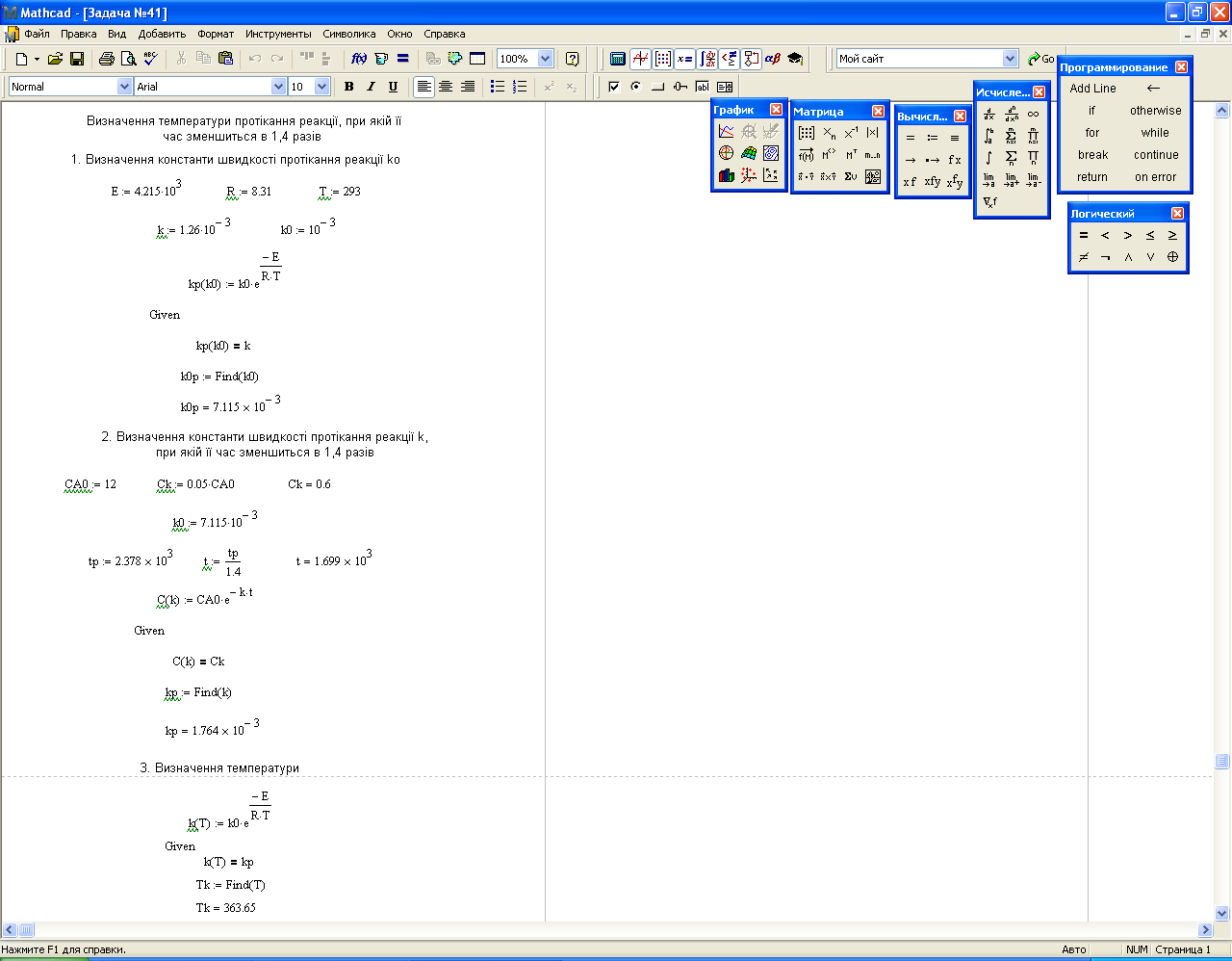
Мал. 2.4

Висновки

1. Концентрація реагенту А досягне 5% значення від початкового, тобто С_А=5% ^. С_А0 або С_А = 0,6 г/м³ на 2,378 ^. 10³ с.

2. Для того, щоб час реакції зменшився в 1,8 разів, за побудованою моделлю початкова концентрація речовини А має дорівнювати 3,169 г/м³.

3. Для того, щоб час реакції зменшився в 1,4 разів, за побудованою моделлю температура протікання реакції має становити 363,65 К.

4. Результуюча концентрація продукту реакції S за побудованою моделлю дорівнює 11,4 г/м³.

Задача № 65

Впродовж 10 днів працювали три аптечних кіоски.

Визначити, чи існує відмінність між обсягами реалізації препаратів у кіосках. Якщо так, то вибрати кіоск із найменшим обсягом реалізації препаратів.

Дані про роботу кіосків за десять днів представлені такою таблицею:

Обсяг реалізації препаратів, ум. од.	День
	1	2	3	4	5	6	7	8	9	10
Кіоск 1	125	175	140	110	170	225	170	180	210	215
Кіоск 2	190	220	90	140	250	330	190	240	250	210
Кіоск 3	160	180	120	160	200	230	250	180	200	280

Рівень значущості α=0,05

Теоретична частина

Для визначення відмінності між обсягами реалізації в аптеках доцільно вико­ристати однофакторний дисперсійний аналіз.

Дисперсійним аналізом називають сукупність методів оцінювання впливу різ­номанітних факторів на результативну ознаку досліджуваних об'єктів шляхом порів­няння вибіркових факторіальної і випадкової дисперсій.

Суть дисперсійного аналізу полягає в порівнянні показників розсіювання (ва­ріації) результативної ознаки щодо середніх значень під впливом організованих і не­організованих (випадкових) факторів.

Фактор - це причина мінливості ознаки, тобто дія, ефект, властивість, якість тощо.

Фактори впливу на ознаку поділяють на:

• організовані або контрольовані, величина яких під час дослідження контролюєть­ся;

• неорганізовані або неконтрольовані (випадкові), величина яких є випадковою і під час дослідження не контролюється.

Організовані фактори прийнято позначати А, В, С, ..., а результативні ознаки – X, У тощо.

Величину (рівень) кожного з факторів можна поділити на градації (підрівні), які прийнято позначати А₁,А₂, А₃, ... або В₁ і, В₂, В₃, ... тощо.

Градації факторів визначають за їх впливом на результативну ознаку.

Вибіркова сукупність експериментальних даних, що відповідним чином пред­ставлена для вивчення ефективності впливу організованих факторів на результативну ознаку, називається статистичним або дисперсійним комплексом.

Дисперсійний комплекс на практиці представляють у вигляді таблиці, струк­тура якої визначається кількістю градацій, на які поділяються організовані фактори.

У залежності від кількості організованих факторів дисперсійні комплекси поді­ляють на однофакторні, двофакторні і багатофакторні.

За характером розподілу результатів експериментальних спостережень (варі­ант) за градаціями дисперсійні комплекси поділяють на рівномірні, пропорційні і не­рівномірні.

У найпростішому випадку дисперсійного аналізу розглядається вплив на ре­зультативну ознаку X одного (основного) фактора А.

Нехай цей фактор має m кількісних чи якісних градацій, відповідно до яких увесь дисперсійний комплекс поділяють на m груп. Дисперсійний комплекс зручно представити у вигляді таблиці:

Градації фактора А	А1	А2	…	Аm
Значення результативної ознаки Х	x11, x12, …, x1n1	x12, x22, …, x2n2	…	xm1, xm2, …, xmnm
Об’єм вибірки за градаціями	n1	n2	…	nm

де

x_ik – k-а варіанта, що відноситься до і-ої групи, k=1, 2, …, n_i,

n_i – об’єм і-ої групи, причому кожна група характеризується своїм груповим середнім арифметичним значенням , де і = 1, 2, …, m,

m – кількість груп варіант відповідно до числа градацій організованих факторів,

- сума об’ємів вибірки за градаціями, що дорівнює загальному об’єму дисперсійного комплексу.

Однофакторний дисперсійний аналіз здійснюють у такій послідовності:

1. Визначають загальне для всього дисперсійного комплексу середнє арифметичне значення результативної ознаки:

.

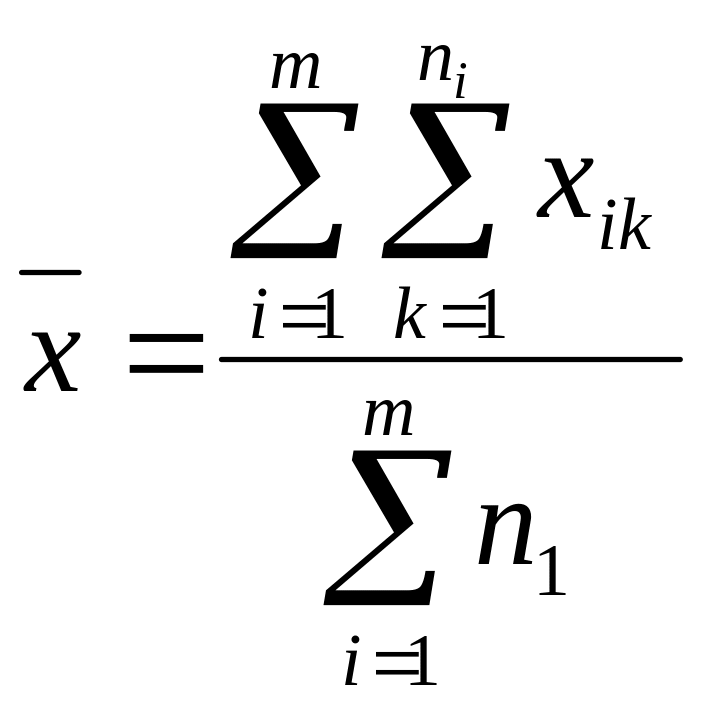2. Визначають групові середні ,тобто середні арифметичні значення результативної ознаки для кожної градації фактора А:

.

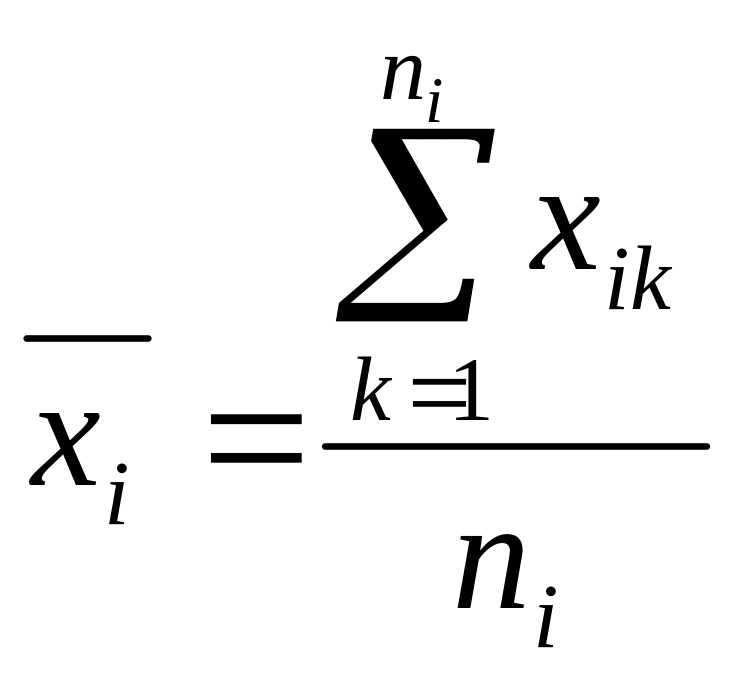3. Обчислюють факторіальне розсіювання С_х як суму квадратів відхилень групових середніх 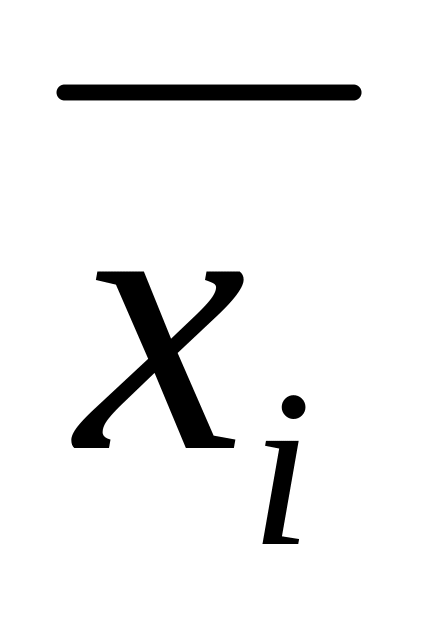від загального середнього арифметичного значення, помножених на об’єм вибірки за градаціями n_i:

.

4. Обчислюють випадкове розсіювання C_z:

.

5. Обчислюють загальне розсіювання C_y:

С_y = С_x + С_z

6. Обчислюють відношення

,

за допомогою якого визначають вплив на результативну ознаку фактора А.

7. Обчислюють відношення

,

за допомогою якого визначають вплив на результативну ознаку випадкових (неорганізованих) факторів.

8. Обчислюють загальну дисперсію результативної ознаки

,

де v_y = n – 1 – кількість ступенів вільності.

9. Обчислюють факторіальну дисперсію

,

де v_x = m – 1 – кількість ступенів вільності.

10. Обчислюють випадкову дисперсію

,

де v_z = n – m – кількість ступенів вільності.

11. Обчислюють відношення факторіальної дисперсії до випадкової дисперсії

,

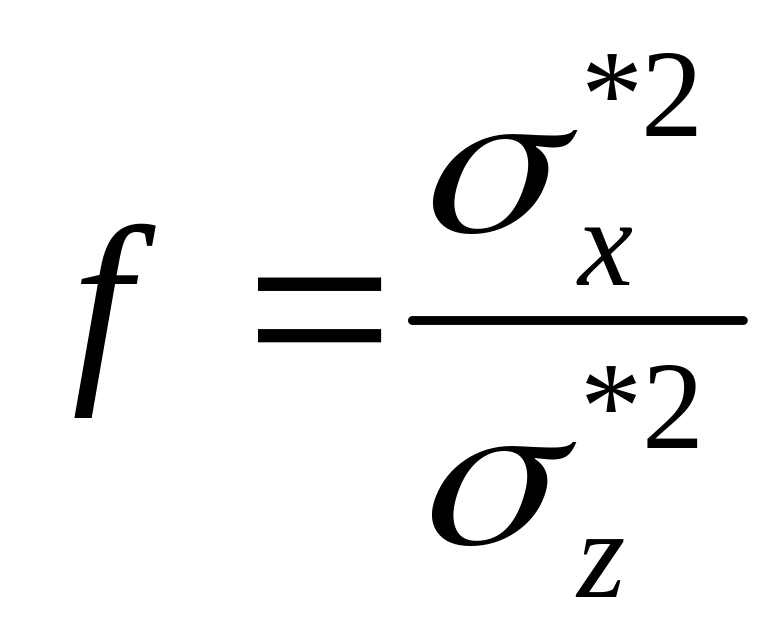за допомогою якого оцінюють вірогідність впливу фактора А на результативну ознаку X.

Випадкова величина F підпорядковується розподілу Фішера з числом ступенів вільності за умови, що результативна ознака Х нормально розподілена з однаковою дисперсією в кожній групі дисперсійного комплексу.

Якщо має місце нерівність f > f*, то формулюють висновок про наявність достовірного (P = 1 – α 0,95) впливу фактора, що вивчається, на результативну ознаку. Критичне значення

знаходять за таблицею розподілу Фішера-Снедекора для заданої надійної ймовірності Р = 1 – α 0,95 чи рівня значущості .

Вплив фактора А вважають недостовірним чи недоведеним, якщо f > 1 і має місце нерівність , де

і

визначені за таблицею розподілу Фішера-Снедекора.

Використовуючи однофакторний дисперсійний аналіз перевіряють гіпотези:

Н₀: середні значення результативної ознаки на всіх рівнях факторної ознаки однакові, вплив фактора на результативну ознаку недостовірний;

Н₁: мають місце зміщення центрів розподілу досліджуваної ознаки, обумовлені дією фактора, або вплив фактора на результативну ознаку достовірний;

α – рівень значущості.

Перевіряють нульову гіпотезу за допомогою критерію Фішера на рівні значу­щості α, значення якого f, а також критичне значення f* знаходять, використовуючи пакет аналізу програми MS Excel.

Якщо f > 1 і буде мати місце нерівність f < f*, то нульова гіпотеза не відхиляється. Отже, вплив фактора на результативну ознаку не­достовірний.

Якщо f < 1 , то, використовуючи розподіл Фішера, слід знайти за допомогою функції РРАСПОБР() Майстра функцій програми MS Excel значення і , вра­ховуючи, що

і

,

де

n – об’єм вибірки(дисперсійного комплексу),

m – кількість градацій фактора.

Якщо буде мати місце нерівність , то факторіальна і випадкова дисперсії відрізняються незначно, вплив фактора на результативну ознаку недостовірний.