30

Міністерство охорони здоров’я України

Івано-Франківський національний медичний університет

Кафедра медичної інформатики,

медичної і біологічної фізики

Завідувач кафедри

професор Мойсеєнко М. І.

Комп'ютерні технології у фармації

Курсова робота

Номер залікової книжки 01-08

Варіант 01

Задачі 2, 41, 65

Виконав

студент 41 групи IV курсу

фармацевтичного факультету

Бойчук Ігор

Д

Івано-Франківськ – 2011

Зміст

1. Задача № 2 ………………………………………………………….3

2. Задача № 41 ………………………………………………………..14

3. Задача № 65 ………………………………………………………..22

4. Список використаної літератури………………………………….30

Задача №2

З’ясували значущість різниці між способами А, Б, В і Г обробки сировини з точки зору виходу продукту.

Дані представлені в таблиці:

Спосіб обробки сировини	Величина виходу продукту, ум. од.
А	82	84	82	83	81	82	84	-
Б	92	91	90	92	93	93	91	-
В	90	92	93	91	92	91	92	94
Г	104	98	99	100	105	-	-	-

Мета – визначити спосіб обробки сировини, при якому вихід продукту мінімальний.

Рівень значущості α=0,05.

Теоретична частина

Для того, щоб вирішити задачу, необхідно з’ясувати, чи має місце відтворюваність експерименту, тобто перевірити статистичну гіпотезу про однорідність дисперсій.

Для того щоб з’ясувати, чи має фактор статистично значущий вплив на результативну ознаку досліджуваних об’єктів, необхідно здійснити дисперсійний аналіз.

Перевірка відтворюваності експерименту

Під час аналізу однорідності дисперсій перевіряють статистичні гіпотези:

H₀: дисперсії дослідних груп (вибірок) належать до однієї генеральної сукупності, тобто однорідні;

H₁: дисперсії дослідних груп (вибірок) неоднорідні;

α – рівень значущості.

Для оцінки однорідності дисперсій у випадку різної кількості повторних дослідів у кожній вибірці застосовується критерій Бартлета:

,

де

, ,

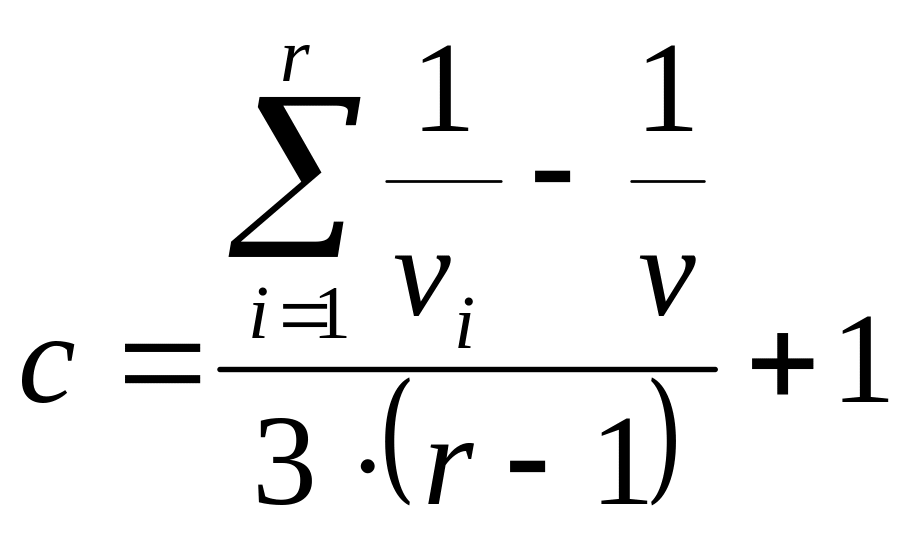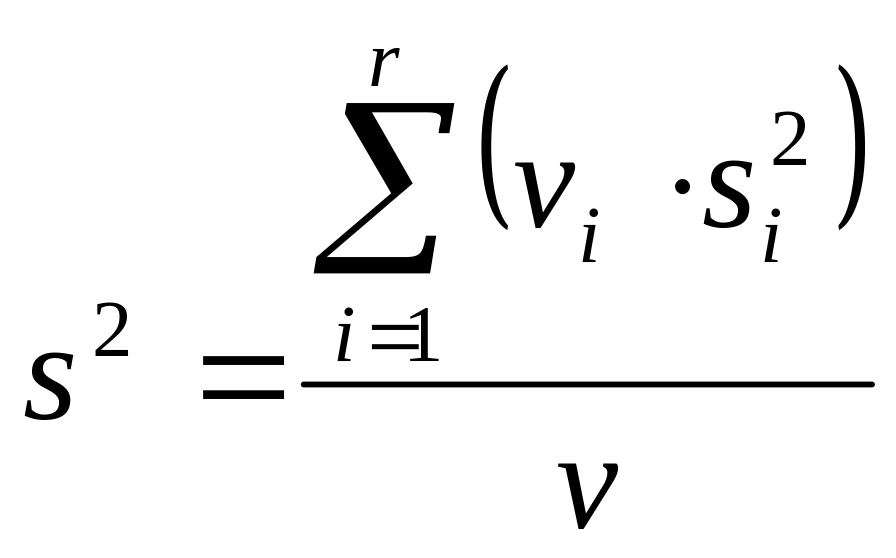k_i – об’єм і-ї дослідної групи,

v_i = k_i - 1 – кількість ступенів вільності в кожній дослідній групі,

- загальна кількість ступенів вільності,

r – градацій фактора або дослідних груп,

- оцінка дисперсії в кожній і-й дослідній групі,

s² – зважена оцінка дисперсії.

Вважають, що на рівні значущості α або з ймовірністю р=1-α дисперсії належать до однієї генеральної сукупності, тобто гіпотеза про однорідність приймається, якщо виконується нерівність .

Критичне значення критерію Бартлета

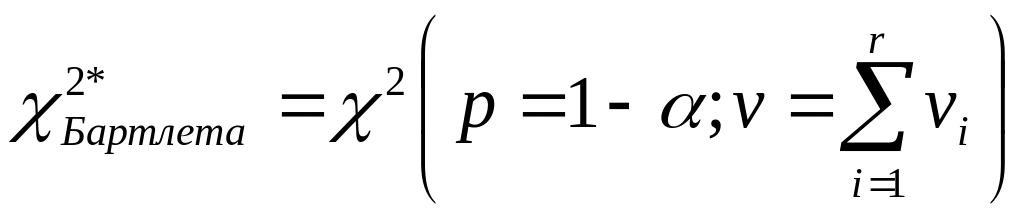
визначають за таблицею - розподілу.

Дисперсійний аналіз

Під час аналізу однофакторного експерименту перевіряють статистичні гіпоте­зи:

H₀: рівні фактора за впливом на досліджувану результативну ознаку об'єктів не від­різняються;

Н₁: фактор має статистично значущий вплив на досліджувану ознаку;

α — рівень значущості.

З цією метою використовують критерій Фішера, числове значення якого у ви­падку однофакторної задачі з нерівномірним числом випробувань знаходять, викорис­товуючи такий алгоритм:

1. Визначають загальну суму квадратів за формулою:

,

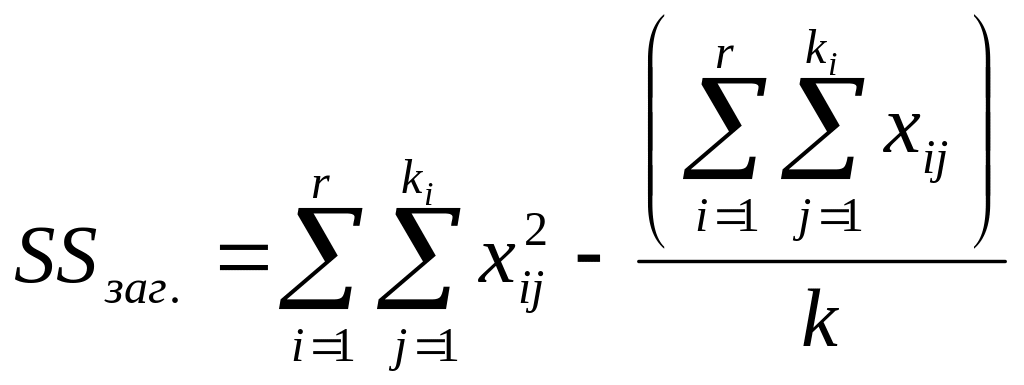де

x_ij – j-те значення в і-й дослідній групі,

r – кількість градацій фактора або дослідних груп,

k_i – кількість спостережень в і-й дослідній групі,

- об’єм дисперсійного комплексу або загальна кількість спостережень

2. Визначають факторіальну (міжгрупову) суму квадратів за формулою:

.

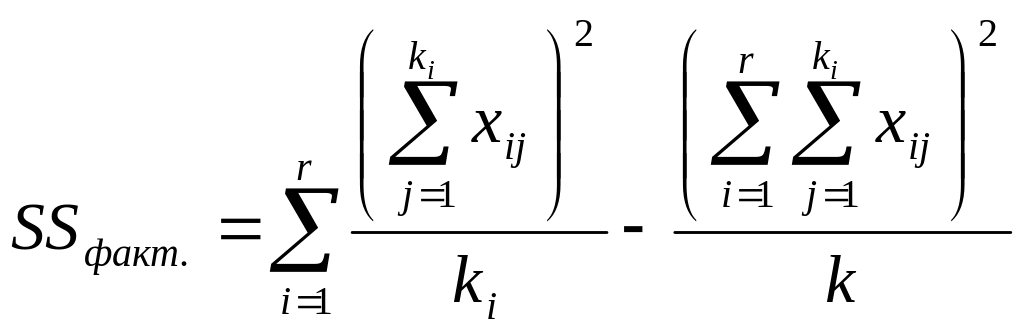3. Визначають залишкову (внутрішньогрупову) суму квадратів за формулою:

.

4. Обчислюють залишкову (внутрішньогрупову) і факторіальну (міжгрупову) дисперсії за формулами:

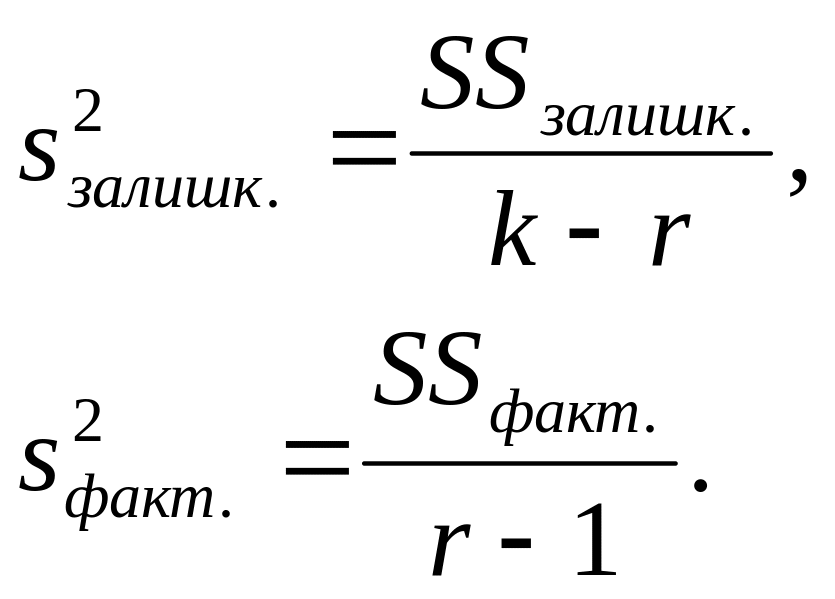
5. Обчислюють значення критерію Фішера за формулою:

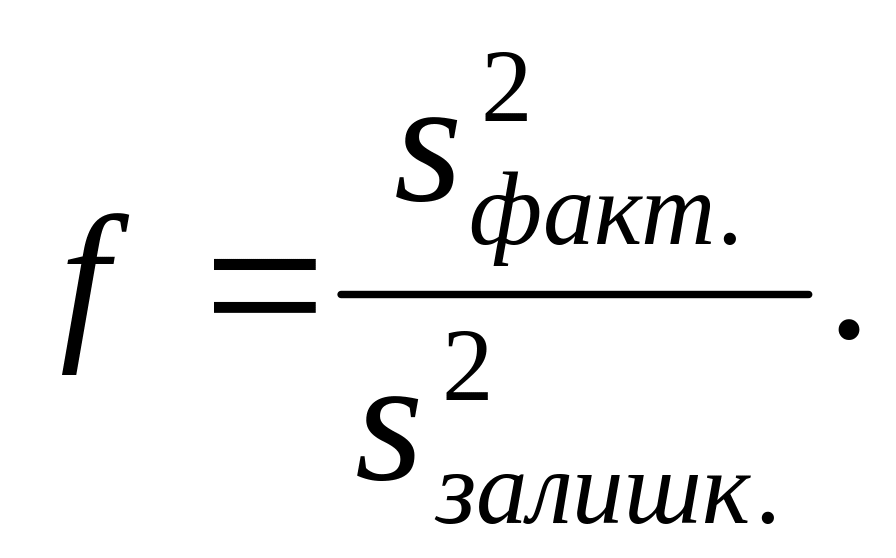
Якщо буде мати місце нерівність f < f *, то нульова гіпотеза не відхиляється.

Критичне значення критерію Фішера визначають за таблицею розподілу Фішера.

Якщо матиме місце нерівність F < F_{критическое} , то нульова гіпотеза не відхиляється.