Лекция №8

ЛОГИЧЕСКИЕ ОСНОВЫ ПОСТРОЕНИЯ ПК

Для автоматизации обработки информации необходимо, прежде всего, выбрать способ ее представления в машине и технические средства реализации арифметических и логических операций.

Большинство используемых в настоящее время вычислительных машин являются цифровыми, а не аналоговыми.

В аналоговых машинах для представления чисел служат непрерывно изменяющиеся физические величины, такие как давление, перемещение или напряжение. Простейшим примером аналоговой машины является логарифмическая линейка. В электронных аналоговых вычислительных машинах расчеты выполняются с помощью электронных схем, рабочие характеристики которых моделируют процесс вычислений. Например, для моделирования операции сложения двух чисел можно использовать схему, выходное напряжение которой представляет сумму двух входных напряжений. Электронные аналоговые вычислительные машины используются для моделирования в реальном времени физических систем, описываемых сложными дифференциальными уравнениями.

Отличительной чертой цифровых вычислительных машин является то, что они осуществляют хранение и обработку величин, представляющих собой цифры. Большинство физических явлений, используемых в современных вычислительных устройствах, характеризуются двумя устойчивыми состояниями, каждое из которых соответствует одной из двух цифр: "1" высокий потенциал в точке схемы, "0" низкий (потенциальный код); "1" наличие импульса тока, "0" отсутствие импульса (импульсный код); "1" транзистор открыт, "0" транзистор заперт; "1" участок поверхности намагничен, "0" размагничен. Следовательно, цифровые машины производят обработку двоичных цифр, или битов, принимающих значения 0 или 1.

В схемах цифровых устройств переменные и соответствующие им сигналы изменяются не непрерывно, а лишь в дискретные моменты времени. Временной интервал между двумя соседними моментами дискретного времени называется тактом.

Для анализа и синтеза схем в ЭВМ при алгоритмизации и программировании задач широко используется математический аппарат алгебры логики.

Математическая логика современная форма логики, опирающаяся на формальные математические методы.

Алгебра логики — это раздел математической логики, значения всех элементов (функций и аргументов) которой определены в двухэлементном множестве: 0 и 1. Алгебра логики оперирует с логическими высказываниями.

Основные объекты логики - высказывания, то есть предложения, которые могут быть либо истинными, либо ложными. При этом считается, что высказывание удовлетворяет закону исключенного третьего, т.е. каждое высказывание или истинно, или ложно и не может быть одновременно и истинным, и ложным.

Существуют два подхода установления истинности высказываний: эмпирический (опытный) и логический.

При эмпирическом подходе истинность высказываний устанавливается на основе наблюдений, экспериментов, документов и других фактов.

При логическом подходе истинность высказываний доказывается на основе истинности других высказываний, то есть чисто формально, на основе рассуждений без обращения к фактам.

Множество всех логических функций, на котором определены три логические операции И, ИЛИ, НЕ называется булевой алгеброй (по имени основоположника математической логики английского математика Джорджа Буля).

Логические элементы и логические функции. Элементы математической логики

Логическая функция – это функция логических переменных, которая может принимать только два значения: 0 или 1. В свою очередь, сама логическая переменная (аргумент логической функции) тоже может принимать только два значения: 0 или 1.

Логический элемент – это устройство, реализующее ту или иную логическую функцию. Y = f (X1, X2, X3, ..., Xn) – логическая функция. Она может быть задана таблицей, которая называется таблицей истинности.

X1, X2, X3, …, Xn	Y = f(X1, X2, X3, …, Xn)
Набор значений аргументов (0 или 1) X1, X2, X3, …, Xn	Значение функции Y (0 или 1)

При любом фиксированном упорядочении наборов значений переменных логическая функция п переменных полностью определена вектором-столбцом своих значений, т.е. вектором длины 2ⁿ. Поэтому число строк в таблице – это число возможных наборов значений аргументов и оно равно 2ⁿ, а число различных функций n переменных равно 2²ⁿ.

Существуют такие наборы логических функций, с помощью которых можно выразить любые другие логические функции. Они называются функционально полными или базисами.

Наиболее известный базис это набор функций И, ИЛИ, НЕ. Функция штрих Шеффера является базисной, также как и функция стрелка Пирса. Поэтому, с помощью логических элементов ИЛИ-НЕ или И-НЕ можно собрать любую логическую схему. На таких элементах собран микропроцессор компьютера и другие логические устройства. Логические схемы состоят из логических элементов, осуществляющих логические операции.

Таким образом, логика – наука, изучающая методы установления истинности или ложности одних высказываний на основе истинности или ложности других высказываний (утверждений). Логика изучает методы доказательств и опровержений. Логика составляет основу всякого управления, в том числе технологическими процессами.

Логические функции одной переменной

Таблица истинности функции одной переменной Y = f(X) содержит всего 2 строки, а число функций одной переменной равно 4.

1. Функция константа 0, Y=0. Техническая реализация этой функции соединение вывода Y с общей шиной с нулевым потенциалом.

Таблица истинности функции константа 0 имеет вид:

X	Y= f(x)
0	0
1	0

2. Функция Y = f(X) = X функция повторения. Техническая реализация этой функции соединение между собой выводов X и Y. Таблица истинности функции повторения имеет вид:

X	Y= f(x)
0	0
1	1

3 . Функция Y = f(X) = NOT(X) = X отрицание НЕ или инверсия (NOT(X) – это НЕ X). Техническая реализация этой функции инвертор на любом транзисторе или логическом элементе, или транзисторный ключ.

Таблица истинности функции отрицания имеет вид:

X	Y= f(x)
0	1
1	0

Логический элемент НЕ обозначается на схемах следующим образом: (пишется X c чертой сверху):

	1 (НЕ)
Х		Y = Х

или так:

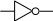Х Y

4. Функция константа 1, Y = 1. Техническая реализация этой функции соединение вывода Y с источником питания.

Таблица истинности функции константа 1 имеет вид:

X	Y = f(x)
0	1
1	1

Важнейшей функцией одной переменной является отрицание НЕ, остальные функции являются тривиальными.