25) Математические структурные схемы приборов контроля.

А)

Б)

В)

г)

Д)

На рисунке изображены математические структурные схемы прибора непосредственной оценки (рис а) и прибора со вторичным электрическим комплектом (рис б ). Схема изображенная на ( рис а ) характерна для приборов местных постов: пружинных манометров, вольтметров, амперметров, частотомеров, а показанная на ( рис б) – для приборов блочных и центральных щитов: расходомеров, приборов контроля давления, перепадов давления, уровнемеров.

26) Погрешности измерения и контроля

При анализе измерительных систем и приборов, установленных на МЩУ или ЦЩУАЭС наибольший интерес представляет оценка общей, т.е. статической и динамической погрешности.

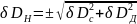
Или для относительных погрешностей

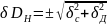
Где

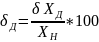
Погрешность 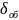можно определить как функцию скорости изменения контролируемой величины Сх

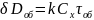
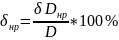
Для оценки верхнего предела времени обработки принимаем время обработки сигнала 60с. Контроль за правильностью действий 60-360с. Время от поступления сигнала до принятия решения 120-360с. Цветовое представление на дисплее информации: нормальное сост.- зелёный

Несрабатывание аппаратуры - красный

27)Информационное обеспечение контроля технологических процессов аэу.Количество информации от кип о состоянии аэс.

Оценим количественно неопределенность идентификации состояния АЭУ производимую человеком оператором с ПУТП на основе ИП. Рассмотрим прибор со шкалой 0,1…10

И допустим что отсутствуют все погрешности измерения . Тогда для различных уровней

амплитуды сигнала вероятность одного результата равна p=1\n

Мерой неопределенности в теории информации служит энтропия.

H=log(1\p)=-logp

В термодинамике говорят не об абсолютной величине, а только о приращении энтропии

delS=St1-St2 и H(x)изм=H(x)исх-H(x)рас

где St1 и H(x)исх- исходные энтропии

Если ничего не известно о значении параметров, то прибору верить не следует

P=1\n, n-наибольшая неопределенность

Энтропия измерений:

Hн=logn, J(x)= H(x)н- H(x)изм ,

Если p=1 H(x)изм=0

J(x)= H(x)н=logCn-информация

Если ничего не известно о значении

Наибольшая энтропия прибора

H(x)н=H(x)Dн

J(D,x)= H(x)Dн- H(x)D1

D2,D3,Dm

J(D2,x), J(D3,x),….., J(Dm,x)  H(x)Dн

J(D,x)= H(x)Dн- H(x)D

Первый предельный случай:

Использование для контроля «не того прибора» X и D независимы и J(D,x)=0

Второй случай:

Прибор D дает об объекте X исчерпывающую информацию H(x)D=0 и J(D,x)= H(x)Dн

Если исключить грубые ошибки, но не идеализировать каналы передачи информации , то принятая информация всегда будет меньше максимальной J(D,x)< H(x)Dн

Зависимость между принимаемым D(t) и передаваемым X(t) сигналами эмпиически

D(t)= KX(t- τj)+Rj(t)

K-коэф передачи канала информации

28) Информационный парадокс помех при контроле аэс

Представим к-й контролируемый приборами выход АЭУ, как случайную величину Dk(t)=M(Dk)+R’k, где M(Dk) – среднее значение, R’k – центрированная случайная величина. В свою очередь R’k есть сумма R’k1 – шумовой составляющей контролируемого процесса и R’k2 – шумовой составляющей к – го прибора контроля. В таком представлении M(Dk) есть контролируемый сигнал, R’k – случайная помеха. Анализируемая информация представляет собой выходные данные о технологическом процессе и приборе или следствии процессов, протекающих в объекте и приборе контроля под действием некоторых случайных входных воздействий.