Лекция 7. Евклидовы и метрические пространства. Неравенство Коши-Буняковского. Существование ортонормированного базиса

В теории квадратичных форм важную роль играют евклидовы пространства и самосопряжённый оператор. Перейдем к описанию этих понятий.

1. Евклидовы и метрические пространства

Пусть линейное пространство над множеством действительных чисел

Определение 1. Пространство называется евклидовым пространством, если в нем для любой пары векторов и определено число называемое скалярным произведением и , удовлетворяющее следующим свойствам:

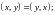1. П.О. 2. С. 3. Л.

(здесь произвольные векторы, произвольные числа).

Например, обычное скалярное произведение в геометрическом пространстве трехмерных векторов удовлетворяют свойствам 1-3, поэтому - евклидово пространство. Очевидно, что пространство ( мерных векторов-столбцов) также является евклидовым пространством со скалярным произведением

также является евклидовым пространством. Обычно евклидовы пространства обозначают буквой и мы будем пользоваться этим обозначением.

Если линейное пространство над множеством комплексных чисел и если в нем введено скалярное произведение удовлетворяющее аксиоме 1 и аксиомам

то пространство называется унитарным пространством (здесь черта вверху означает комплексное сопряжение: ). Мы будем рассматривать в основном евклидовы пространства. Однако все приводимые ниже понятия и утверждения почти дословно переносятся и на унитарные пространства.

Определение 2. Два вектора называются ортогональными, если

Имеет место следующее утверждение: любая система попарно ортогональных векторов в линейно независима. Действительно, пусть . Умножая это равенство скалярно на будем иметь

Таким образом, равенство выполняется тогда и только тогда, когда все числа одновременно равны нулю. Это означает, что векторы линейно независимы.

Определение 3. Базис пространства называется ортонормированным, если

Например, базис в пространстве является ортонормированным.

Введем теперь в рассмотрение понятие метрического пространства.

Определение 4. Линейное пространство называется метрическим пространством, если в нем для любых векторов и определено число называемое расстоянием между и (или метрикой в ), обладающее следующими свойствами:

4. П.О. 5. С. 6. Т.

( произвольные векторы из пространства ).

Любое евклидово пространство является одновременно и метрическим пространством с метрикой (проверьте выполнение свойств 4-6). Заметим, что число называется длиной (или нормой) вектора Так что в евклидовом пространстве

В любом евклидовом пространстве имеет место неравенство Коши-Буняковского:

Отсюда следует, что имеет смысл называемое косинусом угла между векторами и

Теорема 1. В любом евклидовом пространстве размерности существует ортонормированный базис . Координаты вектора в этом базисе имеют вид

Доказательство первой части этой теоремы проводить не будем. Перейдем ко второй части. Имеем . Умножая скалярно это равенство на будем иметь

Теорема доказана.

Введем следующее важное понятие.

Определение 5. Оператор действующий в унитарном (в частности, в евклидовом) пространстве называется сопряженным к оператору если для всех

имеет место равенство Обозначение:

Теорема 2. В любом ортонормированном базисе унитарного пространства матрица оператора является сопряженной по отношению к матрице оператора т.е. если матрица оператора то матрицей оператора будет матрица

И, наконец, заметим, что квадратная матрица называется симметрической, т.е. Нетрудно показать, что все собственные значения симметрической матрицы действительны; при этом и отвечающие им собственные векторы также можно выбрать действительными.