
- •Описание установки
- •Порядок выполнения работы
- •Контрольные вопросы.
- •3. Осветитель.
- •Условия интерференции.
- •2. Интерференция на тонкой плёнке.
- •3. Кольца Ньютона.
- •Описание установки
- •Порядок выполнения работы
- •Контрольные вопросы
- •Описание установки
- •Порядок выполнения работы
- •Контрольные вопросы.
- •Рекомендуемая литература
Порядок выполнения работы
Из формулы (4) следует, что радиус кривизны линзы
Для определения этого радиуса необходимо измерить радиусы (диаметры) колец Ньютона для определённой длины волны. Для этого:
1.
Установите зелёный светофильтр с длиной
волны 545 нм. Переключите увеличение
объектива микроскопа на
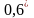 и передвигая линзу с пластинкой,
отъюстировать микроскоп до появления
в окуляре микроскопа картины
интерференционных колец Ньютона.
и передвигая линзу с пластинкой,
отъюстировать микроскоп до появления
в окуляре микроскопа картины
интерференционных колец Ньютона.
2. Постепенно меняя увеличение микроскопа в сторону увеличения отъюстировать микроскоп до заполнения кольцами всего поля окуляра (рис. 6). Следует проверить, что крест нитей окуляра проходит через середину центрального темного пятна.

Рисунок 6.
3. С
помощью линейки на экране подсчитать
число делений шкалы для пары колец,
начиная от центра до
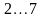 тёмного
кольца. Кольца выбирают, достаточно
далеко отстоящие друг от друга (например:
m
= 6, k
= 2 или m
= 5, k
= 1).
тёмного
кольца. Кольца выбирают, достаточно
далеко отстоящие друг от друга (например:
m
= 6, k
= 2 или m
= 5, k
= 1).
4. Для определения фактического радиуса колец Ньютона воспользоваться переводной таблицей 1.
Таблица 1.
Кратность увеличения |
1 деление шкалы 0,1 мм соответствует |
0,6* |
0,17 |
1 |
0,1 |
2 |
0,05 |
4 |
0,025 |
7 |
0,014 |
5. Заменить зелёный светофильтр на жёлтый с длиной волны 578 нм и произвести замеры согласно п.3.
6. Аналогичные замеры сделать для красного светофильтра с длиной волны 630 нм.
7. Данные измерений занести в таблицу 2.
8. Рассчитывают R линзы по формуле (4) для заданных длин волн и находят затем среднее значение R.
9. Затем
рассчитывают абсолютную погрешность
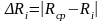 и вычисляют среднюю ошибку
и вычисляют среднюю ошибку
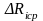 .
Окончательный результат записывают в
виде
.
Окончательный результат записывают в
виде
 .
.
Таблица 2.
Светофильтр |
Номер кольца |
Число делений шкалы |
Радиус кольца r, м |
Длина волны
|
|
|
|
|
Зелёный |
|
|
|
545 |
|
|
|
|
Жёлтый |
|
|
|
578 |
|
|
|
|
Красный |
|
|
|
630 |
|
|
|
|
Контрольные вопросы
1. Определение интерференции света, физическая картина интерференции.
2. Условия наблюдения интерференции света.
3. Какие волны являются когерентными?
4. Что называется оптическим ходом (оптической разностью хода) лучей?
5. Условия max и min при интерференции.
6. Интерференция света на тонких плёнках.
7. Условия max и min для колец Ньютона в отражённом и проходящем свете.
8. Вывод формулы радиусов m-го светлого и темного колец Ньютона в отражённом и проходящем свете.
Работа Б-4. Изучение явления дифракции света
Цель работы
Определить длину световой волны с помощью дифракционной решетки.
Приборы и принадлежности:
Гониометр.
Дифракционная решетка.
Краткая теория
Дифракцией света называется явление отклонения световых волн от прямолинейного распространения, когда световая волна, огибая препятствие, заходит в область геометрической тени.
Для наблюдения дифракции необходимо, чтобы длина волны света была соизмерима с размерами препятствия.
Явление дифракции света объясняется с волновой точки зрения и находится в тесной связи с явлением интерференции. Выяснить суть явления дифракции позволяет принцип Гюйгенса-Френеля. Согласно этому принципу:
К аждую
точку фронта волны следует рассматривать
как источник вторичных волн; эти вторичные
волны когерентны между собой и поэтому,
распространяясь в пространстве,
интерферируют между собой.
аждую
точку фронта волны следует рассматривать
как источник вторичных волн; эти вторичные
волны когерентны между собой и поэтому,
распространяясь в пространстве,
интерферируют между собой.
Таким образом, между явлениями интерференции и дифракции нет существенного физического различия. Оба явления заключаются в перераспределении энергии световых волн в результате их суперпозиции (наложения). Перераспределение интенсивности, возникающее в результате суперпозиции волн, исходящих из отдельных когерентных источников, принято называть дифракцией волн.
Для расчета дифракционной картины Френелем был предложен оригинальный метод, называемый методом зон Френеля. Основанием этого метода является интерференция вторичных волн, исходящих от каждой точки фронта волны. Суть метода зон Френеля заключается в том, что фронт волны мысленно разбивается на зоны так, чтобы разность хода граничных лучей от двух соседних зон составляла половину длины волны для данной точки наблюдения. Таким образом волны, исходящие от двух соседних зон приходят в выбранную точку наблюдения в противофазе и гасят друг друга.
Рассмотрим явление дифракции в параллельных лучах.
Дифракция от одной щели.
Пусть на узкую
щель шириной
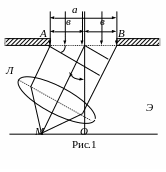
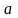 падает плоский фронт монохроматической
световой волны перпендикулярно плоскости
щели (рис.1).Все точки плоского фронта
АВ, вырезаемого щелью, являются
когерентными источниками вторичных
световых волн, которые за щелью
распространяются во всех направлениях
и при наложении интерферируют.
Дифракционная картина, то есть результат
интерференции вторичных волн, наблюдают
на экране Э, помещенном в фокальной
плоскости линзы Л.
падает плоский фронт монохроматической
световой волны перпендикулярно плоскости
щели (рис.1).Все точки плоского фронта
АВ, вырезаемого щелью, являются
когерентными источниками вторичных
световых волн, которые за щелью
распространяются во всех направлениях
и при наложении интерферируют.
Дифракционная картина, то есть результат
интерференции вторичных волн, наблюдают
на экране Э, помещенном в фокальной
плоскости линзы Л.
 Лучи,
идущие перпендикулярно от плоскости
щели имеют разность хода равную нулю
(
Лучи,
идущие перпендикулярно от плоскости
щели имеют разность хода равную нулю
(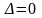 ).
На экране они собираются в фокусе линзы
в точке О и дадут в этой точке
центральный максимум.
).
На экране они собираются в фокусе линзы
в точке О и дадут в этой точке
центральный максимум.
Лучи, идущие под некоторым углом к первоначальному направлению, также соберутся в фокальной плоскости линзы, но уже в другой точке М на экране.
Выведем условие интерференции для этой группы лучей. Для этого разобьем волновой фронт АВ на зоны Френеля в виде узких полосок одинаковой ширины в, параллельных краям щели. Разность хода между двумя крайними лучами по условию равна . Следовательно, если в направлении уложится четное число зон, то в точке М будет наблюдаться минимум интенсивности света (темная полоса), если нечетное число зон – максимум интенсивности (светлая полоса).
В щели укладывается число зон
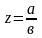 .
.
Из чертежа (рис.1)
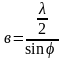
и число зон
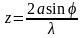 (1)
(1)
При четном числе зон, то есть при
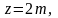 где
где
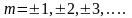 (2)
(2)
имеем минимум интенсивности. Приравнивая выражения (1) и (2) получаем условие минимума:
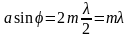 (3)
(3)
Целое число
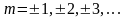 определяет порядок минимума. Первый
минимум имеет место при
определяет порядок минимума. Первый
минимум имеет место при
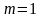 ,
то есть в том направлении, для которого
в щели укладывается четыре зоны, и т.д.
,
то есть в том направлении, для которого
в щели укладывается четыре зоны, и т.д.
Максимум интенсивности наблюдается при нечетном числе зон, то есть при
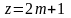 (4)
(4)
где .
Из выражений (1) и (4) получим условие максимума:
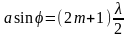 (5)
(5)
где
.-
порядок дифракционного максимума.
Первый максимум получим при
,
то есть когда в щели укладывается три
зоны; затем – при
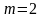 (пять зон) и т.д.
(пять зон) и т.д.
На экране
дифракционная картина имеет следующий
вид. В центре экрана имеет место
центральный максимум (точка О), в
которой интерферируют лучи, идущие под
углом
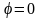 .
Для этих лучей разность хода равна нулю,
и они усиливают друг друга. По обе стороны
от центрального максимума чередуются
темные и светлые полосы соответствующего
цвета падающей длины волны
.
.
Для этих лучей разность хода равна нулю,
и они усиливают друг друга. По обе стороны
от центрального максимума чередуются
темные и светлые полосы соответствующего
цвета падающей длины волны
.
Если на щель
падает белый свет, то центральный
максимум представляет яркую белую
полоску, так как в точке О условие
максимума выполняется для всех длин
волн. Боковые максимумы спектральные,
обращенные фиолетовой полосой к
центральному. Это следует из того, что
по условию максимума (5)
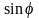 ~
,
то есть для меньшей длины волны угол
меньше для наблюдения максимума любого
порядка.
~
,
то есть для меньшей длины волны угол
меньше для наблюдения максимума любого
порядка.
Дифракционная решетка.
Одномерная
дифракционная решетка представляет
собой систему параллельных щелей
одинаковой ширины
,
лежащих в одной плоскости и разделенных
непрозрачными промежутками равной
ширины
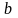 (рис.2).Величина
(рис.2).Величина
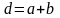 называется постоянной, или периодом
дифракционной решетки.
называется постоянной, или периодом
дифракционной решетки.
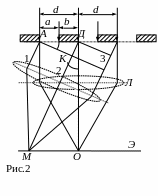 Если
на дифракционную решетку падает плоский
фронт монохроматической волны
перпендикулярно ее плоскости, то после
прохождения решетки, согласно принципу
Гюйгенса – Френеля, вторичные волны от
щелей решетки распространяются по всем
возможным направлениям и при наложении
интерферируют. Помещая на пути
распространения волн, идущих за решеткой,
собирающую линзу Л, на экране Э,
находящемся в фокальной плоскости
линзы, наблюдается дифракционная
картина: чередование светлых и темных
полос.
Если
на дифракционную решетку падает плоский
фронт монохроматической волны
перпендикулярно ее плоскости, то после
прохождения решетки, согласно принципу
Гюйгенса – Френеля, вторичные волны от
щелей решетки распространяются по всем
возможным направлениям и при наложении
интерферируют. Помещая на пути
распространения волн, идущих за решеткой,
собирающую линзу Л, на экране Э,
находящемся в фокальной плоскости
линзы, наблюдается дифракционная
картина: чередование светлых и темных
полос.
В случае дифракционной решетки условия максимума и минимума иные, чем при дифракции на одной щели, так как при прохождении света через систему щелей имеет место дополнительная интерференция волн.
Очевидно, что направление , в котором одна щель дает дифракционный минимум, будет направлением ослабления света и для всей системы щелей. Эти главные минимумы интенсивности света наблюдаются в направлениях, определяемых условием (3):
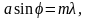
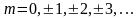
Если в направлении одна щель дает усиление интенсивности света (максимум), то вся система щелей в этом направлении может дать либо усиление, либо ослабление интенсивности света. В этом случае необходимо рассматривать условия интерференции соответственных лучей.
Соответственными лучами называются параллельные лучи, идущие под углом к первоначальному направлению от соответствующих точек щелей, находящихся на расстоянии друг о друга (лучи 1, 2, 3 и т.д. на рис.2).
Результат
интерференции любой пары соответственных
лучей определяется их разностью хода.
Из чертежа (рис.2) для лучей 2 и 3 разностью
хода является отрезок |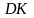 |,
равный:
|,
равный:
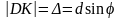 (6)
(6)
Если в
разности хода укладывается целое число
длин волн
(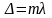 ),
то эти соответственные лучи усиливают
друг друга. Таким образом, это условие
главных дифракционных минимумов
определяется соотношением:
),
то эти соответственные лучи усиливают
друг друга. Таким образом, это условие
главных дифракционных минимумов
определяется соотношением:
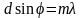 ,
(7)
,
(7)
Если в
разности хода соответственных лучей
укладывается нечетное число длин
полуволн
(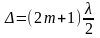 ),
то эти лучи гасят друг друга, то есть в
этом направлении возникают дополнительные
минимумы. Их условием является соотношение:
),
то эти лучи гасят друг друга, то есть в
этом направлении возникают дополнительные
минимумы. Их условием является соотношение:
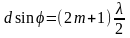 ,
(8)
,
(8)
Целое число называется порядком спектра дифракционного минимума или максимума.
Из условия
(7) при
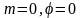 получаем положение центрального
максимума, имеющего нулевой порядок.
При
получаем положение центрального
максимума, имеющего нулевой порядок.
При
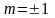 условие (7) определяет угол
,
в направлении которого наблюдаются
максимумы первого порядка, расположенные
вправо и влево от центрального максимума,
и т.д. Таким образом, в фокальной плоскости
линзы Л на экране Э наблюдается
следующая дифракционная картина:
центральная наиболее яркая и узкая
полоса и ряд постепенно убывающих по
яркости полос, симметрично расположенных
относительно центральной.
условие (7) определяет угол
,
в направлении которого наблюдаются
максимумы первого порядка, расположенные
вправо и влево от центрального максимума,
и т.д. Таким образом, в фокальной плоскости
линзы Л на экране Э наблюдается
следующая дифракционная картина:
центральная наиболее яркая и узкая
полоса и ряд постепенно убывающих по
яркости полос, симметрично расположенных
относительно центральной.
П ри
освещении дифракционной решетки белым
светом, как и в случае одной щели, на
экране наблюдаются дифракционные
спектры. Центральный максимум нулевого
порядка представляет яркую белую полосу,
так как из формулы (7) видно, что
соответствует максимуму при
для всех длин волн
.
Поскольку
ри
освещении дифракционной решетки белым
светом, как и в случае одной щели, на
экране наблюдаются дифракционные
спектры. Центральный максимум нулевого
порядка представляет яркую белую полосу,
так как из формулы (7) видно, что
соответствует максимуму при
для всех длин волн
.
Поскольку
 ~
,
то все остальные максимумы расположены
в спектральной полосе влево и вправо
от центрального и обращены фиолетовой
частью (наименьшая длина волны) к центру
(рис.3).
~
,
то все остальные максимумы расположены
в спектральной полосе влево и вправо
от центрального и обращены фиолетовой
частью (наименьшая длина волны) к центру
(рис.3).
Зная период дифракционной решетки и измеряя экспериментально угол и порядок спектра , из формулы (7) можно вычислить длину волны :
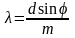 (9)
(9)
Таким
образом, задача определения длины волны
с помощью дифракционной решетки сводится
к измерению углов
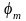 ,
в направлении которых наблюдаются
максимумы m -го порядка
для выбранной длины волны.
,
в направлении которых наблюдаются
максимумы m -го порядка
для выбранной длины волны.

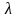 ,
нм
,
нм ,
м
,
м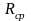 ,
м
,
м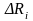 ,
м
,
м