Расстояние от точки до плоскости.

Пусть задана точка М₀(х₀;у₀;z₀) и плоскость Q своим уравнением Ах+Ву+Сz+D=0. Расстояние d от точки до пл-ти находится по формуле:

(Вывод формулы тако же как вывод формулы от точки до прямой)

Замечание:

Если пл-ть задана уравнением , то расстояние от точки М₀ до плоскости может быть найдено по формуле

Угол между прямыми в пространстве.

Пусть в пространстве заданы две прямые. Их параметрические уравнения:

l₁: l₂:

Угол между прямыми  и угол между направляющими векторами  этих прямых связаны соотношением:  = ₁ или  = 180⁰ - ₁. Угол между направляющими векторами находится из скалярного произведения. Таким образом: .

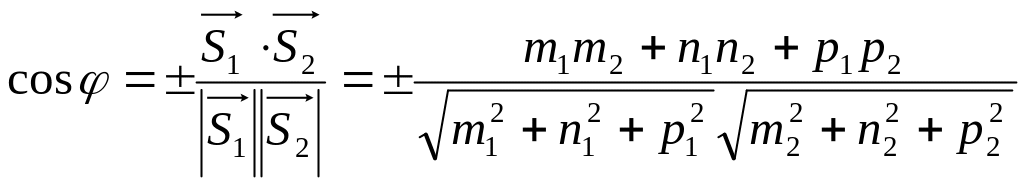Условия параллельности и перпендикулярности

прямых в пространстве.

Чтобы две прямые были параллельны необходимо и достаточно, чтобы направляющие векторы этих прямых были коллинеарны, т.е. их соответствующие координаты были пропорциональны: .

Чтобы две прямые были перпендикулярны необходимо и достаточно, чтобы направляющие векторы этих прямых были перпендикулярны, т.е. косинус угла между ними равен нулю:

Условие, при котором две прямые лежат в одной плоскости.

П усть прямые L₁ и L₂ заданы каноническими уравнениями: , где и . Тогда

. Прямые L₁ и L₂ лежат в одной пл-ти, если векторы , и компланарны. Следовательно, получаем условие:

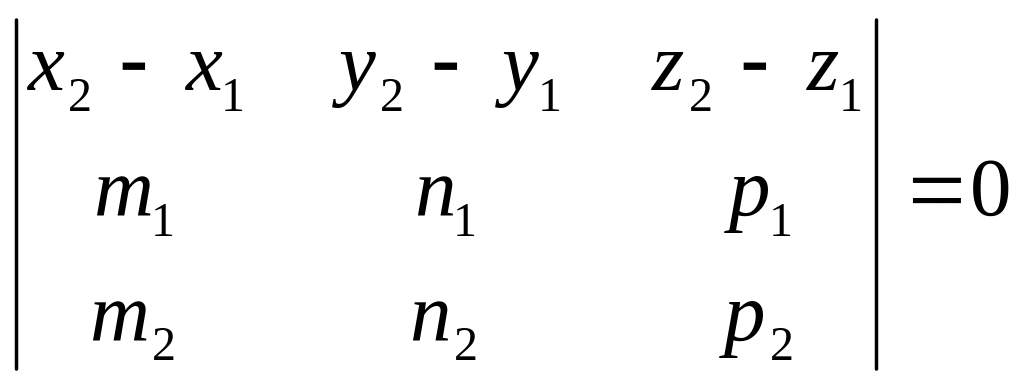
Угол между прямой и плоскостью.

Определение. Углом между прямой и плоскостью называется любой угол между прямой и ее проекцией на эту плоскость.







Пусть плоскость задана уравнением , а прямая - . Из геометрических соображений (см. рис.) видно, что искомый угол  = 90⁰ - , где  - угол между векторами и . Этот угол может быть найден по формуле:



В координатной форме:

Условия параллельности и перпендикулярности прямой и плоскости в пространстве.

Для того, чтобы прямая и плоскость были параллельны, необходимо и достаточно, чтобы вектор нормали к плоскости и направляющий вектор прямой были перпендикулярны. Для этого необходимо, чтобы их скалярное произведение было равно нулю.

Для того, чтобы прямая и плоскость были перпендикулярны, необходимо и достаточно, чтобы вектор нормали к плоскости и направляющий вектор прямой были коллинеарны. Это условие выполняется, если векторное произведение этих векторов было равно нулю.

Пересечение прямой с плоскостью. Условие принадлежности прямой плоскости.

Пусть требуется найти точку пересечения прямой с пл-тью .

Для этого перепишем уравнение прямой в параметрическом виде:

Подставляя эти выражения для x,y и z в уравнение пл-ти, получаем или .

Если прямая L не параллельна пл-ти, т.е. , то из равенства находим значение t: .

Подставляя найденное значение t в параметрические ур-ния прямой, найдем координаты точки пересечения прямой с плоскостью.

Случаи, когда :

1. если 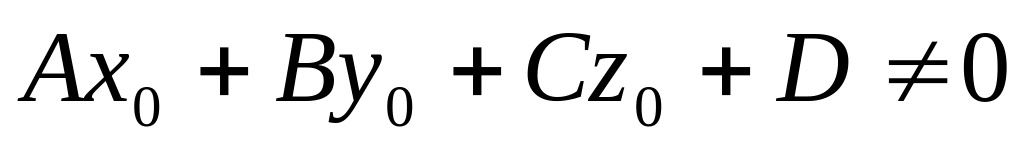, то прямая L параллельна пл-ти и пересекать ее не будет.

2. если , то t – любое, следовательно, прямая принадлежит пл-ти.

16