Аналитическая геометрия. Системы координат.

Любая точка на плоскости может быть однозначно определена при помощи различных координатных систем, выбор которых определяется различными факторами.

Способ задания начальных условий для решения какой – либо конкретной технической задачи может определить выбор той или иной системы координат. Для удобства проведения вычислений часто предпочтительнее использовать системы координат, отличные от декартовой прямоугольной системы. Кроме того, наглядность представления окончательного ответа зачастую тоже сильно зависит от выбора системы координат.

Определение. Под системой координат на плоскости понимают способ, позволяющий численно описать положение точки плоскости.

Прямоугольная (декартова) система координат.

П рямоуголная система координат задается двумя взаимно перпендикулярными прямыми – осями, на каждой из которых выбрано положительное направление и задан единичный отрезок. Ось ОХ наз. осью абсцисс, ось ОУ – осью ординат. Единичные векторы обозначают i и j ( ). Вектор ОМ называют радиусом-вектором точки М. Координатами точки М в системе ОХУ называются координаты радиуса-вектора ОМ.

Полярная система координат.

Полярная система координат задается точкой О называемой полюсом, а лучом l – полярной осью.

С уть задания какой- либо системы координат на плоскости состоит в том, чтобы каждой точке плоскости поставить в соответствие пару действительных чисел, определяющих положение этой точки на плоскости. В случае полярной системы координат роль этих чисел играют расстояние точки от полюса и угол между полярной осью и радиус– вектором этой точки. Этот угол  называется полярным углом.

Числа r и  называются полярными координатами точки М, пишут М(r; ), при этом r называется полярным радиусом,  - полярным углом.

Можно установить связь между полярной системой координат и декартовой прямоугольной системой, если поместить начало декартовой прямоугольной системы в полюс, а полярную ось направить вдоль положительного направления оси Ох.

Т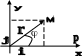 огда координаты произвольной точки в двух различных системах координат связываются соотношениями:

x = rcos; y = rsin; x² + y² = r²

П

r =

олярные же координаты точки М выражаются через ее декартовы координаты такими формулами:

. Определяя величину , следует установить четверть, в которой лежит искомый угол, и учесть, что .

Цилиндрическая и сферическая системы координат.

Как и на плоскости, в пространстве положение любой точки может быть определено тремя координатами в различных системах координат, отличных от декартовой прямоугольной системы. Цилиндрическая и сферическая системы координат являются обобщением для пространства полярной системы координат.

Введем в пространстве точку О и луч l, выходящий из точки О, а также вектор . Через точку О можно провести единственную плоскость, перпендикулярную вектору нормали .

Для введения соответствия между цилиндрической, сферической и декартовой прямоугольной системами координат точку О совмещяют с началом декартовой прямоугольной системы координат, луч l – с положительным направлением оси х, вектор нормали – с осью z.

z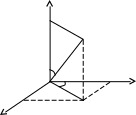

М



 h

0  x

r

M₁

y

ОМ₁ = r; MM₁ = h;

Цилиндрическая и сферическая системы координат используются в тех случаях, когда уравнение кривой или поверхности в декартовой прямоугольной системе координат выглядят достаточно сложно, и операции с таким уравнением представляются трудоемкими. Представление уравнений в цилиндрической и сферической системе позволяет значительно упростить вычисления.

Если из точки М опустить перпендикуляр ММ₁ на плоскость, то точка М₁ будет иметь на плоскости полярные координаты (r, ).

Определение. Цилиндрическими координатами точки М называются числа (r, , h), которые определяют положение точки М в пространстве.

Определение. Сферическими координатами точки М называются числа (r,,), где  - угол между  и нормалью.