В ортогональном базисе

Если имеется СЛО, ОНБ и матрица в этом базисе. Тогда справедлива теорема 2: симметричный ЛО имеет ОНБ, состоящий из его собственных векторов и все его собственные значения действительны.

Введем условные обозначения: - собственное значение, а – собственный вектор СЛО

Доказательство:

На этом вторая часть теоремы доказана. Перейдем к первой:

Пусть теперь так: - собственное значение СЛО, а - его собственный вектор. Используем метод мат. индукции (от частного к общему).

1. База: пусть пространство одномерно. В таком случае для элемента справедливо равенство:

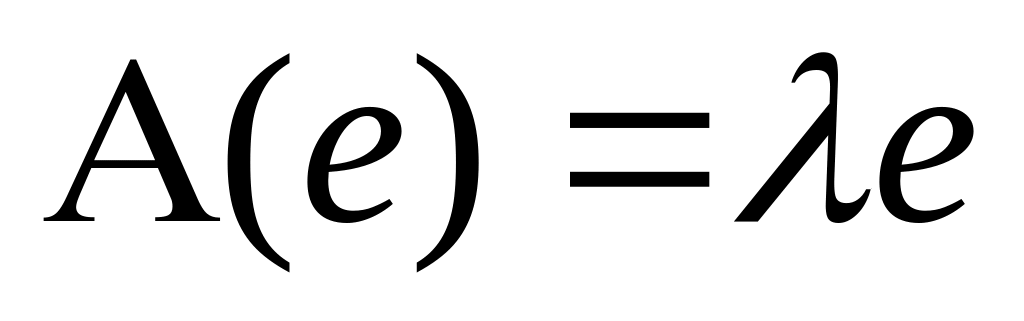
2. Шаг:

-ИПП, значит - ИПП с размерностью имеется ОНБ: тогда 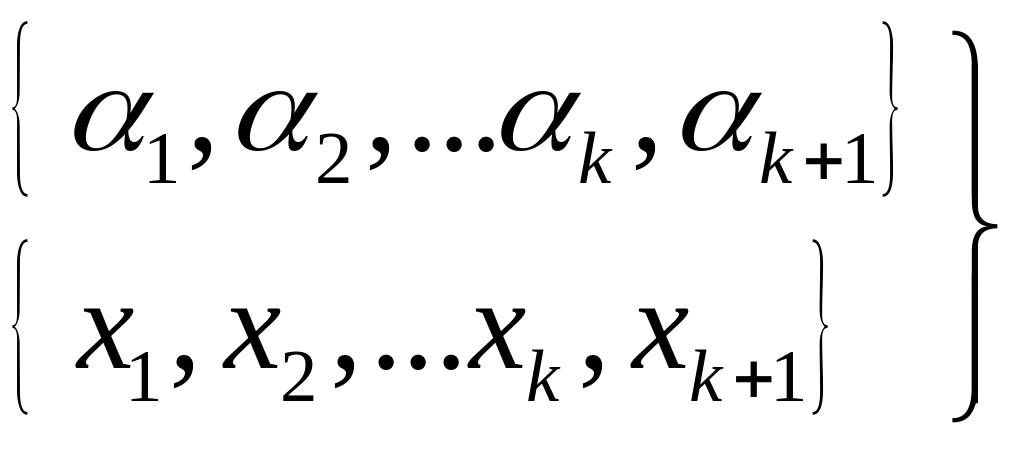-ОНБ во всем линейном пространстве

Отметим, что если - ОНБ у собственных векторов с собственными значениями , то

(так как матрица с симметричный ЛО в базисе будет - диагональной матрицей.

Итак, доказано следующее:

Теорема 3: Любой симметричный ЛО имеет ортонормированный базис, в котором его матрица диагональна.

Если – матрица перехода в базисе собственных векторов симметричного линейного оператора , то так как базис у собственных векторов – ОНБ, то имеет место равенство .

Определение: матрица называется симметричной, если .

Теорема 4: Симметричный ЛО в линейном ОНБ имеет симметричную матрицу.

Доказательство:

Так как в Евклидовом пространстве:

, тогда , т.е. из теоремы 3 и 4 легко следует.

Теорема 5: Для всякой симметричной матрицы А существует ортонормированная матрица С такая, что матрица является диагональной матрицей. Матрица С является матрицей перехода к базису собственных векторов симметричного матричного оператора , имеется матрица A (т.е. ).

§52 Билинейный функционал. Квадратичная форма. Приведение квадратичной формы к каноническому виду

52.1 Определение билинейного функционала

Определение: Билинейный функционал (БФ) – это некоторое соответствие, переводящие, например, любую точку в Декартовых координатах (X,Y) в некоторую другую точку. БФ обладает свойствами:

1.

2.

3.

52.2 Общий вид билинейного функционала

Пусть имеется базис из элементов . Тогда:

, где

Это и есть общий вид БФ а матрица называется матрицей билинейного функционала.

52.3 Матрица билинейного функционала и её преобразования при переходе к другому базису

Имеется два базиса: и , а матрица C переводит первый базис во второй. Зададим составляющие базиса следующим образом:

и

Найдем БФ между представленными выше элементами:

Таким образом, матрица БФ преобразовывает так: .

Определение: БФ симметричен, если для любых элементов x и y справедливо равенство:

Такой БФ имеет симметричную матрицу.

Определение: БФ имеет канонический вид, если его матрица приведена к диагональному виду.

Теорема: для любого симметричного БФ существует ОНБ, в котором он имеет диагональную матрицу.

Доказательство:

Так как симметричный БФ имеет симметричную матрицу так, что по теореме 5, существует такая матрица диагональная и его общий вид будет следующим . Продолжение доказательства в след. пункте.