12.3. Плоскость. Основные задачи

Угол между двумя плоскостями. Условия параллельности и перпендикулярности двух плоскостей

Пусть заданы две плоскости Q₁ и Q₂:

A₁x + B₁y + C₁z + D₁ = 0,

А₂х + В₂у + C₂z + D₂ = 0.

Под углом между плоскостями Q₁ и Q₂ понимается один из двугран­ных углов, образованных этими плоскостями.

Угол φ между нормальными векторами = (A₁;B₁;C) и = (А₂;В₂; С₂) плоскостей Q₁ и Q₂ равен одному из этих углов (см. рис. 72). Поэтому или

Для нахождения острого угла следует взять модуль правой части.

Рис. 72. Рис. 73.

Если плоскости Q₁ и Q₂ перпендикулярны (см. рис. 73, а), то тако­вы же их нормали, т. е. (и наоборот). Но тогда · = 0, т. е. А₁А₂ + В₁В₂ + С₁С₂ = 0. Полученное равенство есть условие перпендику­лярности двух плоскостей Q₁ и Q₂.

Если плоскости Q₁ и Q₂ параллельны (см. рис. 73, б), то будут па­раллельны и их нормали и (и наоборот). Но тогда, как известно, координаты векторов пропорциональны: Это и есть условие параллельности двух плоскостей Q₁ и Q₂.

Расстояние от точки до плоскости

Пусть задана точка М₀(х₀;у₀; z₀) и плоскость Q своим уравнением Ах + By + Cz + D = 0. Расстояние d от точки М₀ до плоскости Q находится по формуле

Вывод этой формулы такой же, как вывод формулы расстояния от точки М₀(х₀;у₀) до прямой Ах + By + С = 0 (см. с. 61).

Расстояние d от точки М₀ до плоскости Q равно модулю проекции вектора , где M₁(x₁;y₁;z₁) — произвольная точка плоскости Q,.на направление нормального вектора = (А; В; С) (см. рис. 74). Следовательно,

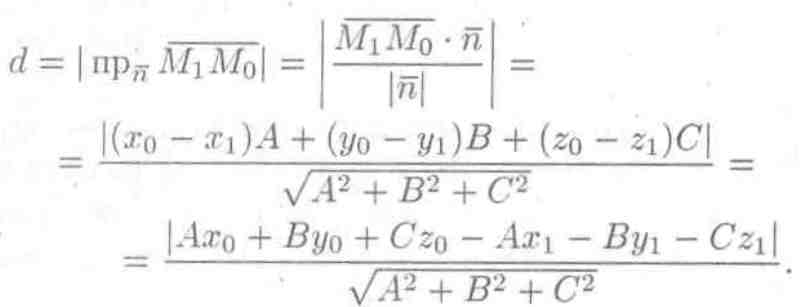
Рис. 74!

А так как точка M₁(x₁;y₁;z₁) принадлежит плоскости Q, то Ax₁+By₁+Cz_l+D = 0, т.е. D = -Ax₁ – Ву₁ – Сz₁.Поэтому . Отметим, что если плоскость Q задана уравнением xcos α + у cos β + z cos γ -р = 0, то расстояние от точки М₀(х₀;у₀; z₀) до плоскости Q может быть найдено по формуле

d = |x₀ cos α + ;y₀ cosβ + z₀ cosγ - р|.

Уравнения прямой в пространстве

Векторное уравнение прямой

Положение прямой в пространстве вполне определено, если задать какую-либо точку М₀ на прямой и вектор , параллельный этой пря­мой. Вектор называется направляющим вектором прямой. Пусть прямая L задана, ее точкой М₀(хо; у₀; z₀) и направляющим вектором = (т;п;р). Возьмем на прямой L произвольную точку M(x;y;z). Обозначим радиус-векторы точек M₀ и М соответственно через и . Очевидно, что три вектора , и связаны соотношением

= + (12.10)

Вектор , лежащий на прямой L, параллелен направляющему вектору , поэтому = t , где t — скалярный множитель, называемый параме­тром, может принимать различные значения в за­висимости от положения точки М на прямой (см. рис. 75).

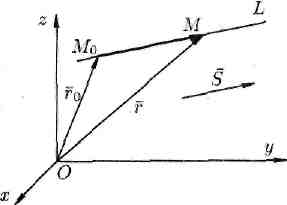
Рис. 75.

Уравнение (12.10) можно записать в виде

= + t (12.11)

Полученное уравнение называется векторным уравнением прямой.

Параметрические уравнения прямой

Замечая, что = (x;y;z), = (х₀;у₀;z₀), t = (tm;tn;tp), уравне­ние (12.11) можно записать в виде

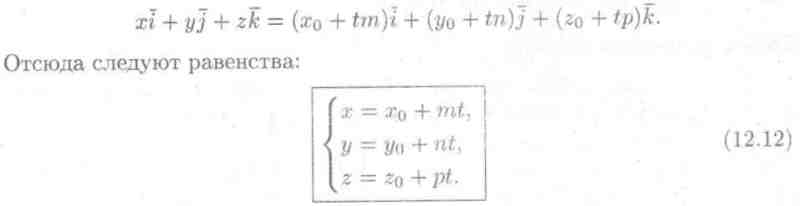
Они называются параметрическими уравнениями прямой в пространстве.

Канонические уравнения прямой

Пусть = (m;n;p) — направляющий вектор прямой L и M₀(x₀; y₀;z₀) - точка, лежащая на этой прямой. Вектор , соединяющий точку M₀ с произвольной точкой М(х; у; z) прямой L, параллелен вектору . Поэтому координаты вектора = (х - х₀; у – у₀; z - z₀) и вектора = (m;n;p) пропорциональны:

(12.13)

Уравнения (12.13) называются каноническими уравнениями прямой в пространстве.

Замечания: 1) Уравнения (12.13) можно было бы получить сразу из па­раметрических уравнений прямой (12.12), исключив параметр t. Из урав­нений (12.12) находим

= t