27. Абсолютное, относительное и переносное движение точки:

Рассмотрим сложное движение т. М, перемещающейся по отношению к подвижной системе отсчёта Охуz, которая в свою очередь движется отн-но другой системы отсчёта О1х1у1z1, условно называемой неподвижной. Д-ние, совершаемое т. М по отношению к подвижным осям координат, наз-ся относительным. Д-ние, совершаемое подвижной системой отсчёта Охуz по отношению к неподвижной системе отсчёта О1х1у1z1, наз-ся переносным. Д-ние, совершаемое точкой по отношению к неподвижной системе отсчёта О1х1у1z1, наз-ся абсолютным или сложным.

28. Сложение скоростей при сложном движении точки:

Пусть т. М совершает сложное Д-ние. V_а =V_отн.+ V_пер.

Теорема о сложении ск-тей: при сложном Д-нии абсолютная ск-ть т-ки равна геометрической сумме относительной и переносной ск-тей. Р.1б-параллелограмм ск-тей. Если угол м/у направлениями векторов V_отн. и V_пер равен α, то по модулю: V_а=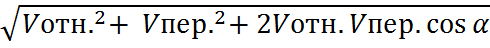

29. Сложение ускорений при сложном движении точки. Случай поступательного пере­носного движения:

Найдем зависимость между абсолютным, относительным и переносным ускорениями точки. Из равенства V_а =V_отн.+ V_пер получаем: W_A = = + .

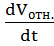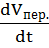Пусть положение движущейся точки М в подвижных осях Oxyz определяется её координатами x,y,z (рис.а).

V_отн.=ẋi+ẏj+ẑk; W_отн.= x’’i+y’’j+z’’k

i, j,k— единичные векторы (орты) осей Oxyz.

Сложение ускорений при поступательном переносном движении. Если подвижная система отсчёта Oxyz перемещается по отношению к неподвижной O1x1y1z1 поступательно, то при любом положении т. М будет V_пер= V_о; W_пер.= W_о, где V_о и W_о-ск-ть и ускорение начала О. При поступательном движении осей Oxyz их орты, перемещаясь параллельно самим себе, остаются постоянными. 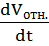= x’’i+y’’j+z’’k= W_отн; =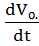 = W_о = W_пер.; W_А= W_отн.+ W_пер.

При поступательном переносном движении абсолютное ускорение точки равно геометрической сумме относительного и переносного ускорений.

30. Теорема Кориолиса. Ускорение Кориолиса:

Теорема Кориолиса: абсолютное ускорение точки равно геометрической сумме 3-ёх ускорений: относительного, переносного и кориолисова. Сложное Д-ние=переносное Д-ние+относительное Д-ние: ; ;

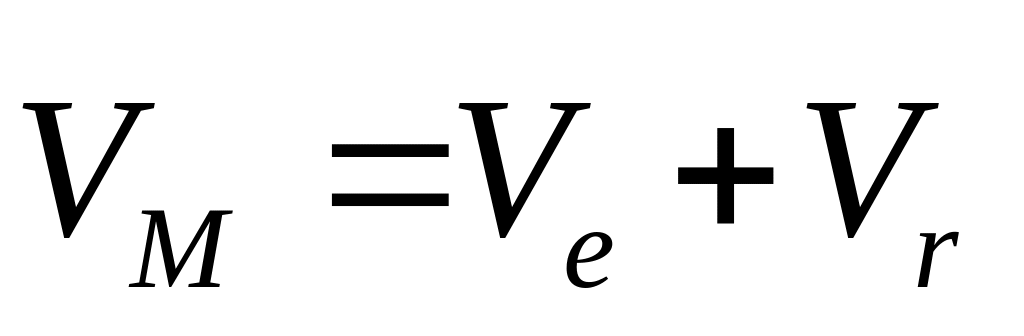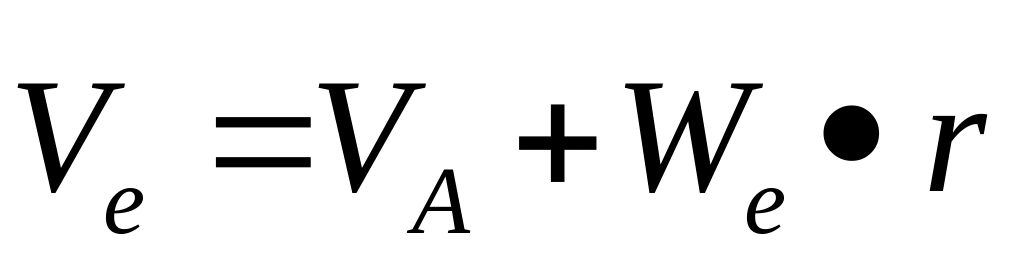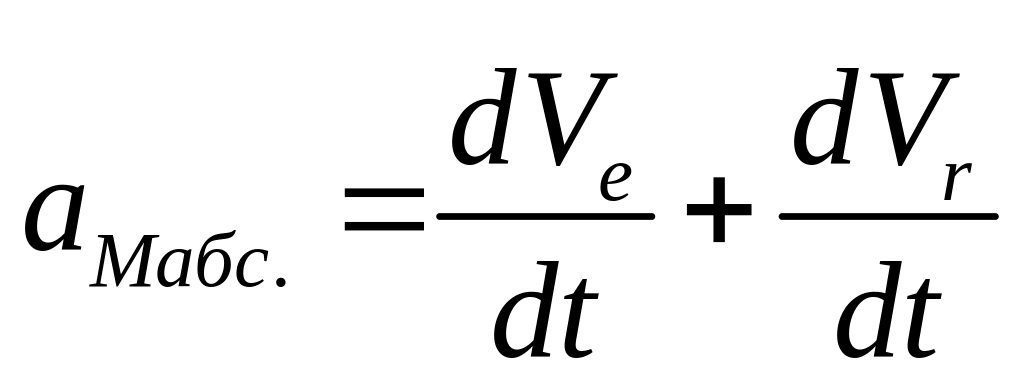
Рассмотрим 2 случая:

1-переносное Д-ние поступательное: 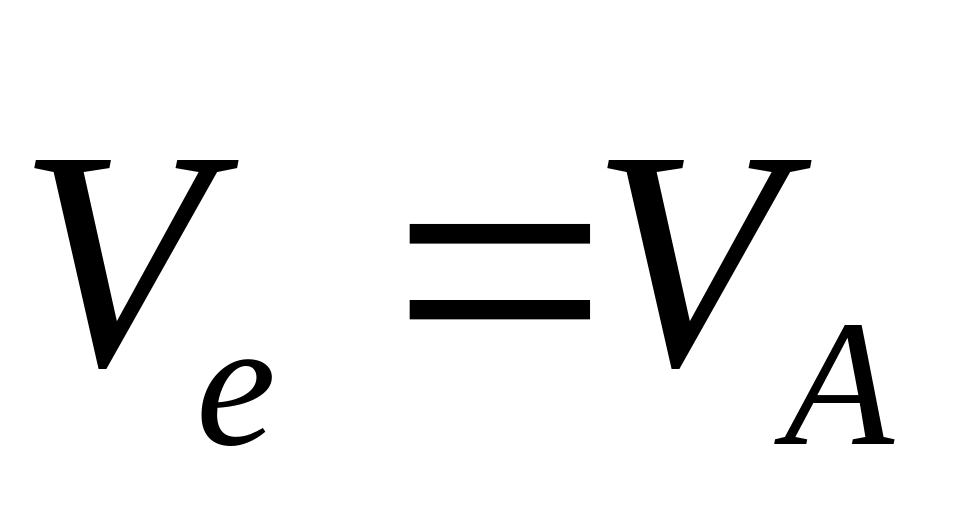(т.к.W=0); ; ; 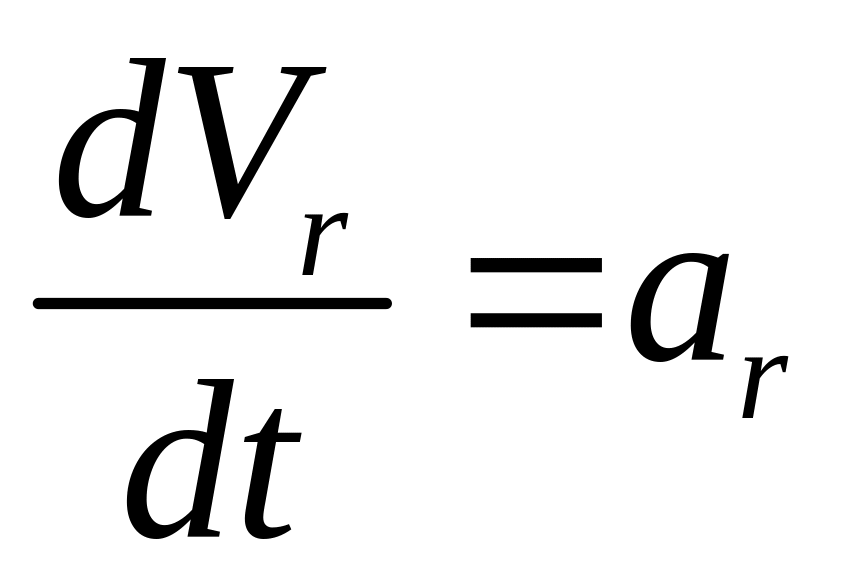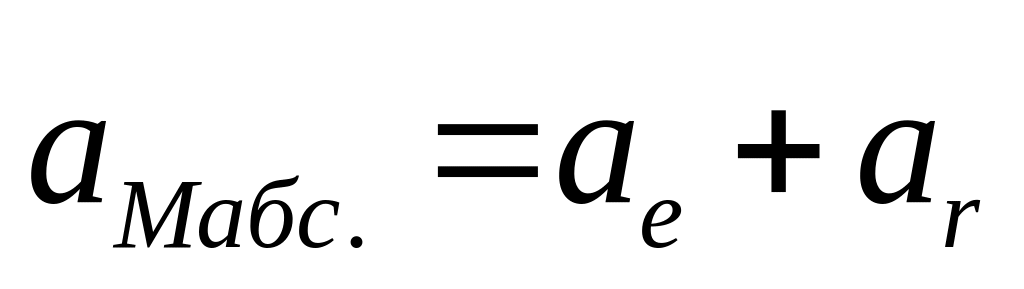При поступательном Д-нии абсолютное ускорение точки =геометрической сумме переносного и относительного ускорений.

2-Рассмотрим непоступательное переносное Д-ние: 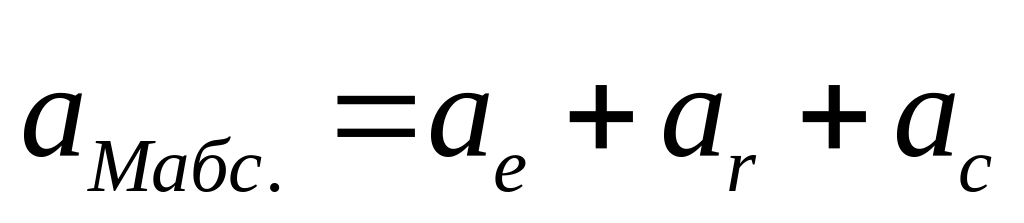; В случае непоступательного переносного Д-ния абсолютное ускорение точки = геометрической сумме переносного, относительного и кориолисова ускорений.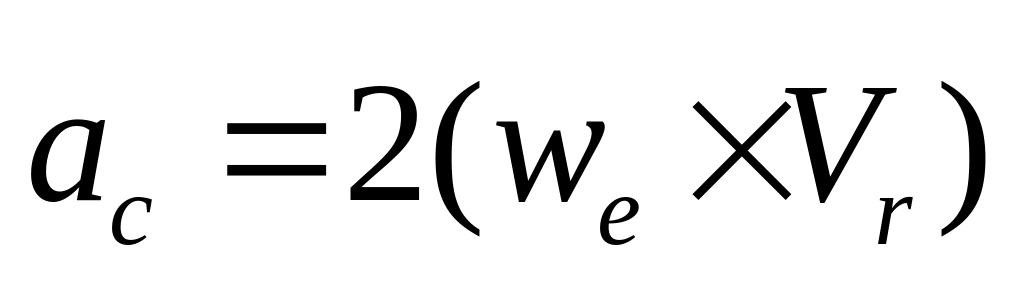

31. Опред-ние направления и модуля ускорения Кориолиса. Случаи, когда ускорение Кориолиса равно нулю:

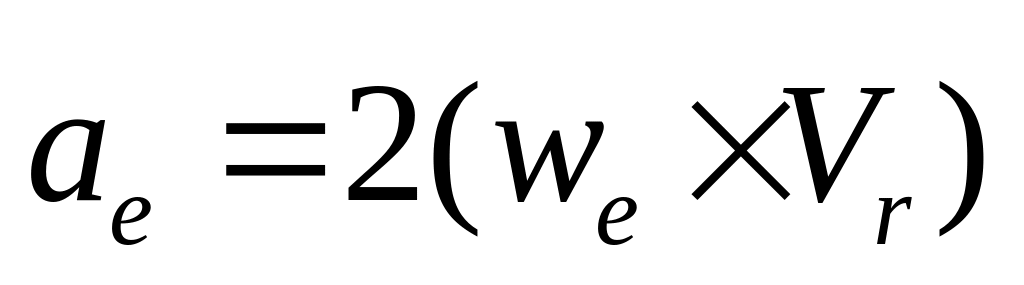
Ускорение Кориолиса хар-ет изменение модуля и направления переносного ускорения т-и М’ вследствие её относительного Д-ния.

a_c=2W_eV_rsin α, где α-угол м/у направлением α= 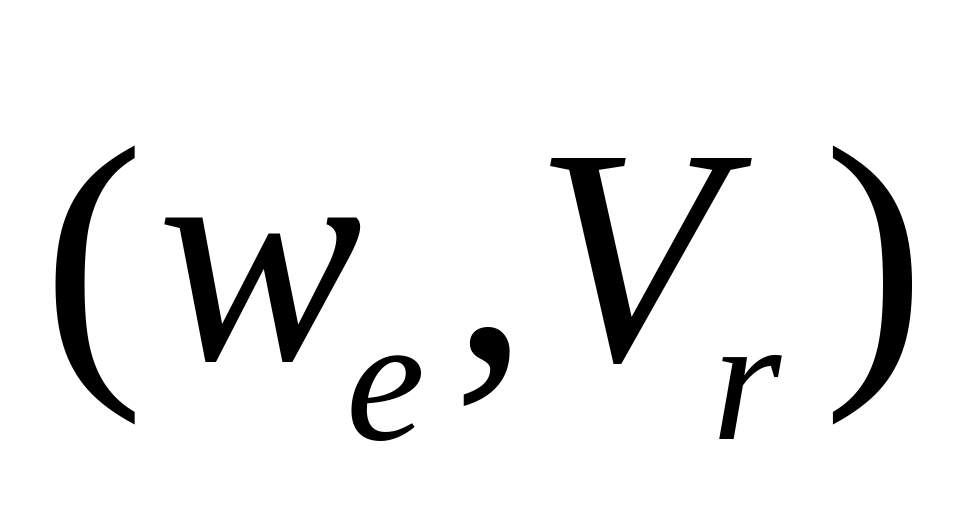. Он может быть как острым, так и тупым.

Ускорение Кориолиса =0 в 3-ёх случаях:

1.W_e=0; 2. V_r=0; 3. α=0 или α=180⁰