53. Понятие механической системы (системы материальных точек). Внешние и внутренние силы:

Механической системой наз-ся такая их совокупность, в которой положение или движение каждой точки (или тела) зависит от положения и движения все остальных.

Классическим примером механической системы является солнечная система, в которой все тела связаны силами взаимного притяжения. МС: 1. МС свободных т-ек или тел (прим. Солнечная сист.).2. МС несвободных т-ек или тел (прим. двигатели внутреннего сгорания).

Внешними наз-ся силы, действующие на точки системы со стороны точек и тел, не входящих в состав данной системы. Внутренними наз-ся силы, действующие на точки системы со стороны других точек или тел этой же системы. Внешние силы обозначаются F^e, утренние-Fⁱ. Внешние и внутренние силы могут быть или активными, или р-циями связи. Разделение сил на внешние и внутренние является условным и зависит от того, Д-ние какой системы тел мы рассматриваем. Внутренние силы обладают следующими св-вами:1. Геометрическая сумма (главный вектор) всех внутренних сил системы =0. 2. Сумма мом-тов (главный мом-т) всех внутренних сил системы отн-но любого центра или оси =0.

54. Масса механической системы. Центр масс механической системы:

Движение системы, кроме действующих сил, зависит также от ее суммарной массы и распределения масс. Масса системы равна арифметической сумме масс всех точек или тел, образующих систему: М=

В однородном поле тяжести, для которого g= const, вес любой частицы тела будет пропорционален ее массе. Поэтому о распределении масс в теле можно судить по положению его центра тяжести.

Геометрическая точка C, координаты которой определяются

формулами 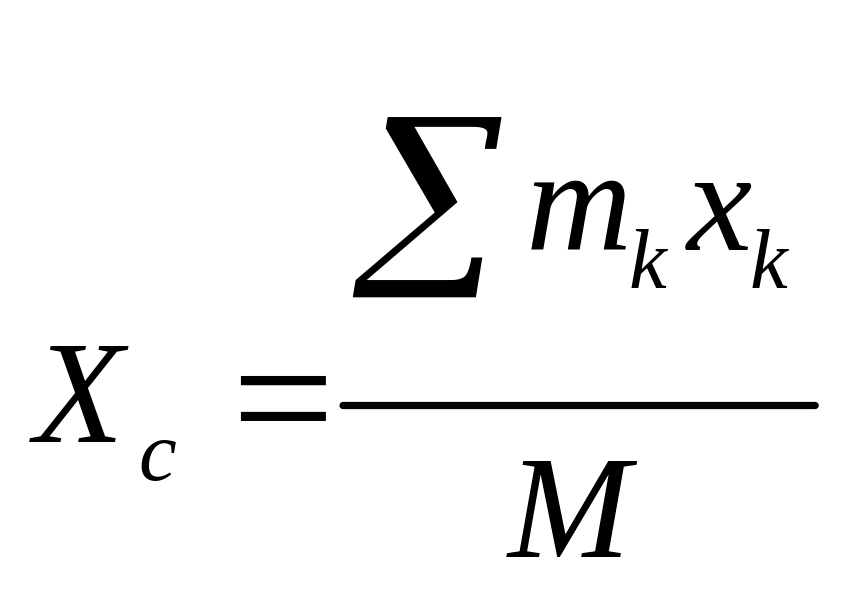, , 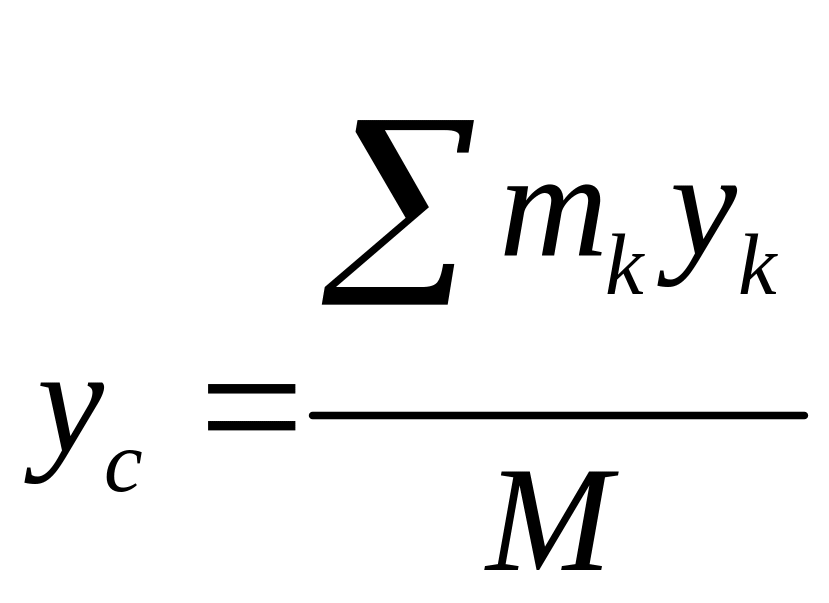, называетcя центром масс МС или центром инерции МС.

Если положение центра масс определять его радиусом-вектором, r₀, то

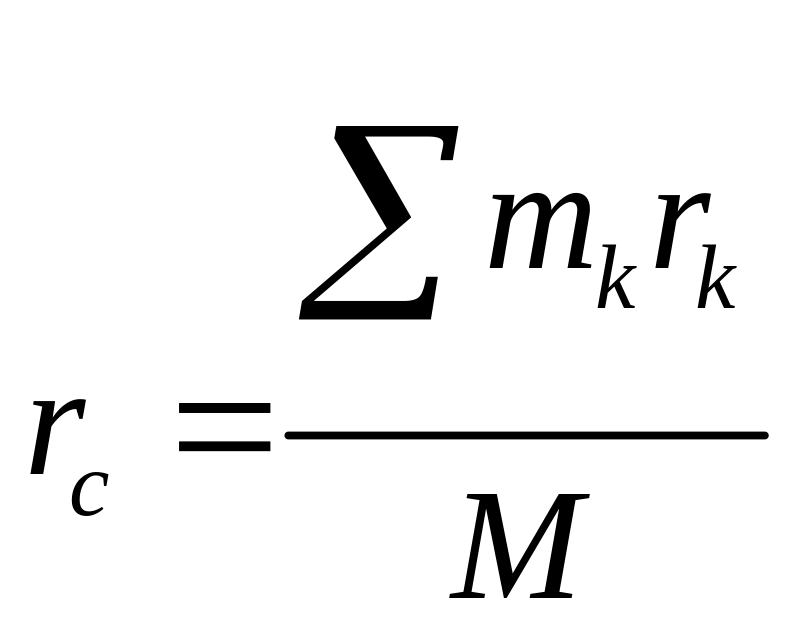
где r_k— радиусы-векторы точек, образующих систему.

Хотя положение центра масс совпадает с положением центра тяжести тела, находящегося в однородном поле тяжести, понятия эти не являются тождественными. Понятие о центре тяжести, как о точке, через которую проходит линия действия равнодействующей сил тя­жести, по существу имеет смысл только для твердого тела, находя­щегося в однородном поле тяжести. Понятие же о центре масс, как о характеристике распределения масс в системе, имеет смысл для любой системы материальных точек или тел, причем это понятие сохраняет свой смысл независимо от того, находится ли данная си­стема под действием каких-нибудь сил или нет.

55-56. Моменты инерции твердых тел. Моменты инерции твердых тел относительно параллельных осей. Теорема Гюйгенса:

Мом-том инерции тела (системы) отн-но данной оси Oz (или осевым мом-том инерции) наз-ся скалярная величина, равная сумме произведений масс всех точек тела (системы) на квадраты их расстояний от этой оси. J_Z= 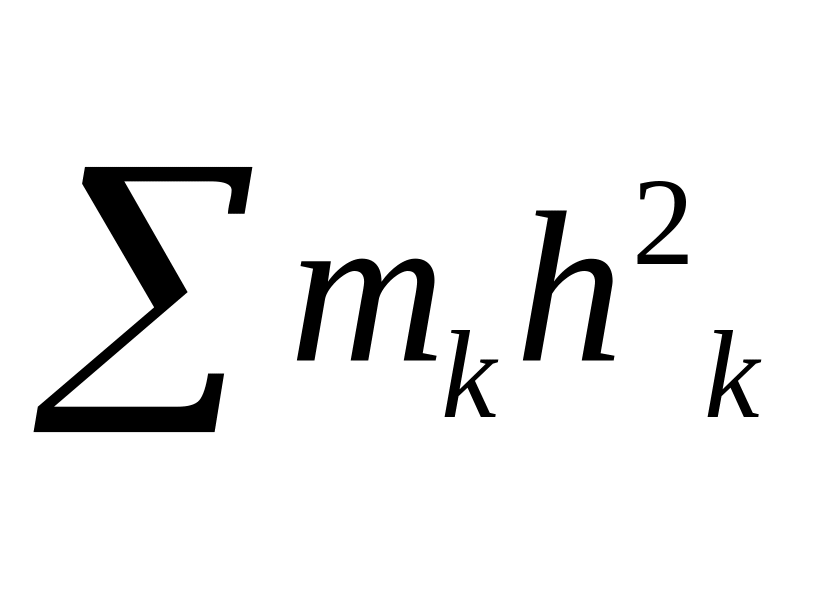Из определения следует, что J_Z>0. Для тонкого однородного стержня: J_А= ML². Для круглой однородной пластины или цилиндра: J_с= MR². Для тонкого круглого однородного кольца: J_с=MR²

Теорема Гюйгенса: момент инерции тела относительно данной оси равен моменту инерции относительно оси, ей параллельной, проходящей через центр масс тела, сложенному с произведением массы всего тела на квадрат расстояния между осями.J_OZ= J_CZ’+Md².

Из формулы следует, что Joz>J_CZ’Следовательно, из всех осей данного направления наименьший момент инерции будет отно­сительно той оси, котороя проходит через центр масс.

Теорема Гюйгенса позволяет найти момент инерции тела отно­сительно данной оси O_z1 и в том случае, когда известен его момент инерции относительно любой оси A_Z2 параллельной данной.

При этом надо знать расстояния d₁ и d₂ каждой из этих осей от центра масс тела. Тогда, зная J_AZ2 и d₂ мы по формуле определяем Jcz’, а затем по той же формуле находим искомый момент инерции Joz₁.