3.3. Оценка интеграла. Теорема о среднем. Среднее значение функции.

I. Оценка интеграла. Укажем границы, между которыми наверняка заключено значение интеграла.

Теорема VI (об оценке определенного интеграла). Значение определенного интеграла заключено между произведениями наименьшего и наибольшего значений подынтегральной функции на длину интервала интегрирования, т. е.

где т и М — соответственно наименьшее и наибольшее значения функции интервале :

Доказательство. Возьмем две функции и . Первая из них в интервале неотрицательна, вторая неположительна. Значит, по теореме V¹⁾

и

а по теореме I

и

откуда в силу того, что

и

что и требовалось доказать.

Г

Рис.6

еометрический смысл этих неравенств таков: площадь криволинейной трапеции больше площади прямоугольника с основанием, равной основанию трапеции, и высотой, равной наименьшей ординате трапеции, и меньше площади прямоугольника с тем же основанием и высотой, равной наибольшей ординате трапеции (рис. 6).

Находя границы для интеграла, мы, как говорят, производим его оценку. Может случиться, что весьма трудно или даже невозможно найти точное значение интеграла, а оценивая его, мы узнаем, хотя бы грубо, приближенное его значение. С такого, рода оценками приходится довольно часто встречаться в математике.

Указанные в теореме VI границы для интеграла тем более точны, чем короче интервал интегрирования и чем меньше линия отличается по положению от прямой, параллельной оси Ох.

Пример. Оценим интеграл

Легко проверить, что подынтегральная функция в интервале убывает и, следовательно,

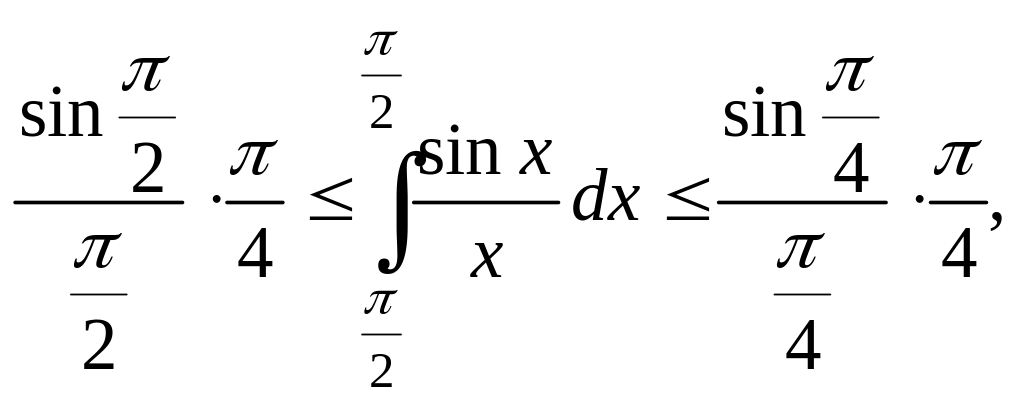
т. е.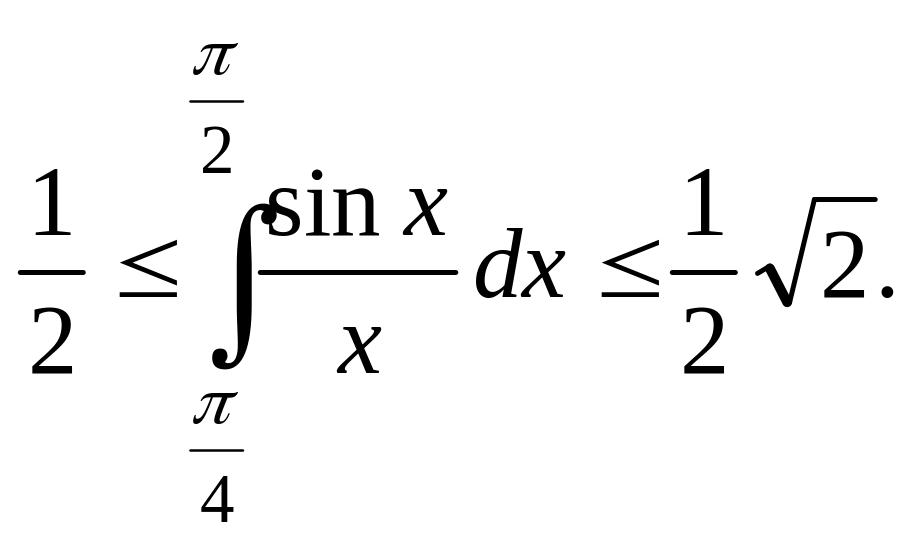

Таким образом, интеграл заключен между 0,5 и 0,71, что дает нам право считать его равным 0,6 с точностью до 0,1. Более точные приемы показывают, что приближенно он равен 0,62.

II. Обобщение теоремы об оценке интеграла. Интегрирование неравенств.

Справедлива следующая более общая теорема, чем теорема VI:

Теорема VII. Если в каждой точке х интервала

то

Это значит, что неравенство между функциями влечет неравенство того же смысла между их определенными интегралами, или, говоря коротко, неравенства можно интегрировать¹¹..

На доказательстве и геометрическом смысле теоремы останавливаться не будем, так как они вполне подобны предыдущим.

В частном случае, когда тождественно равно М, а тождественно равно т, получаем теорему VI.

III. Теорема о среднем.

Определенный интеграл обладает следующим важным свойством:

Теорема VIII (о среднем). Внутри интервала интегрирования существует, по меньшей мере, одно значение для которого

. (*)

Доказательство. В силу теоремы VI имеем:

и, значит,

где  — некоторое число, заключенное между наименьшим (т) и наибольшим (М) значениями функции в интервале , т. е. . Но , будучи непрерывной функцией, обязательно принимает, по меньшей мере, один раз каждое значение, лежащее между т и М. Следовательно, при некотором получит значение, равное , т. е. (см. рис. 6), что и требовалось доказать.

Из равенства (*) находим:

Эта формула позволяет теорему о среднем высказать в такой форме:

Определенный интеграл от непрерывной функции, равен произведению значения этой функции в некоторой промежуточной точке интервала интегрирования, на длину интервала.

Дадим наглядное пояснение теоремы. При движении прямой, параллельной оси Ох (рис. 6), вверх от положения ВС площадь прямоугольника АВСК будет непрерывно возрастать от величины, меньшей площади трапеции, до величины, большей ее. Очевидно, при некотором промежуточном положении прямой — обозначим его через FG — площадь прямоугольника AFGK окажется в точности равной площади трапеции s. Так как при этом движении прямая постоянно пересекает линию, ограничивающую трапецию, то и в положении FG найдется одна или несколько (на рис. 7 две) точек пересечения Q; абсцисса любой точки пересечения и будет требуемым по теореме значением .

Е

Рис.7

сли трапецию ограничивает прямая линия, то ; отрезок PQ будет при этом средней линией прямолинейной трапеции.

IV. Среднее арифметическое значение функции. Значение , находимое по теореме о среднем, называется средним арифметическим значением функции в интервале .

Определение. Средним арифметическим значением непрерывной функции в интервале называется отношение определенного интеграла от этой функции к длине интервала:

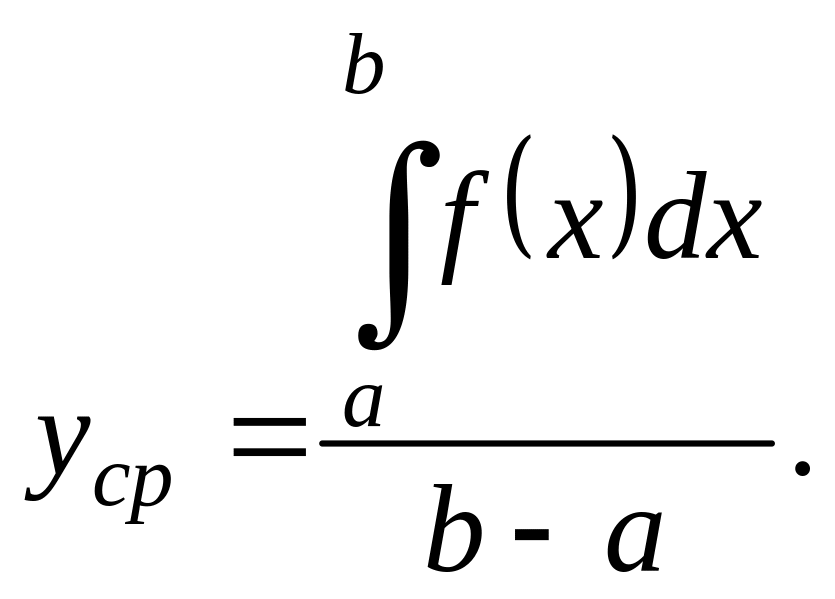
Приведем некоторые соображения в обоснование этого определения.

Пусть некоторая величина у принимает п значений: Средним арифметическим значением этой величины называется частное . Так если температура воздуха в течение суток измеряется через каждый час, то средней температурой будет частное от деления суммы всех наблюденных температур на 24.

Но представим себе теперь, что величина изменяется непрерывно (например, температура воздуха известна в любой момент суток) и мы хотим как-то в среднем охарактеризовать всю совокупность ее значений. Как в этом случае следует определить среднюю температуру воздуха, принимая во внимание всю известную совокупность значений температуры? Вообще, что следует принять в качестве среднего значения непрерывной функции в некотором интервале ?

Разобьем интервал на п равных частей с помощью точек и возьмем значения функции в этих n точках:

Значениями нашей функции во всех остальных точках интервала пока пренебрежем. Возьмем среднее арифметическое указанных значений:

Ясно, что чем больше п, тем больше значений функции учитывается при отыскании среднего значения, и поэтому естественно за среднее значение функции принять предел, к которому стремится при . Найдем этот предел.

Умножив и разделив выражение для на , получим:

но так как то

откуда, переходя к пределу, получаем указанное нами выше выражение для среднего значения:

На основании теоремы о среднем (теорема VIII) мы заключаем, что , где , т. е. что среднее значение непрерывной функции в интервале всегда (если только функция не постоянная) меньше некоторых ее значений, больше других ее значений и равно по меньшей мере одному ее значению.

Понятие среднего значения функции очень употребительно в технике. Многие величины часто характеризуются своими средними значениями; таковы, например, давление пара, сила и напряжение переменного тока, скорость химической реакции и т. п.