2.4. Основные теоретические вопросы и методические

рекомендации для выполнения четвертого задания

1. Проверка гипотезы о нормальном распределении

генеральной совокупности по критерию Пирсона

Многие задачи статистики решаются при неизвестном законе распределения генеральной совокупности. Возникает задача выбора модели закона распределения и соответственно проверки, на сколько выбранная модель согласуется с выборкой. Критерий, с помощью которого проверяется нулевая гипотеза о виде закона распределения, называется критерием согласия. Критериев в статистике достаточно много. Рассмотрим один из них – критерий Пирсона.

Пусть эмпирическое распределение задано в виде последовательности равноотстоящих вариант и соответствующих им частот:

хi	х1	х2	…	хv
ni	n1	n2	…	nv

Требуется, используя критерий Пирсона, проверить гипотезу о том, что генеральная совокупность Х распределена нормально.

Правило 1. Для того чтобы при заданном уровне значимости α проверить гипотезу о нормальном распределении генеральной совокупности, нужно:

1. Вычислить непосредственно (при малом числе наблюдений) или упрощенным методом (при большом числе наблюдений), например методом произведений или сумм, выборочную среднюю и выборочное среднее квадратическое отклонение σ_В.

2. Вычислить теоретические частоты

,

где n – объем выборки, h – шаг,

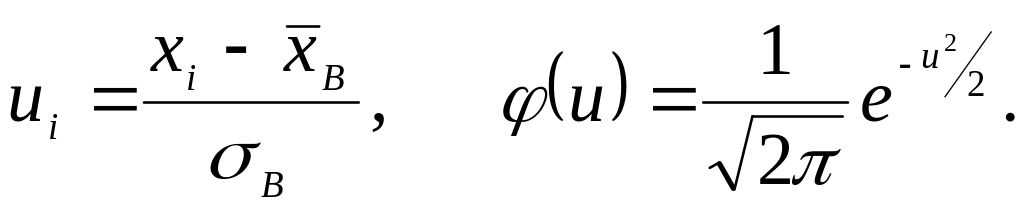
3. Сравнить эмпирические и теоретические частоты с помощью критерия Пирсона. Для этого:

а) составляют расчетную таблицу, по которой находят наблюдаемое значение критерия

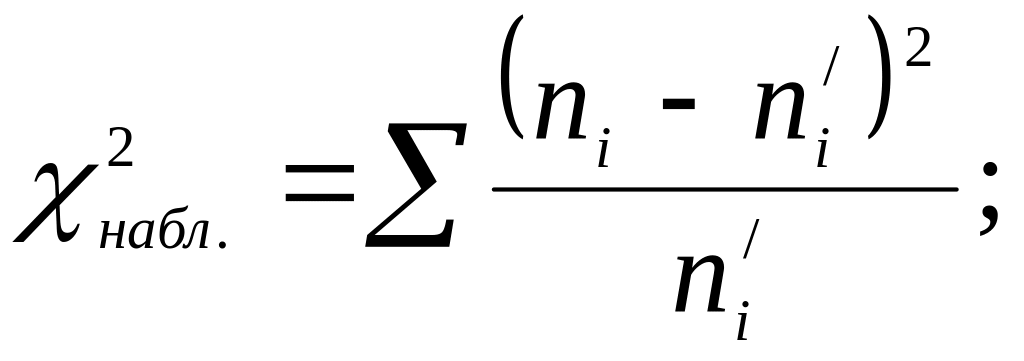
б) по таблице критических точек распределения χ², по заданному уровню значимости α и числу степеней свободы k = v – 3 (v – число групп выборки) находят критическую точку правосторонней критической области.

Если – нет оснований отвергнуть гипотезу о нормальном распределении генеральной совокупности. Другими словами, эмпирические и теоретические частоты различаются незначимо. Если – гипотезу отвергают. Другими словами, эмпирические и теоретические частоты различаются значимо.

Схема поиска критической точки:

α –> γ = 1 – α (по таблице) –> –> = х^кр_пр

2. Методические рекомендации для выполнения четвертого задания

и решение задания нулевого варианта

Задание 5. Выдвинуть гипотезу о виде закона распределения и проверить ее с помощью критерия Пирсона.

Х	6	8	10	12	14	16	18
пк	4	19	35	76	42	20	5

Решение.

1. Введем гипотезу: Н_о: генеральная совокупность имеет нормальное распределение. Для проверки гипотезы будем использовать критерий Пирсона.

2. В качестве критерия рассмотрим

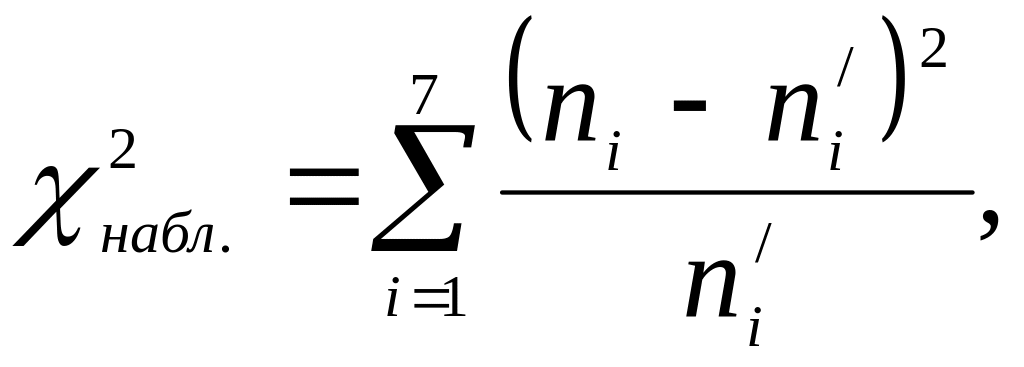где n_i – наблюдаемые частоты, n_i^/ – теоретические частоты; χ² – распределение имеет степени свободы: k = v – 3, т.е. k = 7 - 3 = 4.

3. Используя метод произведений, найдем выборочную среднюю и выборочное среднее квадратическое отклонение (см. задание 1): 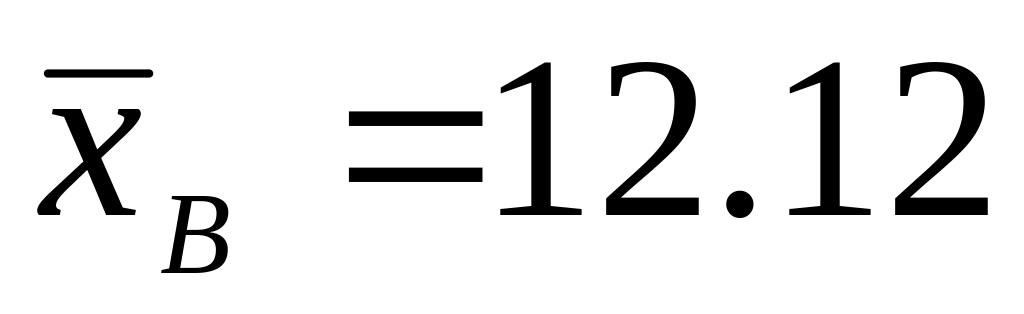, σ_В = 2.5.

4. Вычислим теоретические частоты, учитывая, что n = 201, h = 2, по формуле: .

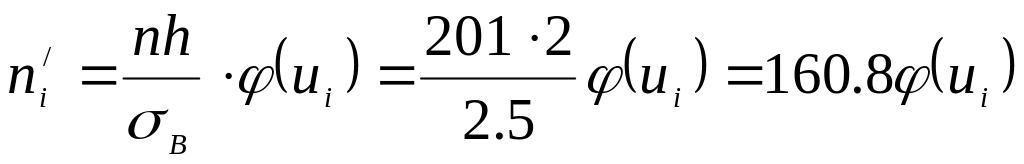5. Составим расчетную таблицу:

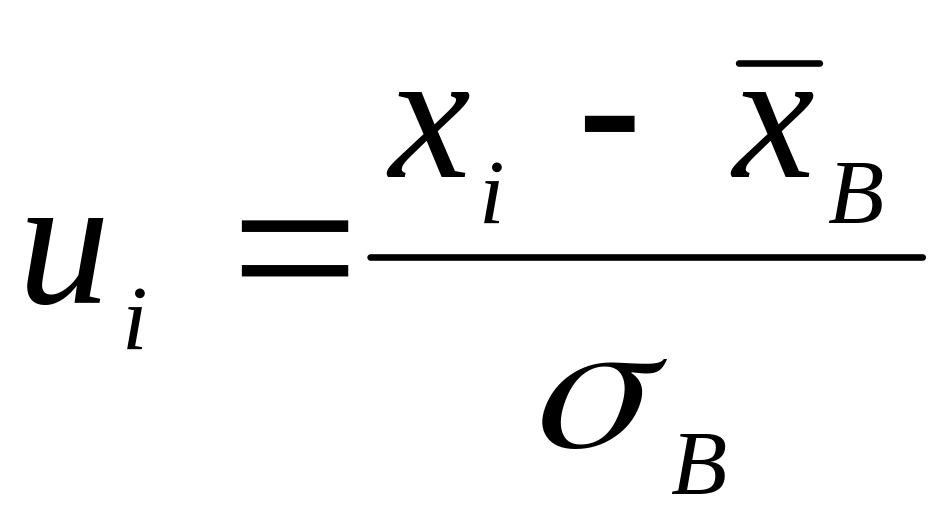
I	xi		φ(ui)	ni/ = 160.8φ(ui)
1	6	-2.45	0.0198	2.1146
2	8	-1.65	0.1023	10.9256
3	10	-0.85	0.2780	29.6904
4	12	-0.048	0.3984	42.5491
5	14	0.75	0.3011	32.1575
6	16	1.55	0.1200	12.816
7	18	2.35	0.0252	2.6914

6. Сравним эмпирические и теоретические частоты:

а) составим расчетную таблицу, из которой найдем наблюдаемое значение критерия

I	ni	ni/	ni – ni/	(ni – ni/)2	(ni – ni/)2/ ni/
1	4	2.11	1.89	3.57	1.69
2	19	10.93	8.07	65.12	5.96
3	35	29.69	5.31	28.2	0.95
4	76	42.55	33.45	1118.9	26.3
5	42	32.16	9.84	96.83	3.1
6	20	12.82	7.18	51.55	4.02
7	5	2.69	2.31	5.34	1.99
Σ	201	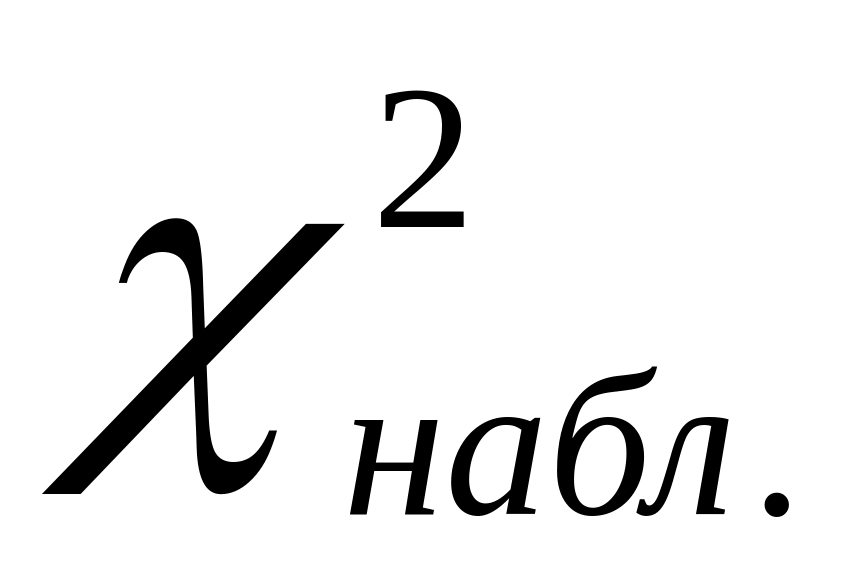			= 44.01

Из таблицы находим = 44.01;

б) по таблице критических точек распределения, по уровню значимости α = 0.05 и числу степеней свободы k = 4 находим критическую точку правосторонней критической области

Так как , то гипотезу о нормальном распределении генеральной совокупности отвергаем. Другими словами, эмпирические и теоретические частоты различаются значимо.