2.2. Основные теоретические вопросы и методические

рекомендации для выполнения второго задания

1. Понятие оценки. Генеральные совокупности характеризуются некоторыми постоянными числовыми характеристиками распределения. По выборкам можно найти оценки этих характеристик. Вследствие случайности выборок значения оценок одной числовой характеристики, вычисленные по разным выборкам из одной и той же генеральной совокупности, бывают, как правило, различными.

Обозначим неизвестный параметр распределения, т.е. числовую характеристику генеральной совокупности Х, через Θ, а оценку неизвестного параметра – через Θ^*. Оценка Θ^* – функция от вариант выборки. Оценки неизвестного параметра можно находить разными способами.

При оценивании возможны ошибки, поэтому к оценкам предъявляются определенные требования. Как было отмечено в пункте 2.1, оценки должны удовлетворять трем требованиям: быть несмещенными, эффективными и состоятельными.

Оценка Θ^* называется несмещенной для Θ, если математическое ожидание от нее равно оцениваемому параметру, т.е. М(Θ^*) = Θ. Если это условие не выполняется, то оценку называют смещенной, при этом смещение вычисляется как разность [М(Θ^*) – Θ].

Несмещенной оценкой среднего значения μ (математического ожидания) является среднее арифметическое (выборочное среднее). Выборочная дисперсия по отношению к генеральной дисперсии является смещенной оценкой. Поэтому для оценки генеральной дисперсии используется «исправленная» дисперсия = D_вn/(n-1).

Если сравнивать эту формулу с формулами для вычисления выборочной дисперсии, то можно получить аналогичные формулы для вычисления несмещенной оценки дисперсии:

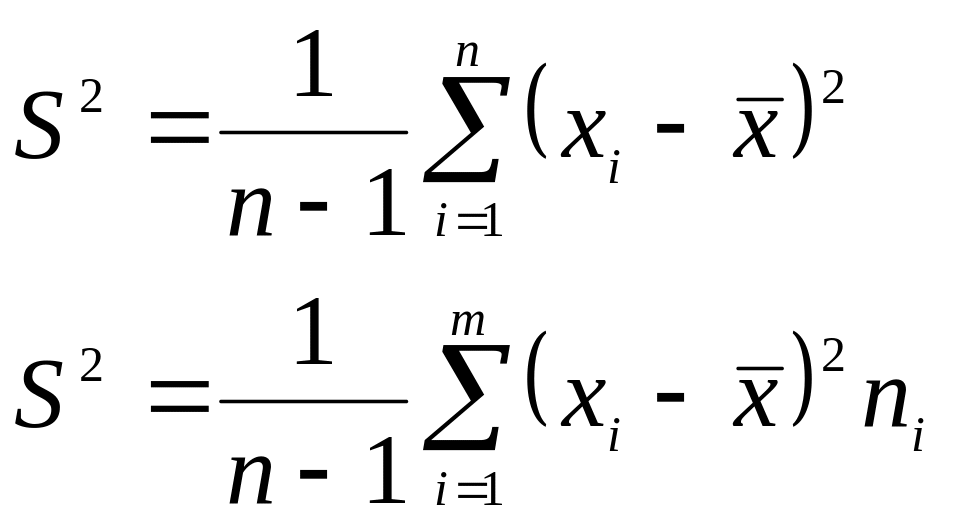
2. Доверительный интервал, доверительная вероятность. Оценку Θ^* неизвестного параметра Θ, рассмотренную выше, называют точечной, так как она определяет одно значение, одну точку на числовой оси. Все точечные оценки параметров распределения генеральной совокупности вычисляют по выборкам, но из-за случайности выборок оценки являются случайными величинами, отличающимися от постоянного значения параметра Θ. Обозначим точность оценки через Δ (Δ > 0), тогда |Θ - Θ^*| Δ. Чем меньше Δ, тем точнее оценка.

Однако любую точность оценки можно получить с определенной вероятностью, которая называется доверительной вероятностью γ, или надежностью: Р(|Θ - Θ^*| Δ) = γ.

Если преобразовать это выражение, то получим Р(Θ*- Δ Θ Θ^* + Δ) = γ.

Это означает, что интервал (Θ* - Δ , Θ^* + Δ) покрывает значение параметра Θ с заданной доверительной вероятностью γ. Точность оценки Δ фактически определяет длину интервала (2Δ). Доверительная вероятность γ задается обычно значением, близким к единице, например, 0.95, 0.99 и т.д.

Доверительная вероятность γ, точность оценки Δ и объем выборки n связаны между собой. Если определены две из этих величин, то тем самым будет определена и третья. Рассмотрим доверительные интервалы для некоторых числовых характеристик распределения признака Х генеральной совокупности.

3. Доверительный интервал для среднего значения а нормального распределения при известном σ. Пусть задана генеральная совокупность с нормальным распределением Х = N(а, σ), где значение стандартного отклонения σ известно. Для оценки параметра а воспользуемся величиной . Заметим, что и среднее арифметическое , и элементы выборки Х₁, Х₂, …, Х_n из-за случайности выборок являются случайными величинами. Все элементы выборки имеют то же распределение, что и генеральная совокупность: Х_i = N(а, σ), i =

1, 2, …, n. Легко показать, что среднее арифметическое также имеет нормальное распределение: = N(а, σ /√n). Получим

Р(| - а| Δ) = γ

С другой стороны, исходя из известной формулы теории вероятностей

(|Х - а| < є) = 2Ф(є/σ) для нормально распределенной случайной величины, заменяя Х на , получим:

Р(| - а| < Δ) = 2Ф(Δ√n/σ) = 2Ф(t), где t = Δ√n/σ. Откуда получаем:

t σ = Δ√n, или Δ = tσ/√n.

Рассмотренное выше позволяет утверждать, что

, где вместо t взято u_r , т.е. с надежностью γ доверительный интервал покрывает неизвестный параметр а при заданном σ.

Для поиска доверительного интервала находят значение переменной t = u_γ по таблице.

4. Доверительный интервал для среднего значения а нормального распределения при неизвестном σ. Пусть задана генеральная совокупность с нормально распределенным признаком Х = N(а, σ), причем значение стандартного отклонения σ неизвестно. Так как σ неизвестно, то непосредственно воспользоваться нормальным распределением N(а, σ) нельзя. Однако известно, что случайная величина Т = ( - а) √n/S, где S – «исправленная» дисперсия – несмещенная оценка стандартного отклонения генеральной совокупности, n – объем выборки, имеет распределение Стьюдента (t — распределение) с числом степеней свободы (n - 1).

Для получения интервальной оценки выполним те же преобразования и получим доверительный интервал (х_в - t_γ s/ √n; х_в + t_γ s/ √n), покрывающий среднее генеральное с надежностью γ.

Величина t_γ определяется по таблицам распределения Стьюдента. По нижней части головки таблицы; на основании условия определяется t_γ, но в данном случае имеем противоположное неравенство, значит, нужно использовать условие . Число степеней свободы равно (n – 1):

, где доверительный интервал указан в скобках.

5. Доверительный интервал для генерального среднеквадратического отклонения нормально распределенного признака Х. Предположим, что генеральная совокупность имеет нормальное распределение Х = N(а, σ ). Тогда случайная величина имеет χ² – распределение (распределение Пирсона) с числом степеней свободы (n – 1). Случайная величина с χ² – распределением принимает только неотрицательные значения. По таблицам χ² – распределения можно найти х_α, удовлетворяющее следующему условию:

Р(χ² > х_α) = α., где α = 1 – γ.

По таблицам χ² – распределения всегда можно найти такие числа u₁ и u₂, которые удовлетворяли бы условию .

Доверительный интервал для среднеквадратического, с учетом рассмотренного выше, можно найти так:

s(1 - q) < σ < s(1 + q), где q = q(γ, n) – табулированная случайная величина.