3. Методические рекомендации для выполнения пятого задания

и решение задания нулевого варианта

Задание 5. По заданной таблице 1:

а) найти выборочный коэффициент корреляции и проверить его значимость при α = 0.05;

б) найти уравнение выборочной линии регрессии;

в) построить график линии регрессии и сопоставить ее с графиком линии, построенной с помощью средних;

Таблица 1

Y	X
	9	11	13	15	17
1	9	1
2	8	12	1
3		7	26	2
4			6	8
5			4	10	3
6				2	1

Решение.

а) Найдем выборочный коэффициент корреляции и проверим его значимость. Для этого составим сначала таблицу 2 по условным вариантам, приняв С₁ = 13, h₁ = 2, C₂ = 4, h₂ = 1.

Таблица 2

V	U
	-2	-1	0	1	2	nv
-3	9	1				10
-2	8	12	1			21
-1		7	26	2		35
0			6	8		14
1			4	10	3	17
2				2	1	3
nu	17	20	37	22	4	n = 100

По таблице 2 найдем выборочные , ,σ_u, σ_v.

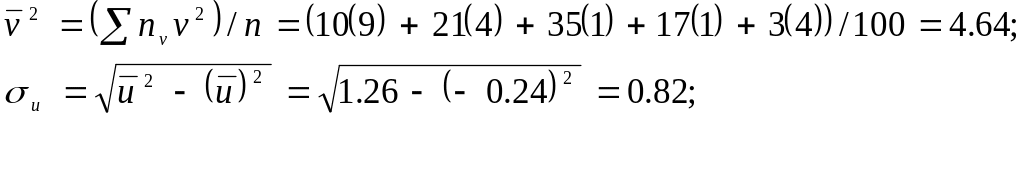
Cоставим таблицу 3.

Таблица 3

V	U
	-2	-1	0	1	2	ΣnuvU	vU
-3	-18 1 -27	-1 1 -3				-19	57
-2	-16 8 -16	-12 12 -24	0 1 -2			-28	56
-1		-7 7 -7	0 26 -26	2 2 -2		-5	5
0			0 6 0	8 8 0		8	0
1			0 4 4	10 10 10	6 3 3	16	16
2				2 2 4	2 1 2	4	8
V=ΣnuvU	-43	-34	-24	12	5		ΣvU=142
UV	86	34	0	12	10	ΣnV=142

По таблице 3 найдем выборочный коэффициент корреляции r_B.

Для проверки значимости выборочного коэффициента корреляции выдвинем гипотезу Н₀: r_г = 0 и подберем критерий для ее проверки ;

Проверим гипотезу по этапам:

Этап 1. Нулевая гипотеза Н₀: r_г = 0, конкурирующая Н₀: r_г ≠ 0.

Этап 2. Зададимся уровнем значимости α = 0.05 (задан по условию).

Этап 3. Воспользуемся критерием и найдем его численное значение при n = 100 и r_B = 0.75;

Этап 4. Найдем критическую область, которая является двусторонней, для чего воспользуемся таблицей и найдем t_кр. = 1.98. Таким образом, критической областью является совокупность двух областей (- ∞; - 1.98) и (1.98; ∞).

Этап 5. Так как численное значение критерия принадлежит критической области, то выборочный коэффициент корреляции значим, что подтверждает факт корреляционной зависимости между Х и Y.

б) Найдем уравнение выборочной линии регрессии Y на Х в виде , для чего воспользуемся формулами:

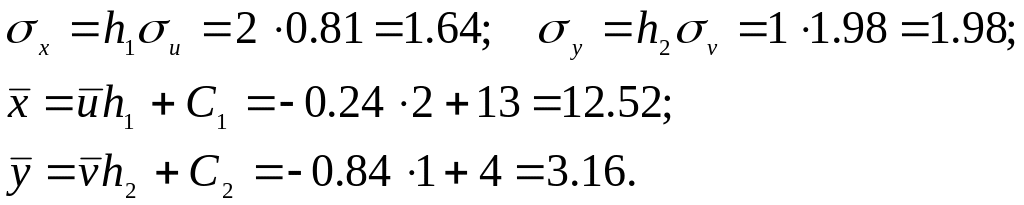
Подставим найденные значения в искомое уравнение регрессии, получим: или .

в) Построим график линии регрессии и сопоставим ее с графиком линии, построенной с помощью средних, т.е. проверим согласованность, сравнивая средние, вычисленные: а) по условию; б) по корреляционной таблице.

x₁ = 9

х₂ = 11

х₃ = 13

х₄ = 15

х₅ = 17

Для сравнения составим таблицу 4.

Таблица 4

По уравн.	-0,04	1,78	3,6	5,42	7,24
По таблице	1,47	2,3	3,35	4,55	5,25

Изобразим данные на графике.