49

Глава 2. Методические рекомендации к выполнению

домашней контрольной работы

2.1. Основные теоретические вопросы и методические

рекомендации для выполнения первого задания

1. Генеральная и выборочная совокупности. Совокупность – это множество объектов (единиц совокупности), обладающих массовостью, однородностью, определенной целостностью, взаимозависимостью состояния отдельных единиц и наличием вариации. Единицы статистической совокупности характеризуются общим свойством, которое в статистике получило название признака. В статистике рассматриваются совокупности генеральные и выборочные. Генеральная совокупность – совокупность объектов, из которой выбираются единицы и исследуются на наличие определенного признака. Выборочная совокупность – случайно отобранные объекты из генеральной совокупности.

Достаточно часто полное исследование генеральной совокупности практически невозможно или неэкономично, требует больших материальных затрат. Поэтому всеобщее исследование применяют, как правило, редко.

Обычно из генеральной совокупности делают выборку и осуществляют исследование ее объектов. С помощью выборки оценивают генеральную совокупность по вероятностным свойствам. Чтобы оценки были достоверными, выборка должна быть представительной, т.е. ее вероятностные свойства должны совпадать или быть близкими к свойствам генеральной совокупности.

Представительную выборку можно получить, если выбирать объекты для исследования случайно, т.е. гарантировать всем объектам генеральной совокупности одинаковую вероятность подвергнуться исследованию.

При исследовании объектов можно фиксировать или измерять значение одного или нескольких признаков. Соответственно говорят об одномерной, двумерной, трехмерной и т.д. выборках. Рассмотрим обработку одномерных выборок.

2. Статистическое распределение выборки. Будем обозначать значения признака Х генеральной совокупности через х_i и называть вариантами. Пусть из генеральной совокупности извлечена выборка, причем х₁ наблюдалось n₁ раз, x₂ – n₂ раза, x_k – n_k раз, где Σn_i = n – объем выборки. Наблюдаемые значения x_i располагают в виде последовательности, записанной в возрастающем порядке, и называют ее вариационным рядом. Числа наблюдений n_i называют частотами, а их отношения к объему выборки – n_i/n = w_i – относительными частотами.

Статистическим распределением выборки называют перечень вариант и соответствующих им частот (статистическое распределение частот или статистический ряд частот) или относительных частот (статистическое распределение частот или статистический ряд частот). Статистическое распределение выборки (статистический ряд) можно задать также в виде последовательности интервалов и соответствующих им частот (в качестве частоты, соответствующей интервалу, принимают сумму частот, попавших в этот интервал вариант).

Статистический ряд оформляют в виде таблицы:

хi	Х1	х2	…	хk
ni	n1	n2	…	nk

3. Эмпирическая функция распределения. Каждая генеральная совокупность имеет функцию распределения F(x) (ее называют теоретической функцией распределения), которая обычно неизвестна. По выборке можно найти функцию распределения F^*(x), которую называют эмпирической функцией распределения. Эмпирическая функция распределения для дискретного признака Х находится аналогично как в теории вероятностей, она находится для случайной величины, где вместо вероятностей p_i берутся относительные частоты n_i/n, т.е.

,

.

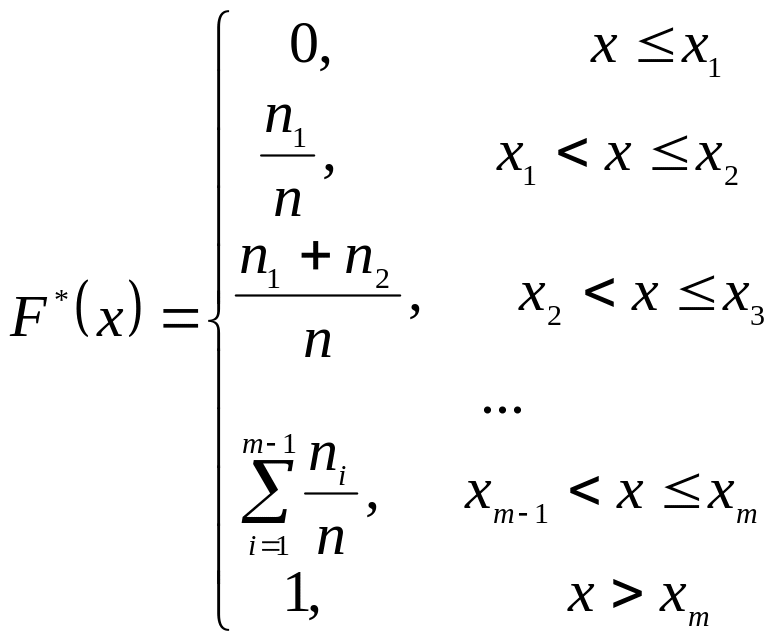Значениями эмпирической функции распределения являются так называемые накопленные частоты. График эмпирической функции распределения строят так же, как и график функции распределения F(x) дискретной случайной величины.

4. Полигон и гистограмма. Для наглядности строят различные графики статистического распределения признака Х, в частности, полигон и гистограмму. Рассмотрим построение полигона и гистограммы для точечного и интервального задания статистического ряда.

A. Дискретное распределение выборки. Для построения полигона частот на оси абсцисс откладывают варианты x_i, а на оси ординат – соответствующие им частоты n_i. Полученные точки (x_i; n_i) соединяют отрезками и получают ломаную, которая и называется полигоном частот.

Полигоном относительных частот называют ломаную, отрезки которой соединяют точки (x₁; w₁), (x₂; w₂),…, (x_k; w_k). Для построения полигона относительных частот на оси абсцисс откладывают варианты x_i, а на оси ординат – соответствующие им относительные частоты w_i.

Б. Непрерывное распределение признака. При непрерывном распределении признака целесообразно строить гистограмму частот и относительных частот.

Гистограммой частот называют ступенчатую фигуру, состоящую из прямоугольников, основаниями которых служат заданные интервалы, длины h, а высоты равны отношению n_i/h (плотность частоты).

Для построения гистограммы частот на оси абсцисс откладывают интервалы, а над ними проводят отрезки, параллельные оси абсцисс на расстоянии n_i/h.

Площадь частичного прямоугольника равна hn_i/h = n_i – частоте вариант интервала; следовательно, площадь гистограммы частот равна сумме всех частот, т.е. объему выборки.

Гистограммой относительных частот называют ступенчатую фигуру, состоящую из прямоугольников, основаниями которых служат частичные интервалы длины h, а их высоты равны отношению w_i/h (плотность относительной частоты).

Для построения гистограммы относительных частот на оси абсцисс откладывают частичные интервалы, а над ними проводят отрезки, параллельные оси абсцисс на расстоянии w_i/h. Площадь частичного прямоугольника равна hw_i/h = w_i – относительной частоте вариант, попавших в этот интервал. Следовательно, площадь гистограммы относительных частот равна сумме всех относительных частот, т.е. единице.

5. Генеральная и выборочная средние. Пусть исследуется генеральная совокупность на количественный признак Х, принимающий значения х_{1 ,} х₂ ,…, х_к. Средним арифметическим генеральной совокупности называется _г = ∑(N_i х_i)/N, где х_i – значения признака, а N_i – частоты (или весы), N = ∑N_i – объем генеральной совокупности. Если составлен статистический ряд, то средним выборочным называется _в = ∑(n_i х_i)/n, где х_i –варианты, а n_i – соответствующие частоты (или весы), n = ∑n_i – объем выборочной совокупности.

6. Генеральная и выборочная дисперсии. Пусть исследуется генеральная совокупность на количественный признак Х. Осуществлена выборка. Разности (х_i - _г) и (х_i - _в) называют отклонениями средних от значений признака. Генеральной дисперсией называется число, равное среднему арифметическому квадратов отклонений значений признака Х от генеральной средней, т.е. D_г = ∑N_i (х_i - _г)² /N.

Выборочной дисперсией называется число, равное среднему арифметическому квадратов отклонений вариант от средней выборочной, т.е.

D_в = ∑n_i (х_i - _в)² /n.

При решении статистических задач часто вместо дисперсии используют среднеквадратическое отклонение, которое обозначается σ_г² = D_г и σ_в² = D_в.

7. Статистические оценки параметров распределения. Пусть исследуется генеральная совокупность на некоторый признак Х. И пусть по некоторому теоретическому соображению удалось установить закон его распределения. Так как генеральную совокупность часто исследователь нельзя, то осуществляют выборку, находят ее числовые характеристики и по ним оценивают параметры генеральной совокупности. Оценить означает, приближено заменить. При этом могут быть допущены ошибки. Поэтому для осуществления оценки к ней предъявляются требования: несмещенности, эффективности и состоятельности. В науке статистике установлено, что средняя выборочная удовлетворяет таким требованием и служит для оценки генеральной средней. Для выборочной дисперсии такие требования не выполняются. Поэтому оценивают генеральную дисперсию с помощью «исправленной выборочной» .

= ∑n_i (х_i - )² /(n - 1). Стандартное или среднеквадратичное отклонение определяется как квадратный корень из дисперсии .

8. Метод произведений для вычисления выборочной средней и дисперсии. Метод произведений дает удобный способ вычисления условных моментов различных порядков статистического ряда. Введем понятие равноотстоящих вариант. Варианты называют равноотстоящими, если «расстояния» между соседними вариантами одинаковые. Пусть выборка задана в виде распределения равноотстоящих вариант и соответствующих им частот. В этом случае удобно находить выборочную среднюю и дисперсию методом произведений по формулам

_в = М₁^*h + C, D_в = [М₂^* - (М₁^*)²]h² , где h – шаг (разность между двумя соседними вариантами); С – ложный нуль (варианта, которая расположена примерно в середине вариационного ряда); М₁^* = ∑n_i u_i /n – условный эмпирический момент первого порядка, М₂^* = ∑n_i u_i² /n – условный эмпирический момент второго порядка, u_i = (x_i - C)/h – условная варианта.

Если первоначальные варианты не являются равноотстоящими, то интервал, в котором заключены все варианты выборки, делят на несколько равных, длины h, частичных интервалов (каждый частичный интервал должен содержать не менее 8-10 вариант). Затем находят середины частичных интервалов, которые и образуют последовательность равноотстоящих вариант. В качестве частоты каждой середины интервала принимают сумму частот вариант, которые попали в соответствующий частичный интервал.

9. Метод сумм для вычисления выборочной средней, дисперсии, эксцесса и асимметрии. Пусть выборка задана в виде распределения равноотстоящих вариант и соответствующих им частот. Пусть требуется оценить параметры признака Х, нормального распределенного. Это можно сделать либо с помощью метода произведений, либо с помощью метода сумм. Изложим метод сумм. Метод сумм состоит в том, что условные моменты находят по формулам:

М₁^* = d₁ /n, М₂^* = (s₁ + 2s₂)/n, М₃^* = (d₁ + 6d₂ + 6d₃)/n, М₄^* = (s₁ + 14s₂ + 36s₃ + 24s₄)/n, где d_k = a_k – b_k, s_k = a_k + b_k. Тогда выборочные параметры можно найти так: _в = М₁^*h + C, D_в = [М₂^* - (М₁^*)²]h² , А_s = m₃ /σ_в³, Е_к = m₄ /σ_в⁴ - 3, где центральные эмпирические моменты 3-го и 4-го порядков вычисляются:

m₃ = [М₃^* - 3М₁^* М₂^* + 2(М₁^* )³]h³,

m₄ = [М₄^* - 4М₁^* М₃^* + 6(М₁^*)² М₂^* - 3(М₁^*)⁴]h⁴.