Кинематика материальной точки

• С редняя и мгновенная скорости материальной точки

[v] = 1 м/с.

где - элементарное перемещение точки за промежуток времени t; - радиус-вектор точки, s - путь, пройденный точкой за промежуток времени t. [r] = 1 м, [s] = 1 м,

• Среднее и мгновенное ускорение материальной точки [a] = 1 м/с².

• П олное ускорение при криволинейном движении - где - тангенциальная составляющая ускорения, - нормальная составляющая ускорения (R - радиус кривизны траектории в данной точке).

• Путь и скорость для равнопеременного движения

где - начальная скорость.

• Угловая скорость - [] = 1 рад/с. [] = 1 с^-1.

• Угловое ускорение - [] = 1 рад/с². [] = 1 с^-2.

Угловая скорость для равномерного вращательного движения точки по окружности - где Т - период вращения, n - частота вращения, (n = N/t , где N - число оборотов, совершаемых телом за время t).

• Угол поворота и угловая скорость для равнопеременного вращательного движения

где ₀ - начальная угловая скорость. Угол поворота , где N - число оборотов, совершаемых телом за время t.

• Связь между линейными и угловыми величинами:

s = R, v =R, a_= R, a_n =²R, где R - расстояние от оси вращения.

Динамика поступательного и вращательного движения

Динамика материальной точки

• Импульс (количество движения материальной точки)

• Второй закон Ньютона (основное уравнение динамики материальной точки)

где - сила, = 1Н, - импульс силы, = 1Нс.

Это же уравнение в проекциях на касательную и нормаль к траектории точки

М еханика твердого тела.

• Момент инерции материальной точки

где m -масса точки, r - расстояние до оси вращения. [I] = 1кгм².

• Момент инерции системы (тела)

где r_i - расстояние материальной точки массой m_i до оси вращения. В случае непрерывного распределения масс

• Моменты инерции тел правильной геометрической формы (тела считаются однородными, m -масса тела).

Т ело	П оложение оси вращения	Момент инерции
Полый тонкостенный цилиндр (кольцо), радиусом R	О сь симметрии	mR2
Сплошной цилиндр или диск радиусом R	Ось симметрии	(1/2)mR2
Прямой тонкий стержень длиной l	О сь перпендикулярна стержню и проходит через его середину	(1/12)ml2
П рямой тонкий стержень длиной l	Ось перпендикулярна стержню и проходит через его конец	(1/3)ml2
Ш ар радиусом R	Ось проходит через центр шара	(2/5)mR2

• Теорема Штейнера I = I_C + md²,

где I_C (I₀) - момент инерции относительно оси, проходящей через центр масс; I - момент инерции относительно параллельной оси, отстоящей от первой на расстоянии d; m - масса тела.

• Момент силы относительно неподвижной точки

где радиус-вектор, проведенный из этой точки в точку приложения силы . Модуль момента силы

где l плечо силы (кратчайшее расстояние между линией действия силы и осью вращения), [M] = 1 Нм.

• Момент импульса (момент количества движения) твердого тела относительно оси вращения

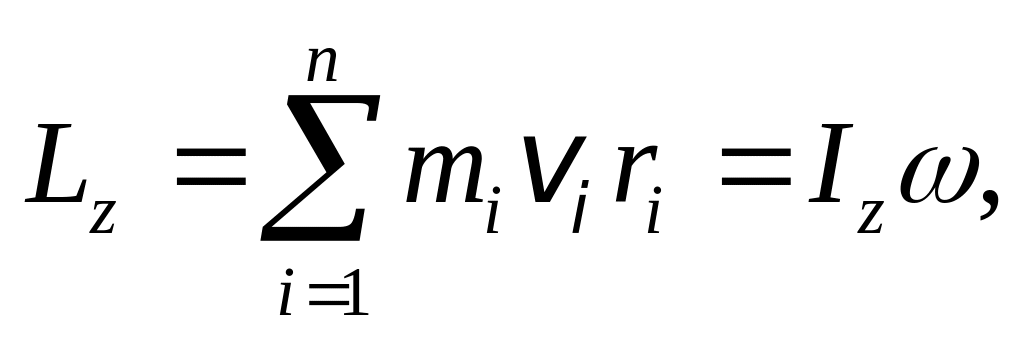
где r_i- расстояние от оси z до отдельной частицы тела; m_iv_i - импульс этой частицы; I_z - момент инерции тела относительно оси z;  - его угловая скорость. [L] = 1 кгм²с^-1.

• Уравнение (закон) динамики вращательного движения твердого тела относительно неподвижной оси

где  - угловое ускорение, I_z - момент инерции тела относительно оси z.