Значення робіт

№полож.	1	2		12

4. У тих самих координатах (під графіком M_п(), при збігу напрямків осі ординат) із масштабними коефіцієнтами _А і _ будують залежності А_с() і А_д()

(3.45)

5. Обчисляють постійний момент рушійних сил М_д

(3.46 )

і в координатах кривої M_п() будують у масштабі _М пряму M_д() паралельно осі абсцис.

6. Будують під графіками А_с() і А_д() у масштабах _А і _ графік зміни кінематичної енергії Е(). Вісь ординат “Е” цього графіка служить продовженням осі ординат “А” графіків робіт і по цій осі для відповідних кутів повороту _і вхідної ланки відкладають різницю ординат залежностей А_д() і А_с().

Таким чином, графіки моментів M_д() і M_н(), робіт А_д() і А_с() і зміни енергії Е() розташовуються друг під другом.

7. Будують в обраних масштабах _j і _ графік приведеного моменту інерції J_n(), користуючись даними табл. 3.2. При цьому вісь абсцис  розташовують вертикально, а вісь ординат J - горизонтально, як продовження осі абсцис графіків моментів.

8. Виключаючи графічно кут , будують діаграму Е - J_n. Для цього через ординати, що відповідають однієй і тій же абсцисі на кривих Е() і J_n(), проводять горизонтальну (для ординат кривої Е()) і вертикальну (для ординат кривої J_n()) лінії. Точка перетинання цих ліній визначить одну точку «петлі Вітенбауера» Е(J_n). Визначив усі 12 точок «петлі», з'єднують їх за допомогою лекала плавною кривою, одержуючи в масштабах _А і _J залежність, на якій горизонтальна вісь абсцис визначає розмір J_n, а вісь ординат - Е.

9. Під кутами _max і _min до осі J_n до зовнішніх точок петлі проводять дотичні AB і CD.

(3.47)

10. Ці дотичні відтиняють на осі E відрізок BD, що відбиває в масштабі _A найбільша зміна кінетичної енергії маховика протягом періоду сталого прямування машин.

Визначають момент інерції маховика по формулі:

(3.48)

На приведеному в додатку малюнку показаний приклад побудови діаграми Виттенбауэра.

На листі, де накреслені графіки і петля Виттенбауэра, необхідно в масштабі вичертит маховик, параметри якого визначають відповідно до залежностей «3.38» і «3.39».

4. Синтез кулачкового механізму

Студент вирішує задачу синтезу кулачкового механізму, представивши розрахунок пояснительной записки, а графічну частину - на четвертому листі.

Кулачковые механізми служать для забезпечення необхідного закону прямування вихідної ланки силових механічних системах і системах керування машин і механізмів. Основні розміри кулачка в проекті визначають з умови обмеження рогу тиску, що виключає самогальмування механізму.

4.1. Вихідні дані для синтезу плоского кулачкового механізму

Схеми кулачкових механізмів

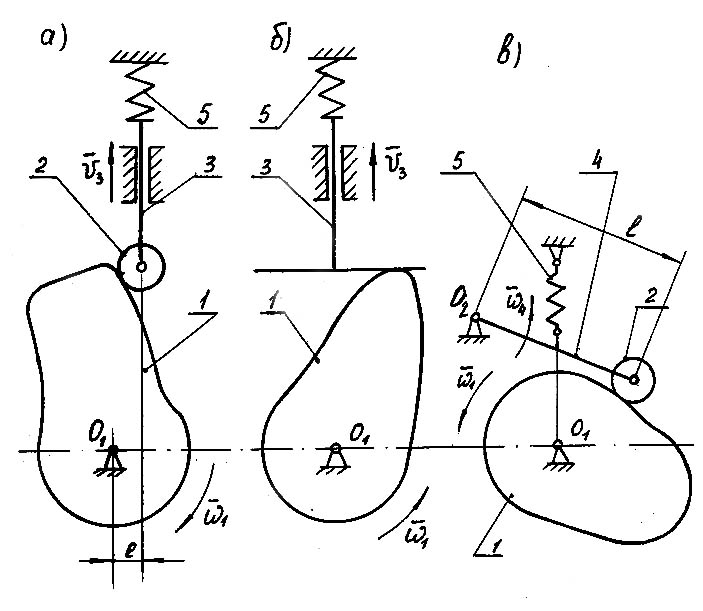
Мал.4.1

а), б) – з возвратно-поступальими рухомим товкачем;

в) – з хитним коромислом

1. кулачок; 2 – ролик; 3 – товкач; 4 – коромисло; 5 – пружина;

е – ексцентриситет; l – довжина коромисла.

У завданні на курсовий проект приведені такі, необхідні для синтезу кулачкового механізму, вихідні дані:

- схема кулачкового механізму /мал.4.1./ із движущет зворотно-поступально штовхачем (мал.4.1. а, б) або з коромислом, що чинить качательные прямування, (важелем) (мал.4.1. в);

- зсув “e” для штовхача, що поступально рухається, щодо центру обертання кулачка (мал.4.1. а);

- закон прямування кулачка (_K =const);

- максимальне лінійне переміщення S_max штовхача (S_max=h ) або кутове переміщення (_max) коромислом;

- закон зміни аналога прискорення штовхача (d²S/d²) або коромисла (d²/d² ), де - ріг повороту кулачка;

- фазові роги повороту кулачка:

• _n- підйому або _y- видалення штовхача (коромисла);

• _o - опускання або _c зближення штовхача (коромисла);

• _вв - верхнього вистою або _д- дальнього стояння штовхача (коромисла);

що-припускається ріг тиску _доп ;

- довжина l коромисло підоймового кулачкового механізму.

Для пояснення вихідних даних на мал.4.2.а показана сполучена схема кулачкового механізму зі штовхачем, що поступально рухається, і коромислом 2, на якій позначені фазові роги повороту ключа, що визначають ріг _p робочого профілю:

_p =_n+_o+_вв (4.1 )

поточний ріг тиску _і між нормаллю n-n в точці профілю кулачка й абсолютної швидкості точки контакту вихідної ланки; ріг _нв нижнього вистою ( _ - ближнього стояння; початковий радіус кулачка R_o; теоретичний початковий радіус кулачка r_o початковий радіус центрового профілю, що є траєкторії осі ролика у відносному його коченні по конструктивному профілі кулачка); початок відліку “o” переміщення S штовхача 2 і рогу повороту коромисла 2; поточне значення _і рогу повороту кулачка.

На рис 4.2б без масштабу приведений графік переміщення S штовхача (рогу повороту  коромисла) у функції рогу повороту  кулачка за цикл (_ц=2П ). Цю криву одержують із вихідних даних шляхом двухкратного графічного інтегрування залежності аналога прискорення, що буде розглянуто нижче (п.4.3).

4.2. Формулювання задачі проектування кулачкового механізму

Задачею синтезу кулачкового механізму є побудова профілю кулачка, виходячи з кінематичних, динамічних, конструктивних і технологічних вимог, запропонованих до машини. При рішенні цієї задачі послідовно здійснюють динамічний і кінематичний синтез кулачка

Задача динамічного синтезу кулачка - визначення мінімального радіуса профілю кулачка, при якому перемінний ріг тиску _і в жодному положенні кулачкового механізму не буде перевищувати припустиме значення _доп. У противному випадку, як відомо, відбудеться заклинювання кулачкового механізму.

При синтезі коромислового кулачкового механізму додатково вирішують задачу визначення відстані між центрами кулачка і коромисла О₁О₃ заданої довжини коромисла. Задача кінематичного синтезу кулачкового механізму полягає у визначенні (по заданим вихідним даним і на підставі результатів динамічного синтезу кулачкового механізму) теоретичного і дійсного профілів кулачка.

Сполучений кулачковий механізм.

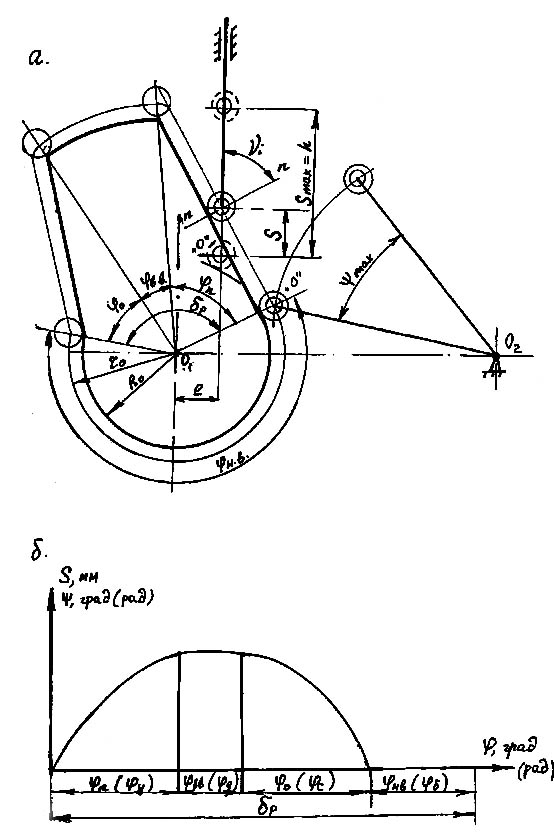
Мал. 4.2

а – кінематична схема; б – графік переміщення товкача (кут повороту коромисла)

При цьому проектування профілю кулачка здійснюють загальними прийомами побудови взаимоогибает кривых.

У методичних указівках розглядаються принципи рішення задач синтезу кулачкового механізму для кінематичних схем, поданих на мал. 4.1 а і мал. 4.1 в.

4.3 Графічне інтегрування кінематичних діаграм

Для синтезу кулачкового механізму в якості вихідних даних повинна бути задана залежність S() лінійного переміщення штовхача (для штовхача, що зворотно-поступально рухається,) або залежність () кутового переміщення коромисла (для хитного прямування вихідного елемента). Як указувалося вище (п.4.1), для одержання цієї залежності необхідно двічі проинтегрировать вихідну функцію аналога прискорення d²S/d²(d²/d²) . Роздивимося принцип графічного інтегрування на прикладі інтегрування довільної функції d²у/dx²(у^) , зображеної на мал. 4.3. Для цього:

- вісь абсцис у межах існування функції розбивають на деяке «К» число відрізків із рівним або нерівним кроком X , на яких роблять кусочно-лінійну апроксимацію вихідної функції (мал. 4.3);

- на кожному кроку виконують осреднение аппроксимированной функції за принципом рівності площі криволінійної трапеції і прямокутника, тобто визначають середини інтервалів “в”, “с”…;

- середнє значення ординати на кожному кроку (мал.4.3 а) (ab - на кроку ; O₁-1, cd - на кроку 1-1^ і т.д.) проектують на вісь ординат о₁в^ =ав, о₁d^ і т.д.);

- з'єднують довільно узяту точку (полюс) на продовженні осі з точками ;

- під графіком первообразной «у» проводять осі координат для що інтегрується функції «у» із початком координат O₂ (мал.4.3 б);

- із точки O₂ ( мал.4.3 б) проводять відрізок O₂в в інтервалі паралельно променю H₁d^, відрізок вd в інтервалі 1-1^ паралельно променю P₁d^і т.д.

Отримана ломаная крива ( у межі, при X0 - крива) у графічному виді являє собою з урахуванням масштабів, про які буде сказано нижче, інтеграл заданої залежності У/Х/ (тобто криву У^/Х/ ).

Аналогічно, інтегруючи криву у^/х/, одержуемо шукану інтегральну криву у/х/ . На графіку кривой у^/х/ у якості полюса на осі Х (мал. 4.3. б) прийнята довільна точка (P₂(O₂P₂=H₂ ).

Для визначення довільних постійних інтегрування задають початкові умови: при X = 0; У^= 0; У= 0.