3.5.Обчислення приведеного до вхідної ланки моменту інерції.

Як відомо [2,3], приведення моментів інерції окремих ланок механізму до ланки приведення припускає рівність кінетичної енергії i-тих ланок у заданому положенні й умовної кінетичної енергії, якою володіє ланка приведення в тому ж положенні і для ланки приведення, що рухається обертально, ця рівність має вигляд

(3.32)

де n - число ланок механізму; J_n - приведений (до ланки приведення) момент інерції; _пр - кутова швидкість ланки приведення.

У випадку плоскопаралельного руху і-тої ланки її кінетична енергія визначається:

,(3.33)

де m - маса i-тої ланки; V_Si - швидкість центру мас i-тої ланки (визначають із плану швидкостей); J_Si - момент інерції i-тої ланки щодо центральної осі, перпендикулярної площини руху (для однорідної ланки, виконаного у виді стержня довжиною ; _i- кутова швидкість i-тої ланки (визначають при кінематичному аналізі механізму).

З формули (3.32) визначають J_n, підставивши в її ліву частину вираз для E_i (3.33)

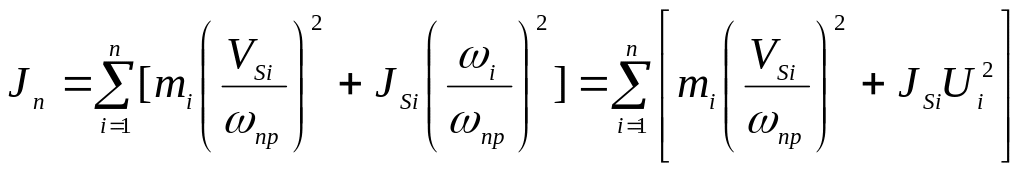(3.34)

де U_i - передатне відношення між i-тою ланкою і ланкою приведення. У формулі (3.34) враховується момент інерції приводного двигуна

(3.35)

де U_p - передатне число редуктора.

Результати розрахунку приведеного моменту інерції механізму для 12-ти положень механізму зводять у табл.3.2.

Таблиця 3.2

Значення приведеного моменту інерції

№ полож.	1	…		…	12
Jn

Виписуючи значення J_n з табл. 3.2, за допомогою попередньо обраних масштабних коефіцієнтів моменту інерції _J і кута повороту _ , будують графічну залежність J_n(), для чого обчисляють зображення приведеного моменту інерції

(3.36)

По осі абсцис відкладають, як і при побудові графіка M_np() 12 відрізків , а по осі ординат, паралельно їй для кожної точки - відповідні положення кривошипа значення .

3.6. Визначення розмірів маховика

Маховик установлюють на валі кривошипа, і він служить для забезпечення необхідної рівномірності ходу підоймового механізму. При заданих силах і середній кутовій швидкості ₁ вхідної ланки коефіцієнт нерівномірності ходу машини обчисляють по формулі 1,2

(3.37)

який залежить від постійної складового приведеного моменту інерції машини. Чим більше ця складова, тим менше коефіцієнт . Практикою встановлені значення коефіцієнта  для різноманітних типів машин. Розрахований раніше (п.3.5) приведений момент J_n інерції для всіх положень часто надається недостатнім для забезпечення заданого значення коефіцієнта . У цьому випадку на вхідному валі додатково встановлюють маховик із таким моментом інерції J_M, при якому заданий коефіцієнт  забезпечується.

Маховик, як правило, виконують у виді колеса з масивним обідом, що з'єднується зі ступицей спицями. Зневажаючи по розуміннях інерційності масою спиць і ступици маховика і знаючи його момент інерції J_M, можна визначити геометричні розміри маховика. Так, задаючи габаритний (зовнішній) діаметр D маховика і його товщину  визначають ширину маховика:

(3.38)

де  - щільність матеріалу маховика (для сталі  = 7800 кг/м).

З урахуванням маси спиць і ступиці маховика його повну масу визначають із вираження

(3.39)

Таким чином, для визначення геометричних розмірів маховика і його маси необхідно визначити момент інерції маховика, виходячи з заданого за умовою курсового проекту коефіцієнта нерівномірності ходу машини. Для цього існує декілька засобів. При виконанні курсового проекту застосовують засіб Ф.Вітенбауера, відповідно до яких будують «петлю Вітенбауера», що подає графічну залежність між збільшенням кінетичної енергії і кутом повороту кривошипа:

(3.40)

(3.41)

Е - зміна кінематичної енергії, що відповідає куту повороту  вхідної ланки щодо його початкового положення;

А_д - робота рушійних сил на куті повороту вхідної ланки:

(3.42)

М_д - момент рушійних сил, що відповідає кутові повороту вхідної ланки;

А_с - робота сил корисного опору

(3.43)

М_п -момент сил корисного опору, що відповідає рогові повороту вхідної ланки.

Порядок побудови «петлі Вітенбауера» такий:

1. Будують у заздалегідь обраних чисельних значеннях масштабів _м і _ криву М_пр() (п.3.4.).

2. Визначити роботу сил опору А_с для кожного кута повороту _i вхідної ланки

(3.44 )

де - масштабний коефіцієнт роботи; S - площа фігури на графіку M_пр(), обмежена віссю абсцис, кривої моментів сил опору і вертикальної лінії, проведеної через абсцису _і кінця відповідної ділянки кривої. Причому, площі визначають із знаками (своїми), і результати розрахунку по всім 12-ти кутам повороту вхідної ланки заносять у табл 3.3

3.У табл.3.3 уписують також значення роботи рушійних сил.

При цьому враховують, що залежність А_д() - пряма лінія (М_д=const), що проходить через початок координат. Ординати цієї прямой визначають з умови, що за цикл робота рушійних сил дорівнює роботі сил опору, тобто за цикл А_д=А_с.

Таблиця 3.3