2. Расчетная часть

2.1 Составление системы уравнений по законам Кирхгофа

и представление её в дифференциальной и символической

формах

Система уравнений в дифференциальной форме:

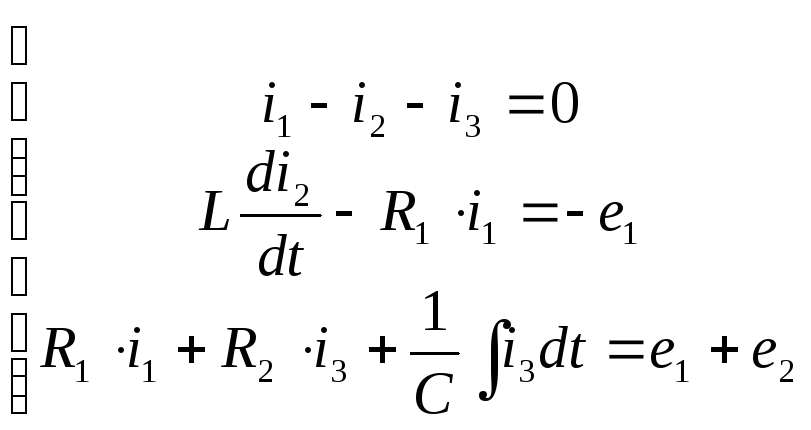
Система уравнений в символической форме:

2.2 Расчёт токов в ветвях

Для расчёта токов в ветвях воспользуемся методом междуузлового напряжения.

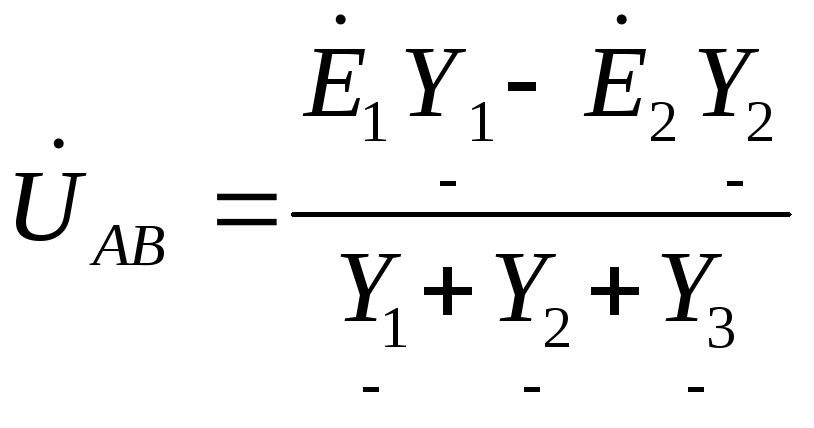
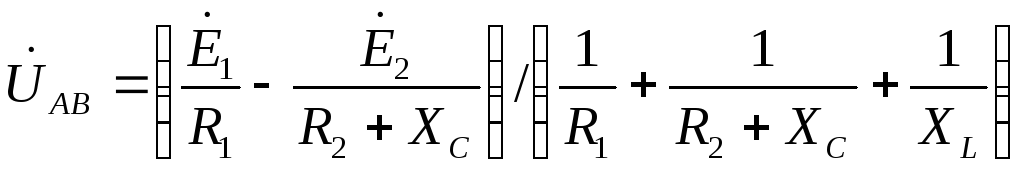
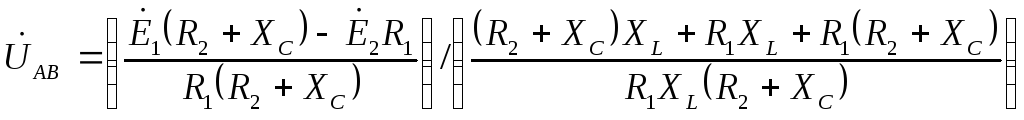
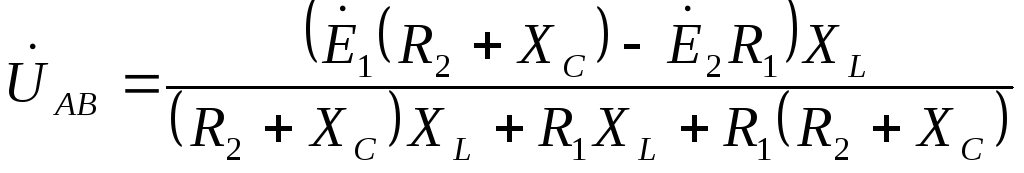
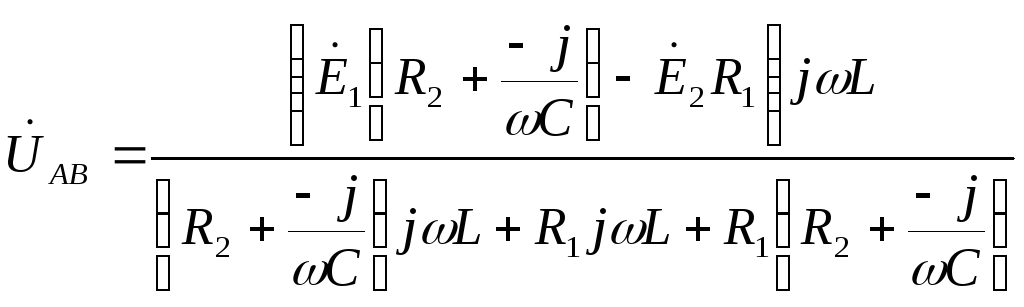
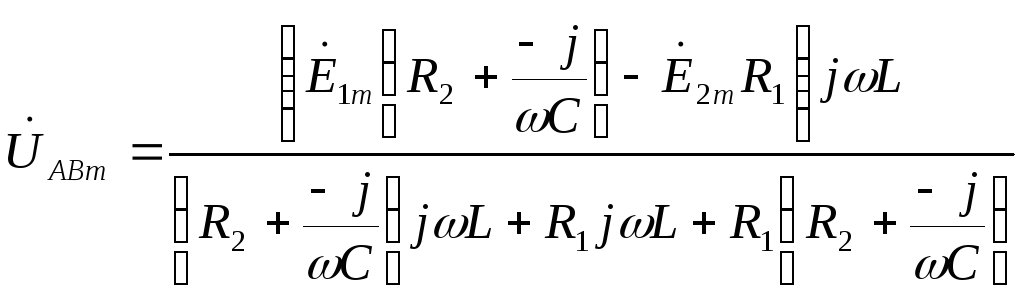
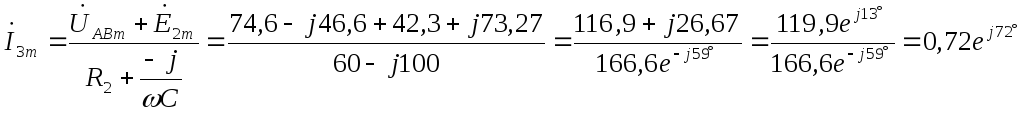
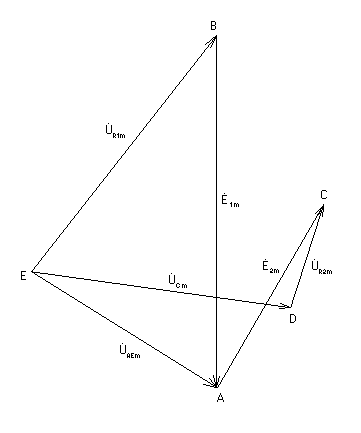
2.3 Расчёт потенциалов точек цепи

Представим данную схему в виде:

Представим , и в комплексном виде:

При построении диаграммы предположим, что .Для определения потенциалов остальных точек цепи обойдём контур цепи в направлении, противоположном положительному направлению тока или, как принято говорить, против тока. При таком обходе контура комплексный потенциал каждой последующей точки будет определяться как сумма комплексного потенциала предыдущей точки и комплексного напряжения на элементе, включённом между ними.

Для первой ветви можно записать:

Для второй ветви:

Для третьей:

4. Построение временных графиков мгновенных значений тока в

одной из ветвей и напряжения между узлами электрической цепи

Для наглядности приводятся графики указанных функций в двух масштабах по оси t.

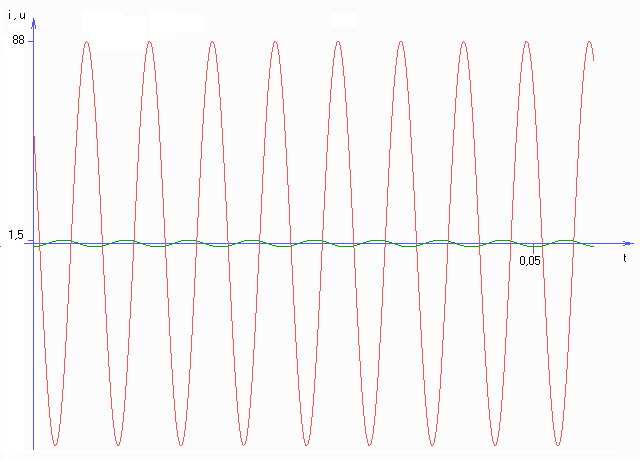
3. Вывод

В результате расчётов были получены токи в ветвях электрической цепи с несколькими источниками э.д.с. и с резистивными, емкостным и индуктивным приёмниками. Были определены потенциалы точек электрической цепи и построена топографическая диаграмма, с помощью которой можно найти напряжения между двумя любыми точками цепи. Графически представлены мгновенные значения некоторых величин электрической цепи, что даёт представление о процессах происходящих в ней в определённый момент времени.

Используемая литература.

1. Бессонов Л.А. Теоретические основы электротехники.- М.:Высшая школа, 1978.

2. Зевеке Г.В. и др. Основы теории цепей.- М.: Энергия, 1975.

3. Электротехника п.р. проф. Герасимова В.Г. – М.: Высшая школа, 1985.

16