1. Расчет линейной электрической цепи постоянного тока

Задание:

1. Рассчитать схему по законам Кирхгофа.

2. Определить токи в ветвях методом контурных токов.

3. Определить ток в ветви с сопротивлением R₁ методом эквивалентного      генератора.

4. Составить уравнение баланса мощностей и проверить его подстановкой      числовых значений.

5. Определить показания вольтметра.

Исходная схема:

Определения токов в ветвях по законам Кирхгофа

Зададим направления токов в ветвях и направления обхода контуров:

Определим количество уравнений по законам Кирхгофа:

N_{I З.К.} = 4 – 1 = 3

N_{II З.К.} = 6 – 4 + 1 = 3

Составим уравнения по законам Кирхгофа:

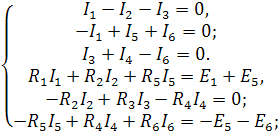
Метод контурных токов

Зададим направления токов в ветвях и направления обхода контуров

Рассчитаем токи в ветвях методом контурных токов:

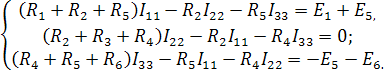
Подставим числовые значения сопротивлений и ЭДС и решим полученную систему уравнений в программе Gauss. Получим:

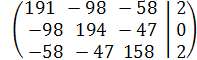
Определим значения токов в ветвях:

               

      

         

           

                   

Метод эквивалентного генератора

Преобразуем схему и определим значение напряжения холостого хода U_хх:

Составим систему уравнений, пользуясь методом контурных токов:

              

 

Подставим числовые значения сопротивлений и ЭДС и решим полученную систему уравнений в программе Gauss. Получим:

Рассчитаем напряжение холостого хода U_xx:

Преобразуем схему и найдем R_ЭГ:

=24,75257732 Ом

=23,74226804 Ом

=11,87113402 Ом

Определим ток в ветви с сопротивлением R_1:

Баланс мощностей:

0,12847 Вт =0,12847 Вт

Баланс мощностей сходится.

Определение показаний вольтметра:

2. Расчёт электрической цепи однофазного переменного тока

Задание:

1. Определить комплексные действующие значения токов в ветвях схемы.

2. Определить показания приборов.

3. Составить баланс активных, реактивных и полных мощностей.

4. Повысить коэффициент мощности до 0,98 включением необходимого реактивного элемента X.

5. Построить векторные диаграммы токов и напряжений в одной системе координат.

Исходная схема:

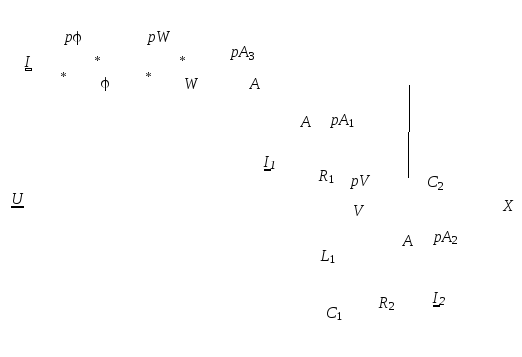
Дано: U = 100 В, F =100 Гц, R₁ = 88 Ом, R₂ = 10 Ом, L₁= 55 мГн, L₂ = 0 мГн, C₁ = 155 мкФ, C₂ = 110 мкФ.

Определение комплексных действующих значений токов в ветвях схемы

Частота источника, питающего сеть, F = 100 Гц. Определим частоту

Вычислим и найдем z:

Тогда

Z=

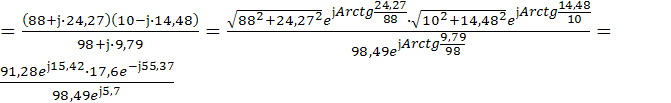=16,31 Ом

Z₁= Ом

Z₂= Ом

Определим входной ток с помощью закона Ома:

А

А

А

Определение показаний приборов

1) Показание амперметров

2) Показание вольтметра

pV=175,69 В

3) Показание фазометра

4) Показание ваттметра

Составление баланса активных, реактивных и полных мощностей

Запишем уравнение баланса мощностей:

Баланс мощностей соблюдается.

Повышение коэффициента мощности до 0,98 включением необходимого реактивного элемента X.

Отсюда:

G=0,042

b_C=0,043

Тогда

Построение векторных диаграмм токов и напряжений в одной системе координат

В

В

MI: 0,1A:1см                                                                                   MU: 2В:1см

3. Расчёт трёхфазной цепи

Задания:

1. Составить схему включения приёмников.

2. Определить комплексы действующих значений фазных и линейных токов.

3. Составить схему включения ваттметров для измерения активной мощности каждого трёхфазного приёмника.

4. Рассчитать активную, реактивную и полную мощность каждого приемника.

5. Построить векторные диаграммы токов и напряжений для каждого приемника.

Исходная схема:

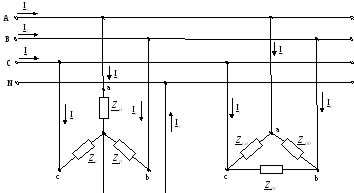
Схема соединения приемников: звезда. Дано: нагрузка: симметричная, U = 220 В, R = 142Ом, L = 8 мГн.

Схема соединения приемников: треугольник. Дано: нагрузка: несимметричная, U = 220 В, R_ab = 133 Ом, R_bc = 56 Ом, R_ca = 0 Ом, L_ab = 0 мГн, L_bc = 0 мГн, L_ca = 127 мГн, C_ab = 143 мкФ, C_bc = 139 мкФ, C_ca = 0 мкФ.

Схема соединения «звезда»

1. Схема включения приёмников:

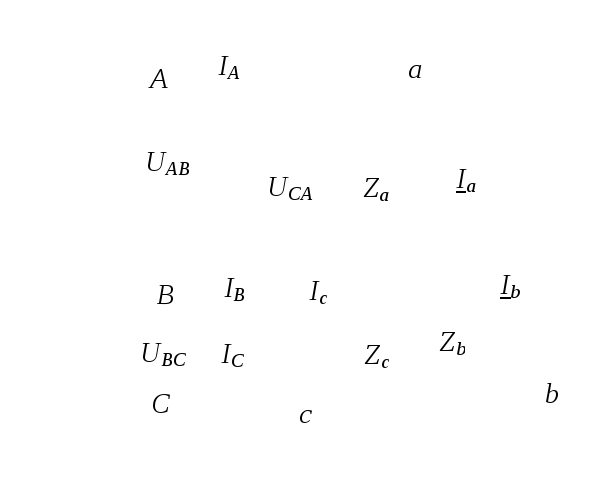
2) Определение комплексов действующих значений линейных токов

Рассчитаем фазные напряжения:

В

B

B

Представим фазные напряжения в алгебраической форме:

В

B

B

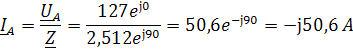
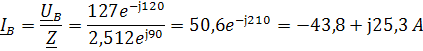
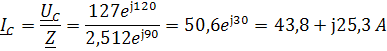
Схема включения ваттметра для измерения активной мощности каждого трёхфазного приёмника:

Показания ваттметра:

Активная мощность приемников:

Реактивная мощность приемников:

Полная мощность приемников:

Векторные диаграммы токов и напряжений

M_I: 1A:1см M_U: 6В:1см

Схема соединения «треугольник»

1. Схема включения приёмников:

2. Рассчитаем фазные напряжения:

В

B

B

3. Комплексы полных сопротивлений приемников:

Ом

Ом

Ом

4. Определим комплексы фазных токов по закону Ома:

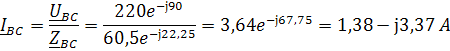
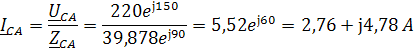
Определим комплексы линейных токов по первому закону Кирхгофа:

Схема включения ваттметров для измерения активной мощности каждого трёхфазного приёмника:

Показания ваттметров:

Активная мощность приемников:

Реактивная мощность приемников:

Полная мощность приемников:

Векторные диаграммы токов и напряжений:

M_I: 10A:1см M_U: 6В:1см

12081.253069.000