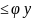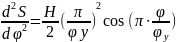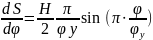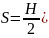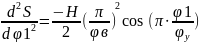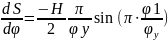2.2. Проверки качества зубьев и зацепления

Проверка передачи на прочность

Работа передачи будет плавной, если коэффициент перекрытия ε будет не меньше 1,115. У нас ε = 1,2 что больше допустимого.

Проверка на незаострение Sa≥0,4m

Sa₁≥0,4m Sa₂≥0,4m

1.376≥1,2 2.194≥1,2

Зубья незаострены

Проверка на отсутствие подрезания 0,5Zsin²α≥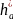 – x

0,5Z₁sin²α≥ – x₁ 0,5Z₂sin²α≥ – x₂

0,5·12·sin²20° ≥ 1 – 0,574 0,5·28·sin²20° ≥ 1 – 0,482

0.7018 ≥ 0,426 1.6376 ≥ 0,518

2.3. Вычисление контрольных размеров, проставляемых на чертеже

Размер по постоянной хорде.

Расположим обкатывающую рейку симметрично полюса станочного зацепления и опустим из полюса перпендикуляры на профиль, чтобы получить точки. В и М касания контура с профилем зуба.

Отрезок, соединяющий эти точки, называется постоянной хордой.

Длина ее обозначается Sc.

S_C1 = S₁·cos²α = 5,966 · 0,93969² = 5,268 мм

S_C2 = S₂·cos²α = 5,765 · 0,93969² = 5,091 мм

Расстояния от окружности вершин до постоянной хорды

h_c1 = r_a1 – r₁ – 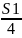· sin2α = 22,311 – 18 – 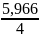· 0,64279 = 3,352 мм

h_c2 = r_a2 – r₂ – 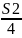· sin2α = 46,035 – 42 – 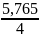· 0,64279 = 3,109 мм

Длина общей нормали.

Длина общей нормали W измеряется скобой. Сначала нужно определить число впадин, охватываемых скобой, из условия, чтобы скоба касалась профилей в эвольвентной их части. Обычно по обе стороны от делительного цилиндра имеется эвольвентный участок профиля, поэтому берут такое число охватываемых зубьев, при котором скоба соприкасается с ними далеко от делительного цилиндра.

При касании скобы с профилями на делительном цилиндре охватываемый ей центральный угол равен 2α. Тогда число шагов, охватываемых скобой (число впадин):

n₁ = 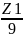= = 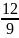1

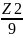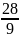n₂ = = = 3

По свойству эвольвенты длина общей нормали равна длине дуги между началами эвольвент на основной окружности. Поэтому при числе n охватываемых впадин длина общей нормали равна:

W₁ = P_bn₁ + S_b1 = 8,856 · 1 + 6,110 = 17,92 мм

W₂ = P_bn₂ + S_b2 = 8,856 · 3 + 6,594 = 34,15 мм

3. Проектирование и исследование планетарного механизма

3.1. Подбор чисел зубьев колес планетарного механизма

По исходным данным определяем Z3, Z4, Z5, Z6. Определяем передаточное отношение U3-H

U_3-H = 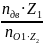= = 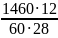10,43

Определяем угловую скорость центрального колеса 3 планетарного механизма:

ω_дв = 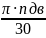= = 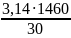152,81 рад/с

ω₂ = ω₃ = ω_дв · 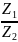= 152,81 · 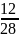= 65,49 рад/с

По этим данным по компьютерной программе получаем таблицу возможных вариантов, представленных в таблице 3.1. При подборе чисел зубьев используем 3 условия:

1. Условие соосности;

2. Условие соседства;

3. Условия сборки.

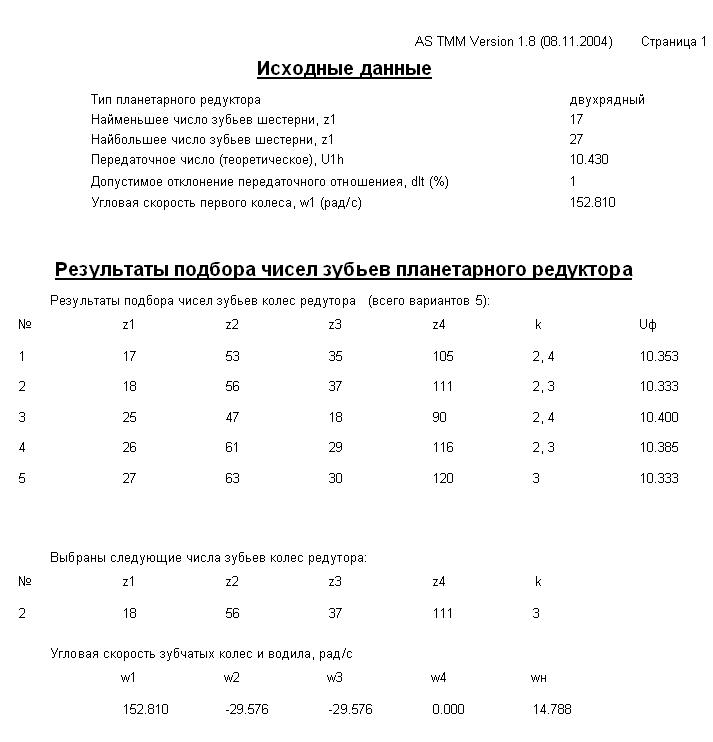
Таблица 3.1 – Результаты подбора чисел зубьев планетарного редуктора

4. Проектирование кулачкового механизма

4.1. Расчет законов движения толкателя и построение графиков

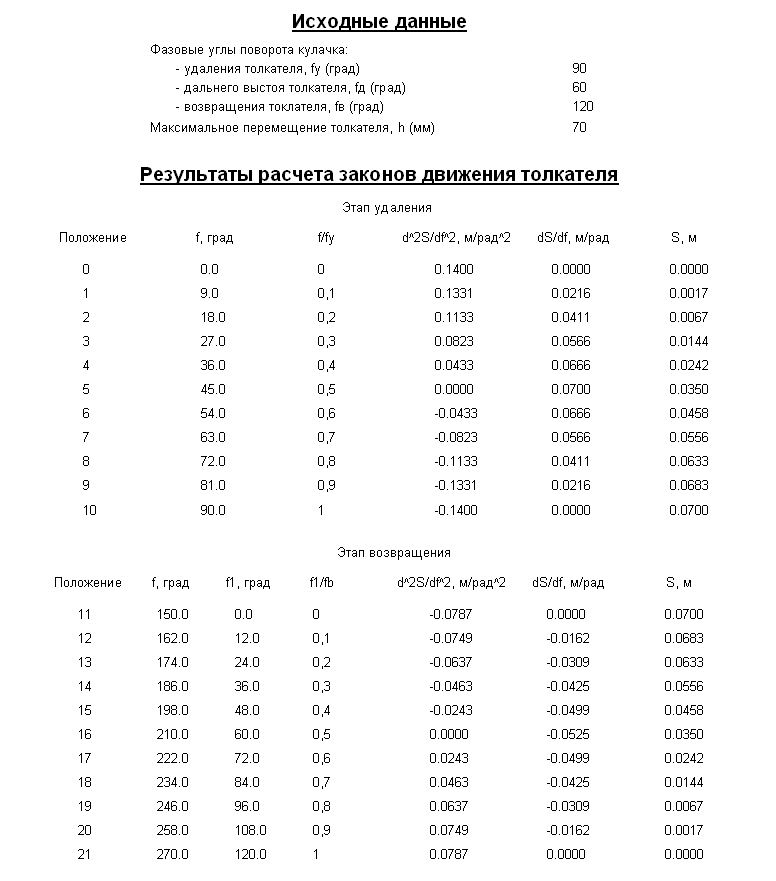
Исходные данные для расчета законов движения толкателя:

h	70
e	10
γmin	55
φвід.	90
φв.в	60
φнаб.	120

Минимальный радиус центрового профиля кулачка r0 = 60 мм. Закон изменения аналога ускорения, скорости и перемещения толкателя представлены в таблице 4.1. Производим расчет этих законов, используя программу (см. табл. 4.2.)

Таблица 4.1 Аналитическое выражение законов перемещения, аналогов скоростей и ускорений толкателя

На этапе удаления	На этапе возвращения
0 φ	0 φ1

Результаты расчета законов движения толкателя представлены в таблице 4.2.

Строим графики углового перемещения толкателя, аналога скорости и аналога ускорения толкателя в функции угла поворота кулачка, приняв следующие значения масштабных коэффициентов:

μ_φ = 1 град/мм

μ_S = 0,002 м/мм

μdS/dt = 0,002 ·6,28 = 0,0125

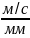
μd²S/dt = 0,002 ·6,28² = 0,0789

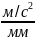
Таблица 4.2 – Результаты расчета законов движения толкателя

(этап удаления)