Построение планов скоростей и планов ускорений
Построение планов механизма. Принимаем μl = 0,005 м /мм и строим 12 положений планов механизма. Длины звеньев на чертеже:
О1А = lO1A /μl = 0,135 / 0,005 = 26 мм
АВ = lAB /μl = 0,665 / 0,005 = 128 мм
O2C = l O2C /μl = 0,630 / 0, 005 = 121.3 мм
O2B = l O2B /μl = 0,450 /0,005 = 86.7 мм
Строим план скоростей
Расчеты скоростей для двух положений механизма.
Определяем ω1:
ω1
=
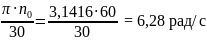
Принимаем (Pva) = 84.8 мм, тогда масштабный коэффициент
μV
= 0,01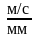
Нулевое положение.
Va0 = ω1·lO1A0 = 6,28·0,135 = 0,848 м/с
VB0 = VC0 = 0, т.к. это крайнее правое положение этих точек.
Первое положение (α = 30˚)
VА = ω1 · l01A =6,28 · 0,135=0,848 м/с
Скорость точки B определяем графически
VB = VА + VB-A , где VB-A = (ab)·μV = 0,1782 м/с
VB = PVB · μV = 70,67 · 0,01 = 0,7067 м/с
Скорость точки С определяем по теореме подобия, составим пропорцию:
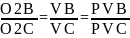
VC3
=
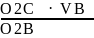= 0,630 ·
0,7067 / 0,450 = 0.989 м/с
Vc5 находим графически опустив из конца Vc3 перпендикуляр на горизонтальную линию выходящую из полюса PV.
Угловые скорости звеньев:
ω2
=
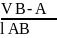= 0,1782 / 0.665
= 0,27 рад/с
ω3
=
=
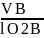0,7067 / 0,450 = 1,57 рад/с
Построение планов ускорений.
Планы ускорений строим тоже для двух положений: нулевого и первого заданного.
Для нулевого:
Ускорение точки А:
aA0 = aA0n + aA0τ , где
aA0n = ω2 · lO1A0 = 6,28 · 0,135 = 5,324 м/с2
aA0τ = ε1 · lO1A0 = 0 , т.к. ε1 = 0
Принимаем Pаa = 106,5 мм, тогда:
μa
= 0,05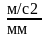
Ускорение точки B и С:
aB0 = aC0 = 0 м/с2
Для первого 30˚:
Ускорение точки А:
aA = aAn + aAτ , где
aAn = ω2 · lO1A = 6,28 · 0,135 = 5,324 м/с2
aAτ = ε1 · lO1A = 0 , т.к. ε1 = 0
Принимаем Pаa = 106,5 мм, тогда:
μa = 0,05
Ускорение точки В:
aB = aA+aB-An + aB-Aτ, где
aB-An
=
=
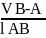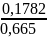= 0,26 м/с2
aBn
=
=
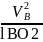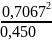= 1,11 м/с2
Угловые ускорения звеньев:
Положение №1 α=30°
ε2
=
=
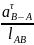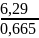= 9,46 рад/с2
ε3
=
=
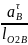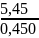= 12,11 рад/с2
Нулевое положение
ε2 = = = 9,46 рад/с2
ε3 = = = 12,11 рад/с2
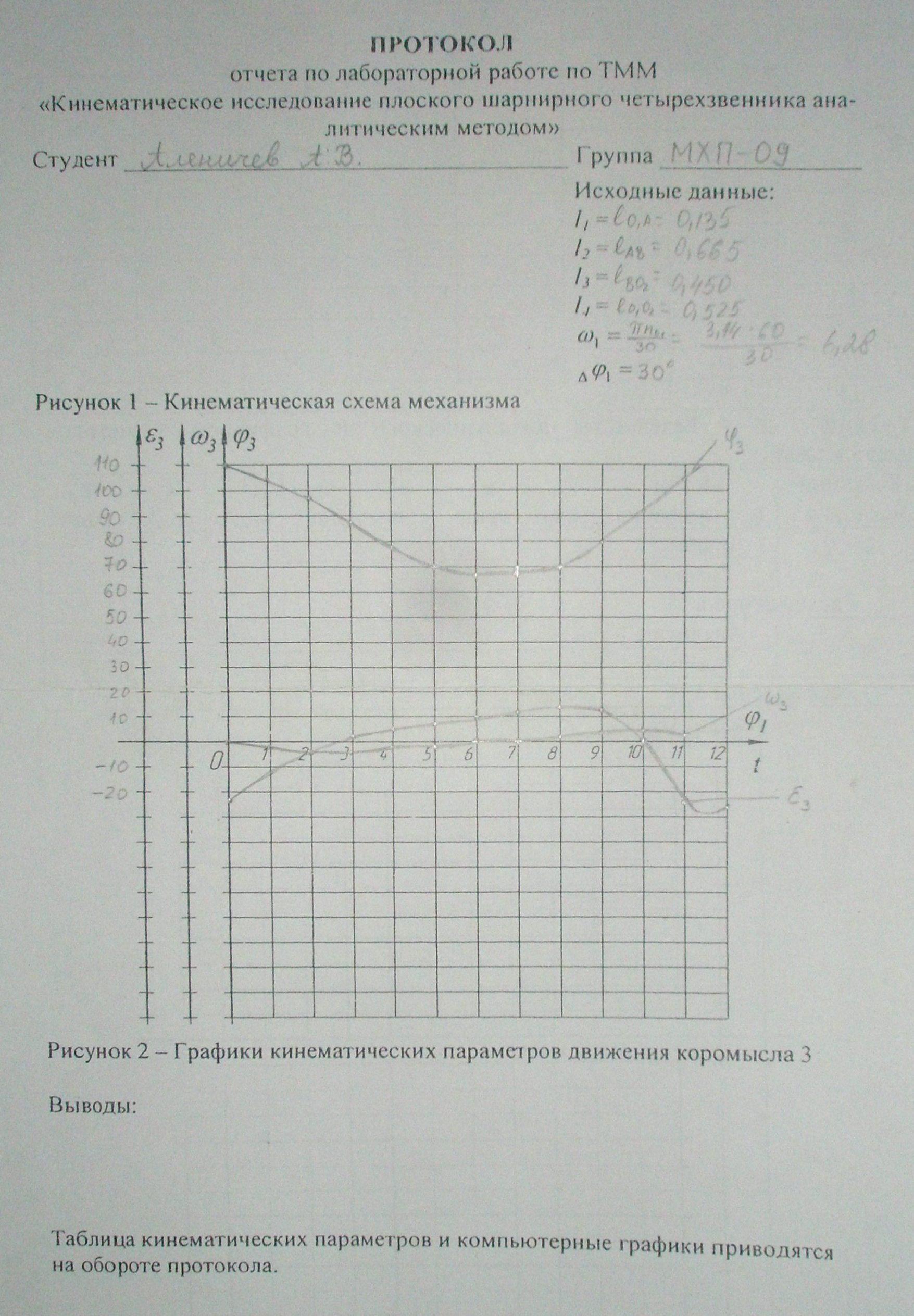
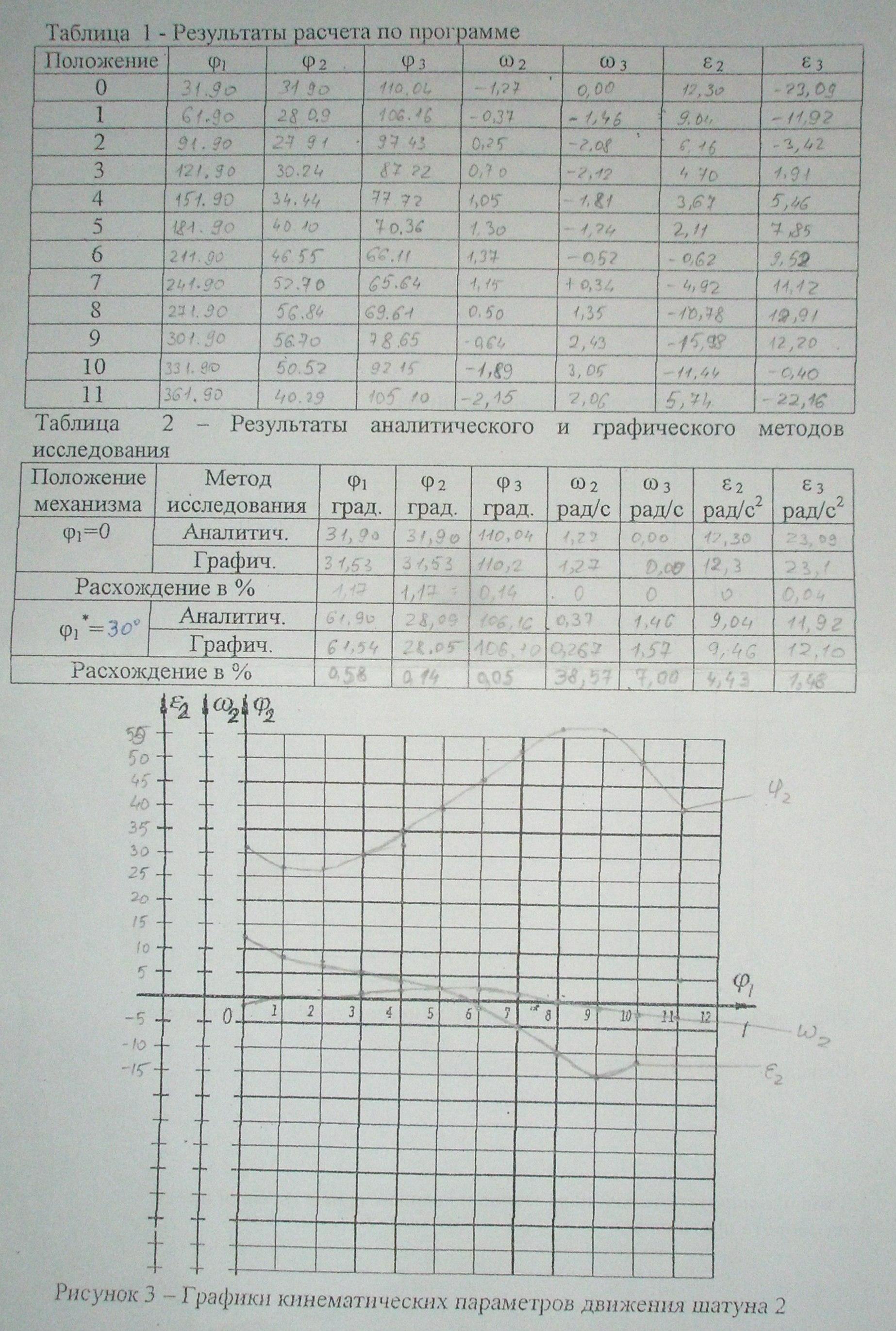
1.3. Аналитический расчет кинематических параметров
Для того чтобы сравнить значения кинематических параметров движения звеньев 2 и 3 полученных графическим методом со значениями аналитического метода в курсовом проекте использованы ЭВМ.
Исходные данные
к аналитическому расчету:
,
,
,
,
.
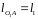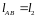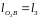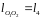Угол
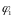– обобщённая координата механизма,
которая определяет положение кривошипа.
Необходимо
определить углы
,
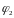и
,
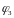которые определяют положение кривошипа
1, шатуна 2 и коромысла 3, угловые скорости
этих звеньев
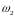и
,
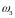их угловые ускорения
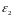и
.
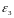Векторный контур, образованный звеньями механизма (рис. 1.2), можно показать уравнением:
.
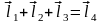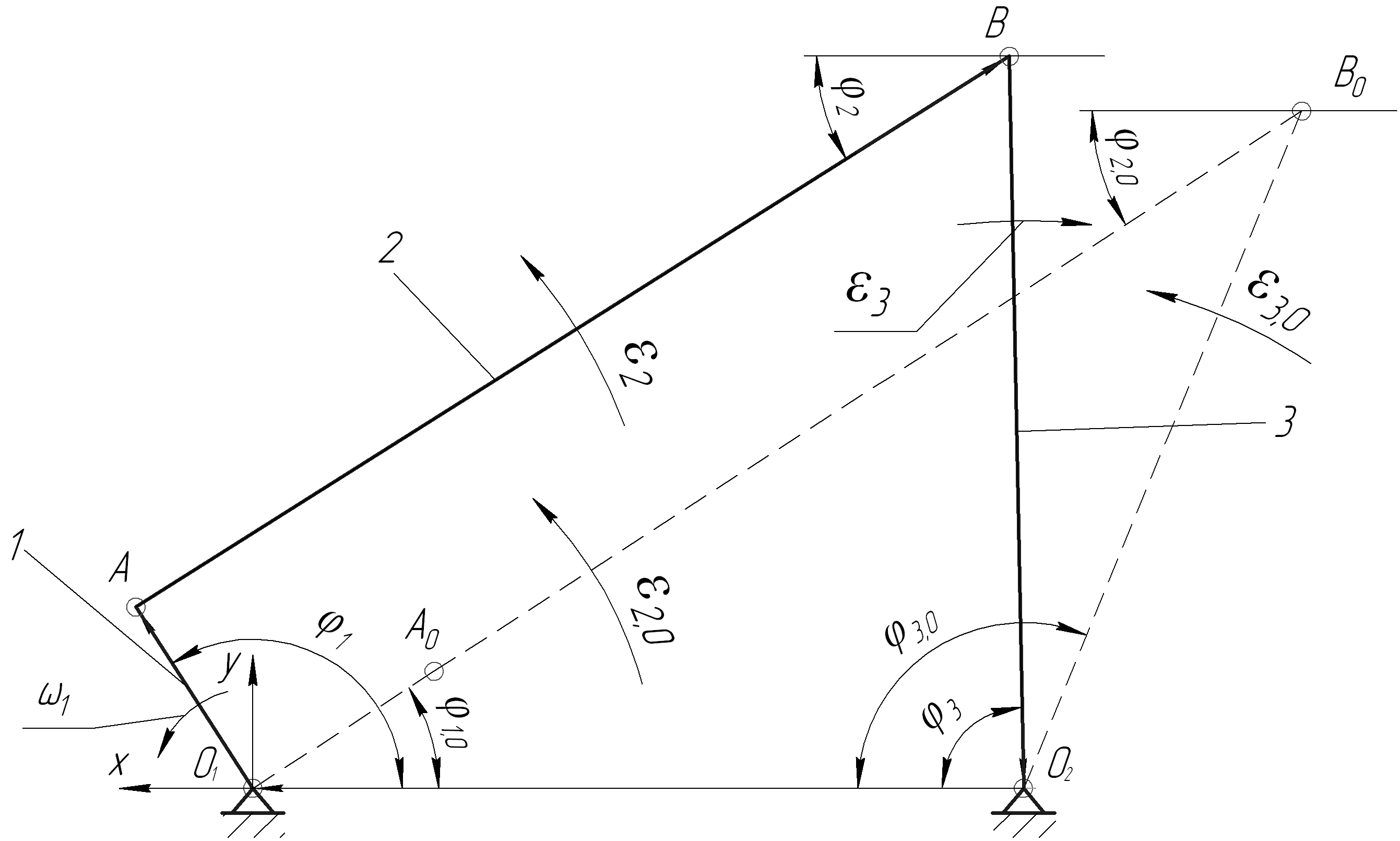Рисунок
1.2 – Схема рычажного
механизма
в аналитическом методе
Спроецировав полученное ранее векторное уравнение на оси x и y, получаем:
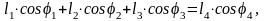
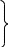
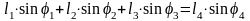
Так как
,
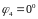то
,
.
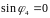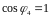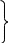Обозначаем
известные величины:
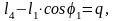
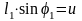
Тогда получаем:
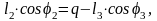
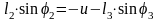
Для удобства введём обозначения:
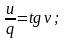
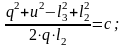
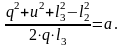
Тогда, после соответствующих замен, получаем:
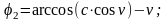
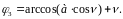
Угловые скорости и ускорения звеньев 2 и 3 определяем, взяв первую производную по времени t и выполнив необходимые преобразования:
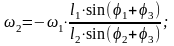
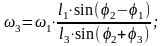
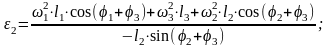
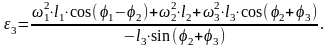
По приведенному выше алгоритму программа вычисляет значения кинематических параметров движения звеньев 2 и 3, и строит их графики.
