
- •Лабораторная работа № 1 Тема: Создание, редактирование и форматирование документа в Word Содержание лабораторной работы
- •Контрольные вопросы
- •Лабораторная работа № 2 Тема: Работа с таблицами в Word. Набор и редактирование математических формул Содержание лабораторной работы
- •Контрольные вопросы
- •Лабораторная работа № 3 Тема: Вычисления по формулам в Excel Содержание лабораторной работы
- •Контрольные вопросы
- •Лабораторная работа № 4 Тема: Работа с мастером формул в Excel Содержание лабораторной работы
- •Контрольные вопросы
Лабораторная работа № 4 Тема: Работа с мастером формул в Excel Содержание лабораторной работы
Задание 1. Выполнить по вариантам следующие задания с использованием Мастера функций.
Дано натуральное число n, действительные числа а1,...,аn . Получить
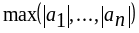 и
и
 .
.Дано натуральное число n, действительные числа а1,...,аn . Получить
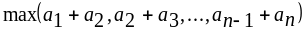 и
и
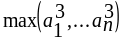 .
.Дано натуральное число n, действительные числа а1,...,аn . Получить
 .
.Дано натуральное число n, действительные числа а1,...,аn . Получить
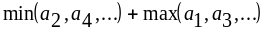 .
.Дано натуральное число n, действительные числа а1,...,аn. Получить: а)
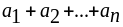 ;
б)
;
б)
 ;
;
в)
среднее арифметическое чисел а1,...,аn
; г)
![]()
Даны действительные числа x, y, z. Вычислить :
а)
![]() ;
б)
;
б)
![]() .
.
Даны действительные x, y, z. Вычислить :
a)
![]() ;
б)
;
б)
![]() .
.
Даны действительные числа y1, y2 ,..., y12 .
Найти
![]() , где
, где
![]()
Даны действительные числа y1, y2 ,..., y15 .
Найти
![]() , где
, где
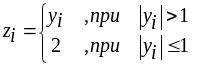
Даны действительные числа y1, y2 ,..., y10 .
Найти
![]() , где
, где
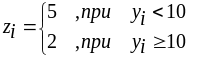
Пусть a0=cos21 , a1= -sin21 , где
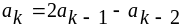 ,
k=2,3,...,15.
Найти
сумму квадратов тех чисел a1,
a2
,..., a15
, которые не превосходят двух.
,
k=2,3,...,15.
Найти
сумму квадратов тех чисел a1,
a2
,..., a15
, которые не превосходят двух.Пусть
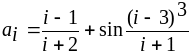 ,
где i=1,2,...14.
Найти все положительные числа, среди
положительных a1,
a2
,..., a14
выбрать наименьшее число.
,
где i=1,2,...14.
Найти все положительные числа, среди
положительных a1,
a2
,..., a14
выбрать наименьшее число.Даны действительные x, y . Вычислить z:
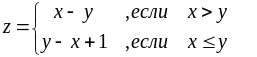
Дано натуральное число n, действительные числа а1,...,аn . Получить: а)
 ; б)
; б)
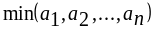 ;
;
в)
![]() ; г)
; г)
![]() +
+
Вычислить
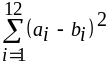 ,
где
,
где
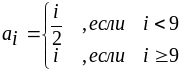
![]()
Дано натуральное число n. Найти наибольшее среди чисел
 k=1,…,n
, а также сумму всех этих чисел.
k=1,…,n
, а также сумму всех этих чисел.Даны натуральное число n, действительные числа х1,...,хn . Получить (1+r)/(1+s), где r – сумма всех тех членов последовательности х1,...,хn , которые не превосходят 1, а s – сумма членов, больших 1.
Даны действительные числа y1, y2 ,..., y10 .
Найти
![]() ,
где
,
где
![]()
Задание 2. Необходимо создать отчетную ведомость по расчету затрат на производство товара. Пусть фирма производит какой-либо товар. Упаковка товара обходится фирме в 1 грн/шт., стоимость материала – 4 грн/шт. Готовый товар фирма продает по цене 10 грн/шт. Технические возможности фирмы позволяют выпускать до 5 тысяч товара в день. Оплата труда рабочих является сдельной и зависит от количества выпущенного товара. За первую тысячу товара оплата труда рабочих составляет 0,3 грн/шт., за вторую тысячу товара – 0,4 грн/шт., за третью тысячу товара – 0,5 грн/шт., четвертую тысячу товара – 0,6 грн/шт. и свыше 4000 товара – 0,7 грн/шт.
Фирме поступил заказ на изготовление 300*N штук товара (N - номер варианта). Необходимо подсчитать суммарные издержки и прибыль от выполнения данного заказа. В графе «Оплата, грн» необходимо рассчитать заработную плату в зависимости от заказанной партии, при этом суммарную оплату переносят в строку «Зарплата». «Стоимость упаковки» и «Стоимость материала» рассчитывают исходя из партии заказа и соответствующей стоимости, приходящейся на 1 шт. Прибыль вычисляют как разницу между стоимостью продажи и суммарными издержками.
Контрольные вопросы
1. Опишите синтаксис функции?
2. Какие категории функций Вы знаете?
3. Что такое Мастер функций?
4. Как создать формулу с использованием Мастера функций?
5. Что такое вложенные функции? Приведите примеры.
6. Как работают логические функции?
Лабораторная работа № 5
Тема: Построение диаграмм в Excel
Содержание лабораторной работы
По вариантам построить: 1) в разных системах координат графики функций; 2) в одной системе координат графики функций; 3) поверхность.
Вариант 1
х[-2;2] а)
 б)
б)
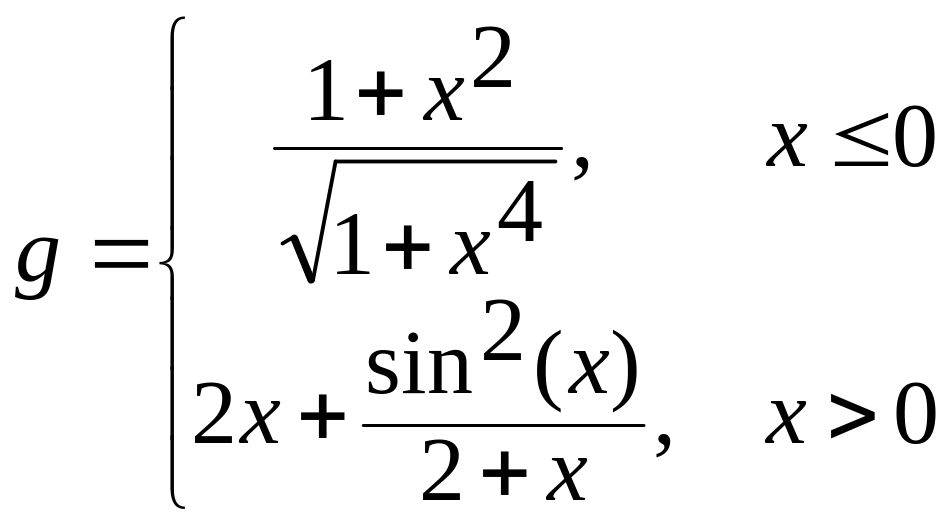
в) ![]()
2. х[-2;2] ![]() и
и ![]()
3. Построить
поверхность
![]() при х,y[-1;1]
при х,y[-1;1]
Вариант 2
х[-2;2] а)

б)
 в)
в)
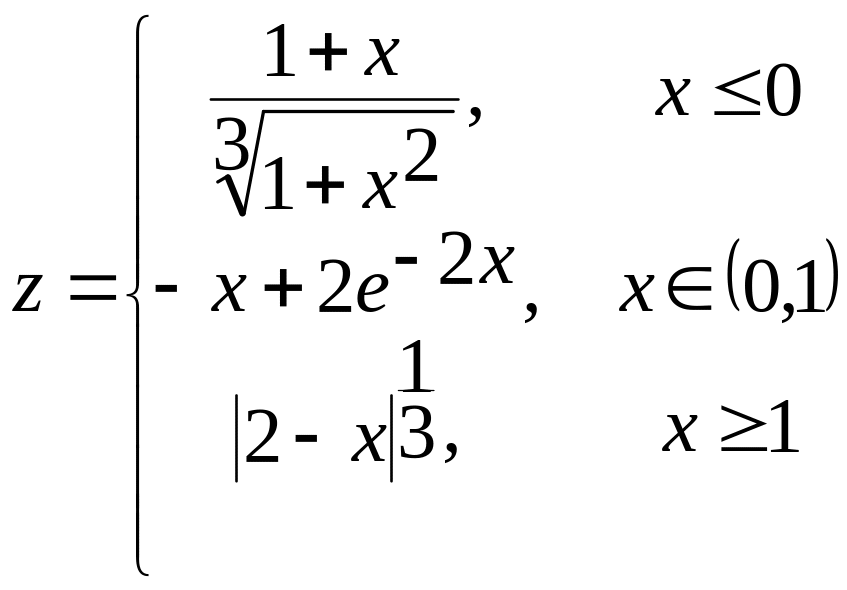
2. х[-2;2] ![]() и
и ![]()
3. Построить
поверхность
![]() при х,y[-1;1]
при х,y[-1;1]
Вариант 3
1. х[-2;1,5] а) 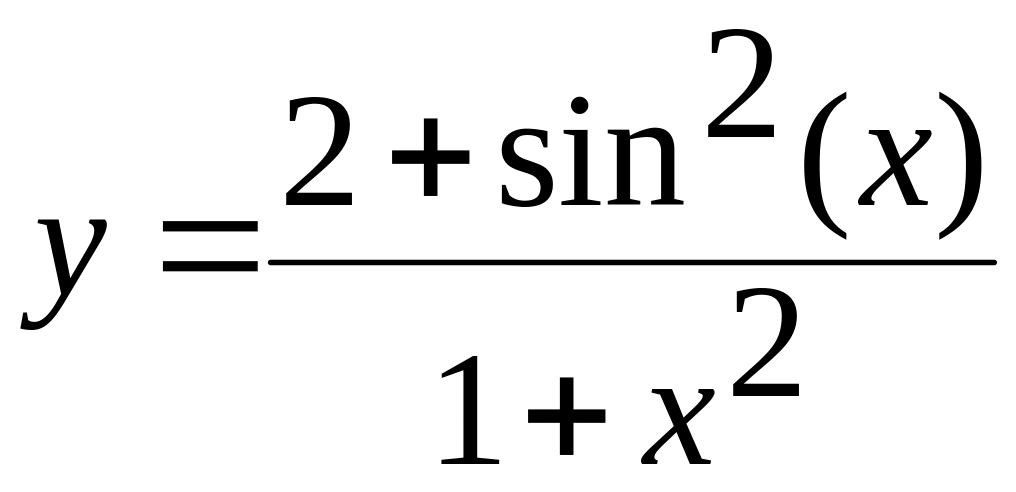
б) 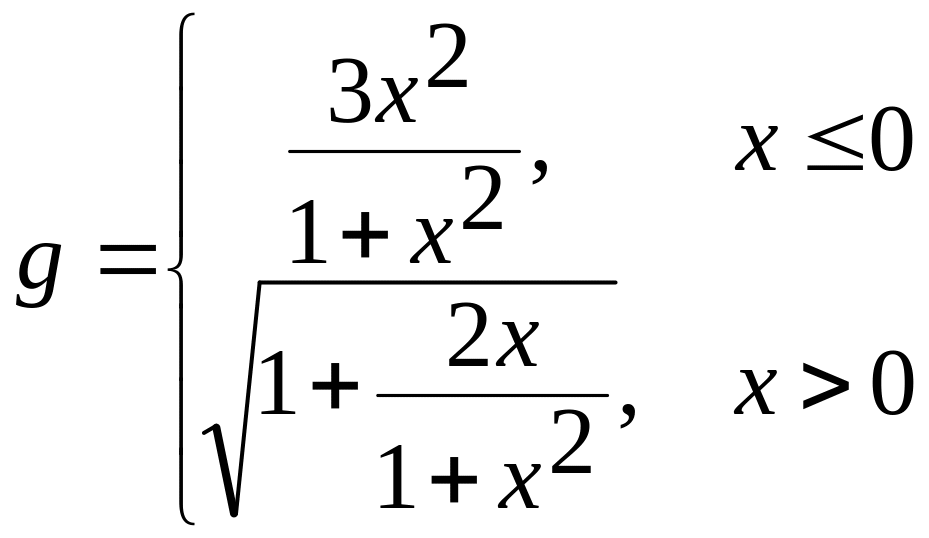 в)
в) 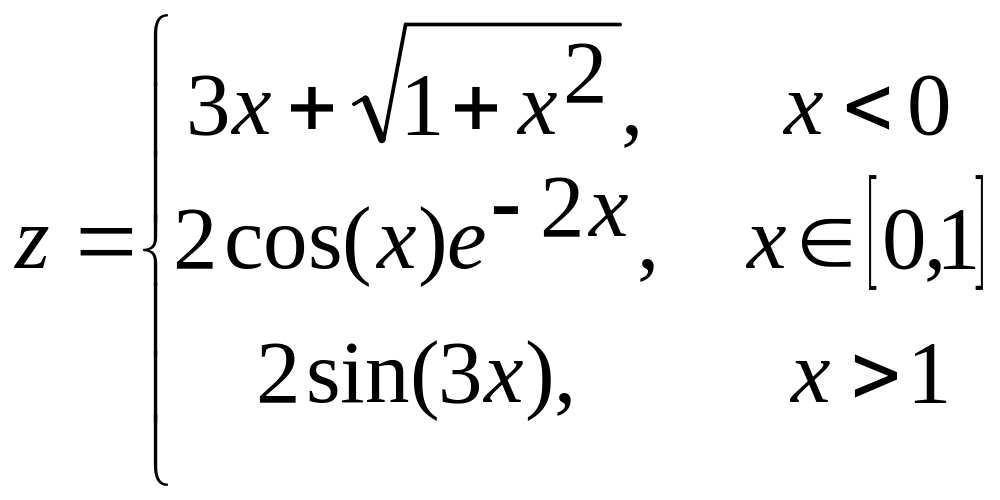
2. х[-2;2] ![]() и
и
![]()
3. Построить
поверхность
![]() при х,y[-1;1]
при х,y[-1;1]
Вариант 4
1. х[-1,5;1,5] а) 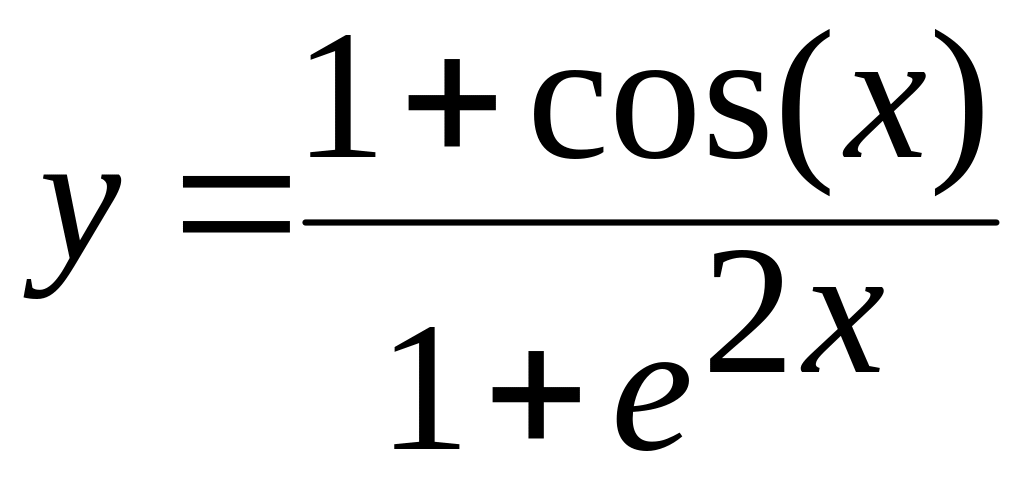
б) 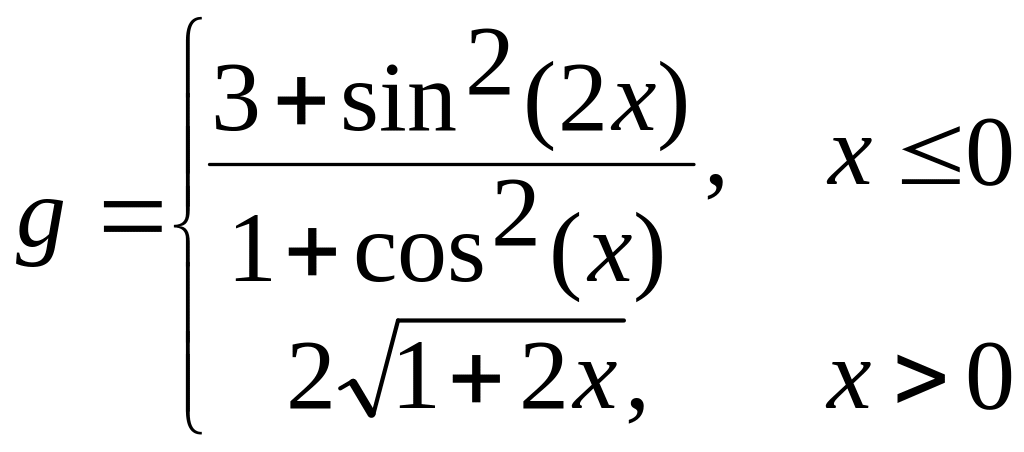 в)
в) 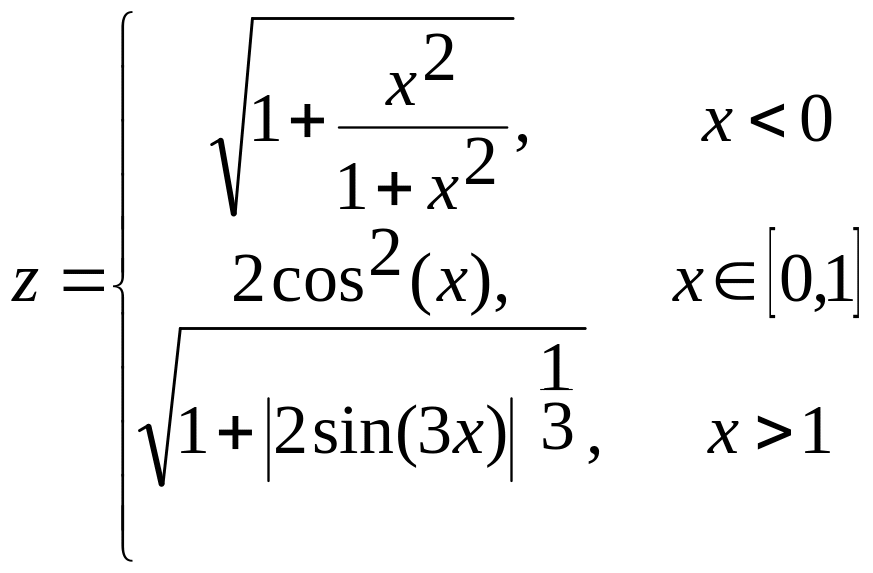
х[-2;2]
 и
и
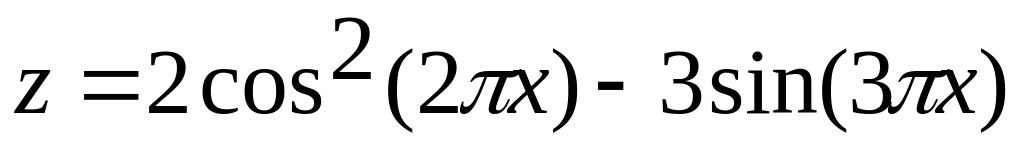
3. Построить поверхность при х,y[-1;1]
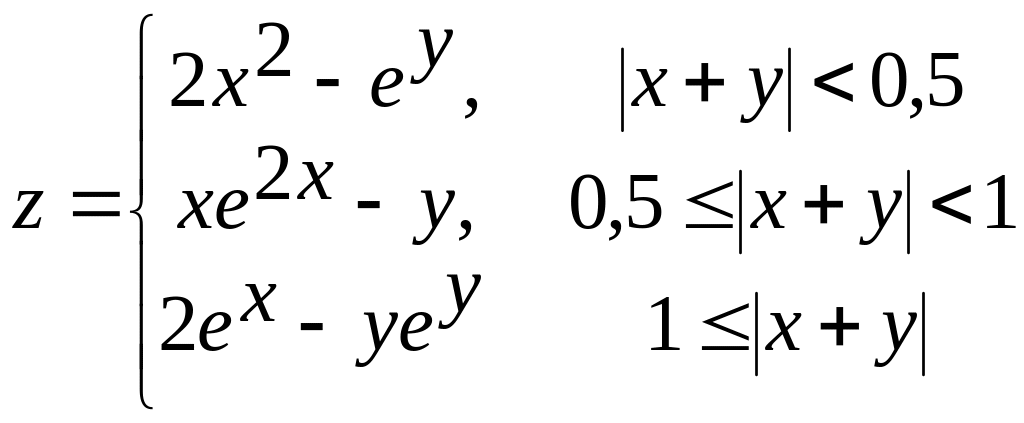
Вариант 5
1. х[-1,8;1,8] а) ![]()
б) 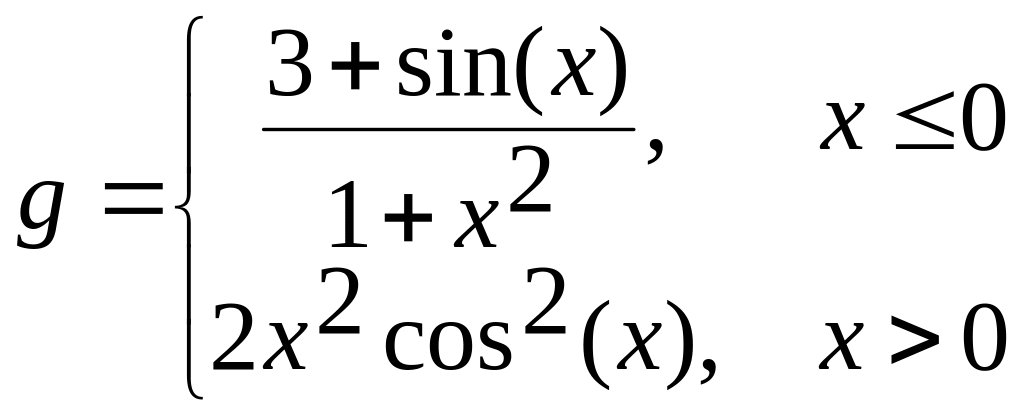 в)
в) 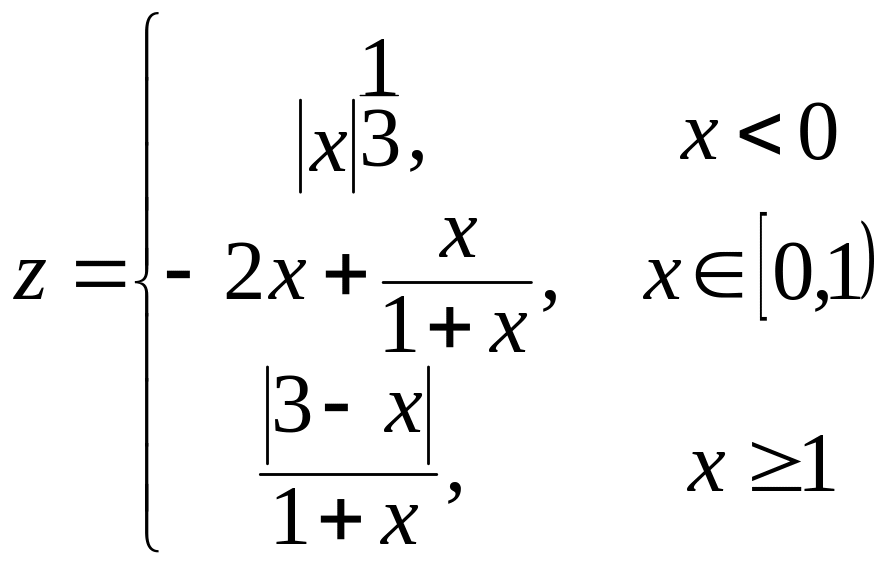
2. х[0;3] ![]() и
и ![]()
3. Построить
поверхность
![]() при х,y[-1;1]
при х,y[-1;1]
Вариант 6
1. х[-2;1,8] а) ![]()
б) 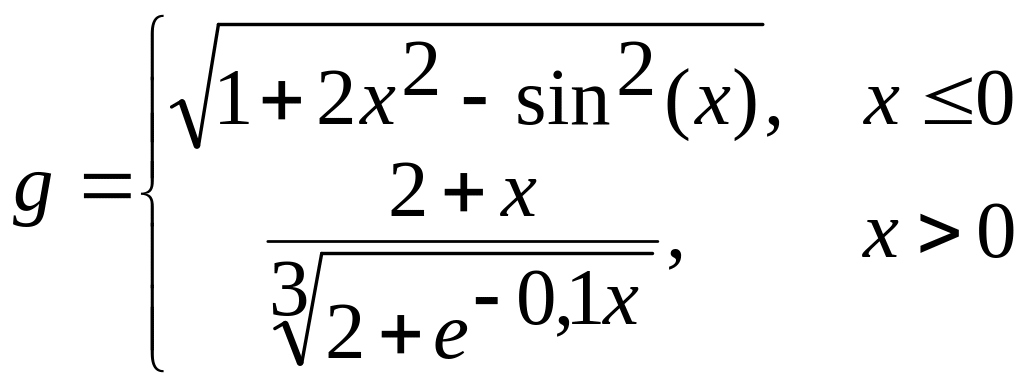 в)
в) 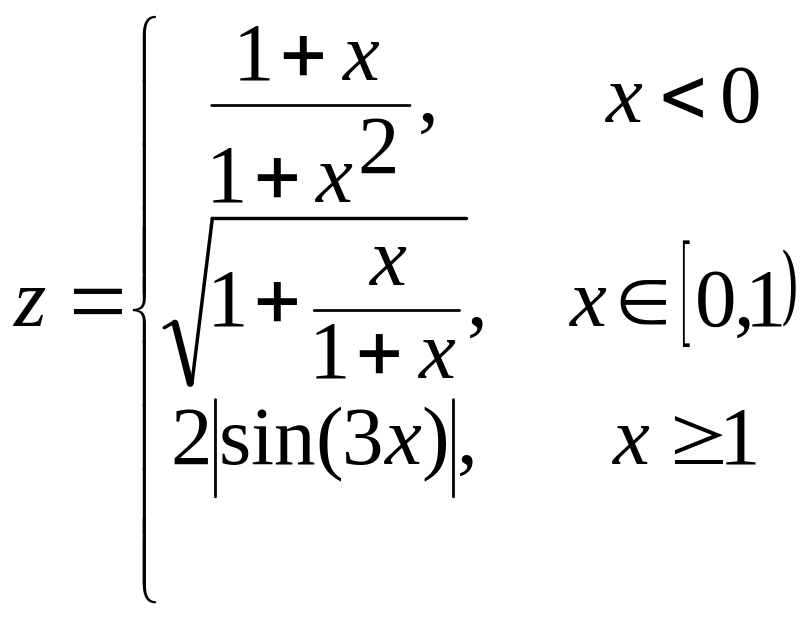
2. х[-3;0] ![]() и
и ![]()
3. Построить
поверхность
![]() при х,y[-1;1]
при х,y[-1;1]
Вариант 7
х[-1,7;1,5] а)
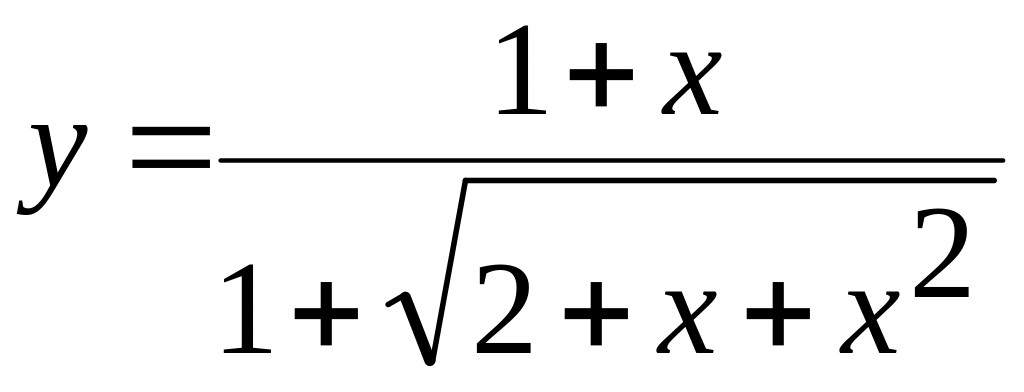
б) 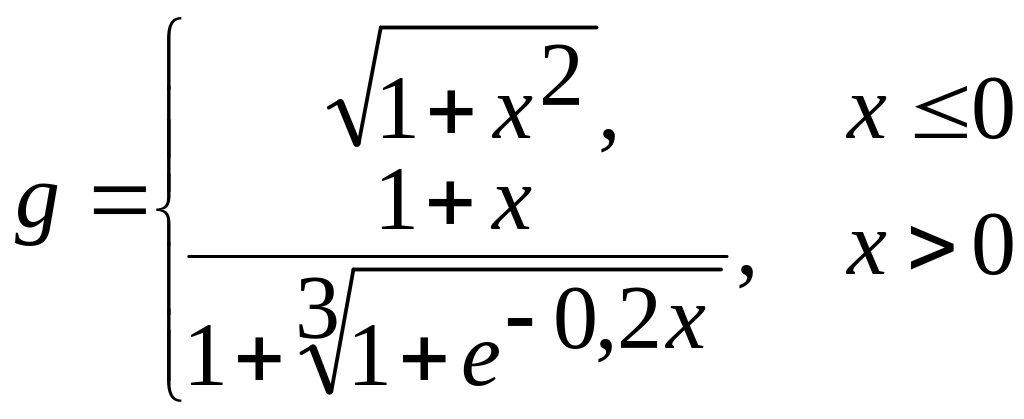 в)
в) 
2. х[-3;0] ![]() и
и ![]()
3. Построить
поверхность
![]() при х,y[-1;1]
при х,y[-1;1]
Вариант 8
1. х[-1,5;1,8] а) 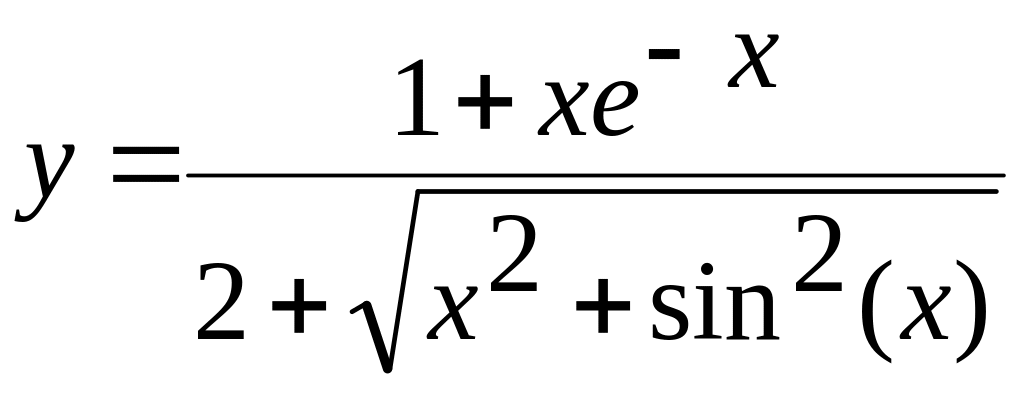
б) 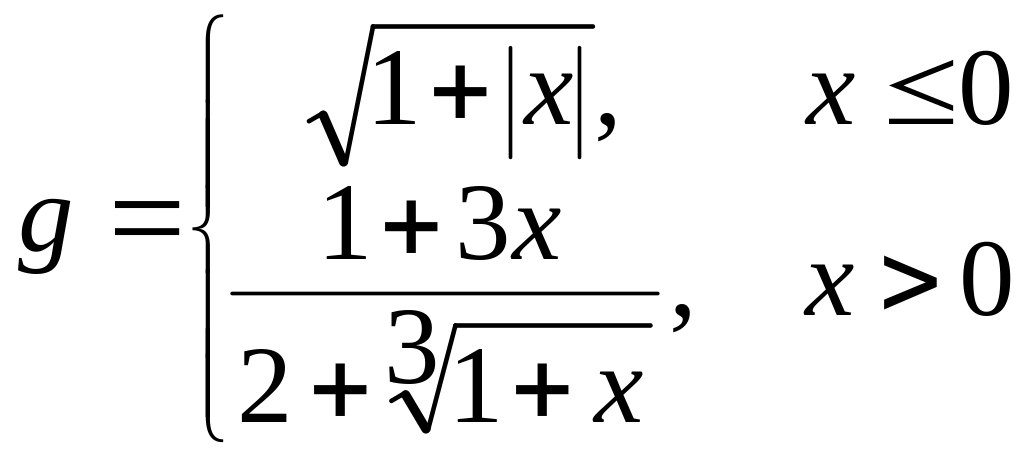 в)
в) 
х[0;2]
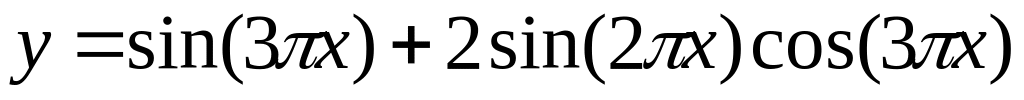 и
и
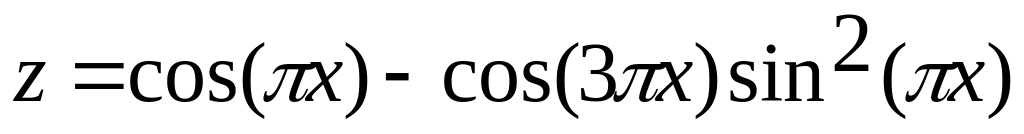
3. Построить
поверхность
![]() при х,y[-1;1]
при х,y[-1;1]
Вариант 9
1. х[-1,4;1,9] а) 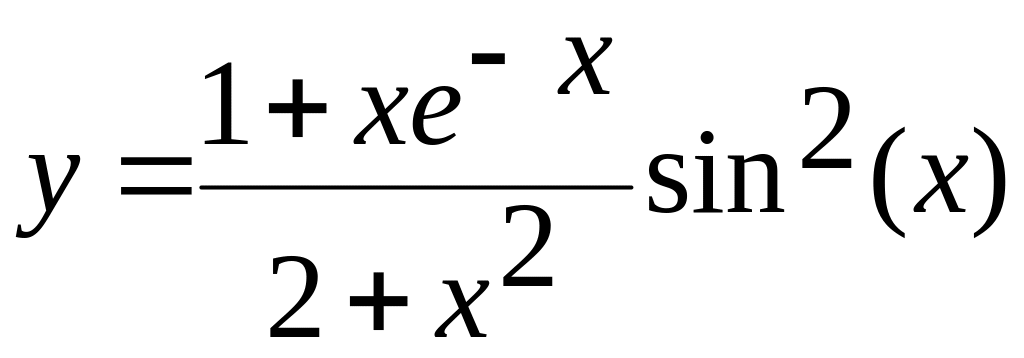
б) 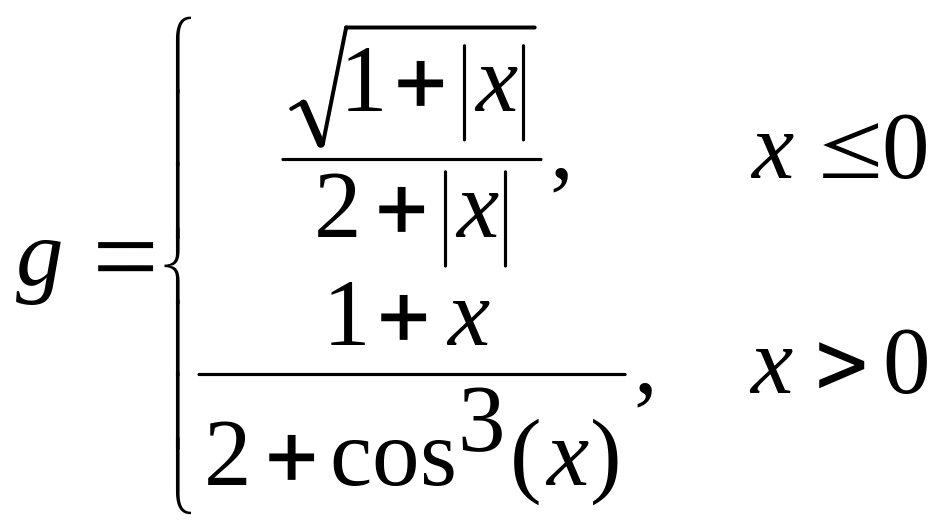 в)
в) 
2. х[0;2]
![]() и
и
![]()
3. Построить
поверхность при х,y[-1;1]

Вариант 10
х[-1,4;1,4] a)
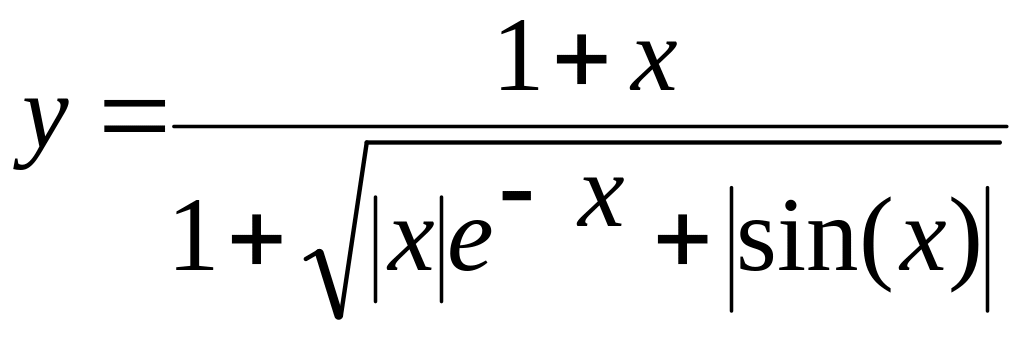
б) 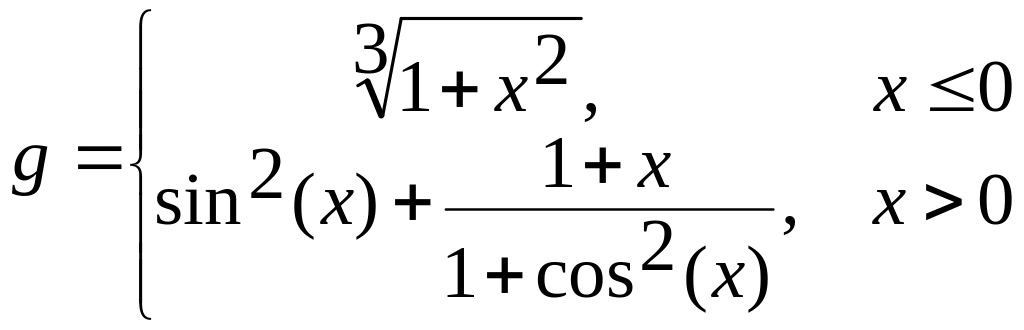 в)
в) 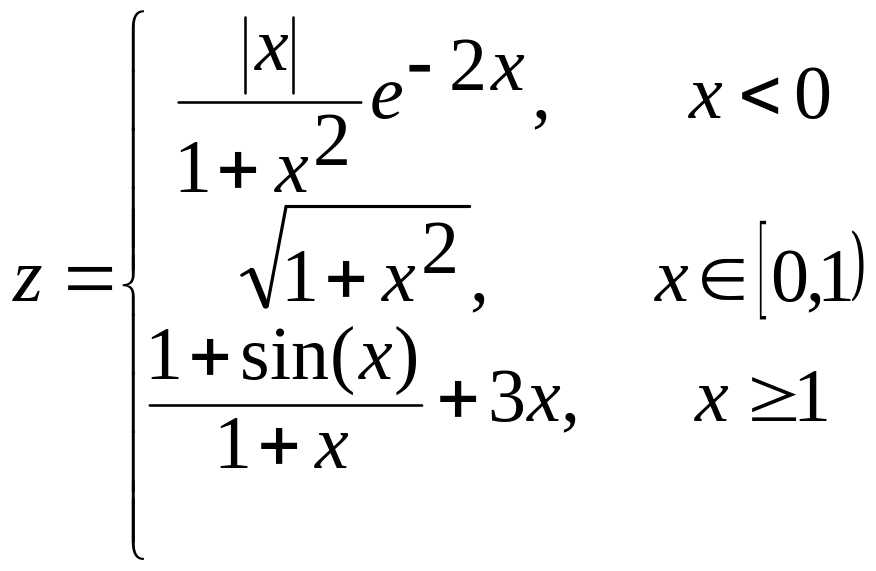
х[0;2]
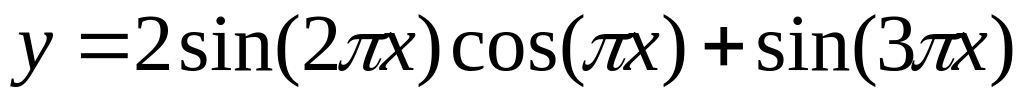 и
и
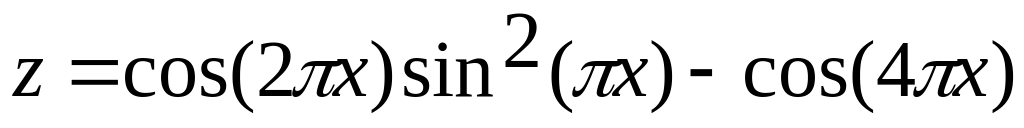
Построить поверхность при х,y[-1;1]
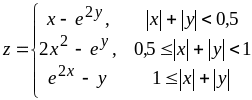
Вариант 11
1. х[-2;2] а)
б) в)
2. х[-2;2] и
3. Построить поверхность при х,y[-1;1]
Вариант 12
1. х[-2;1,8] а) 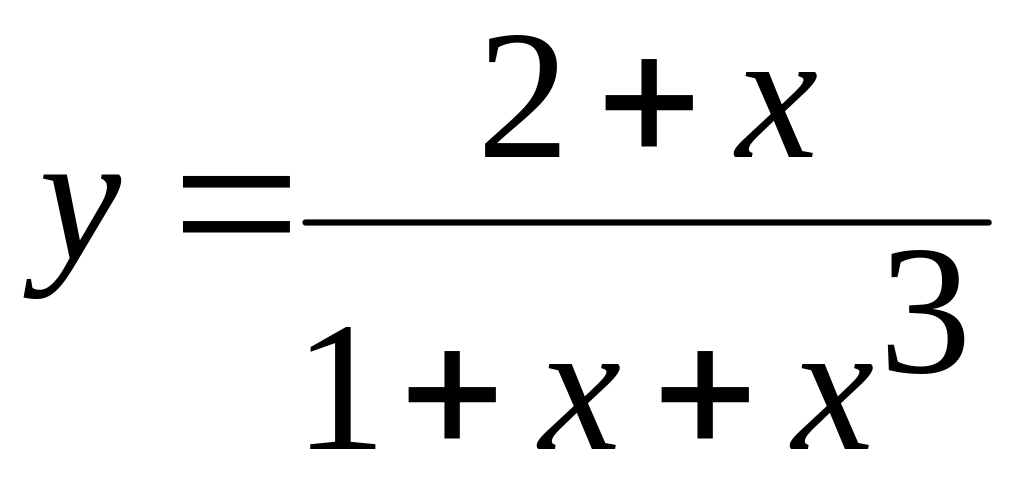
б) 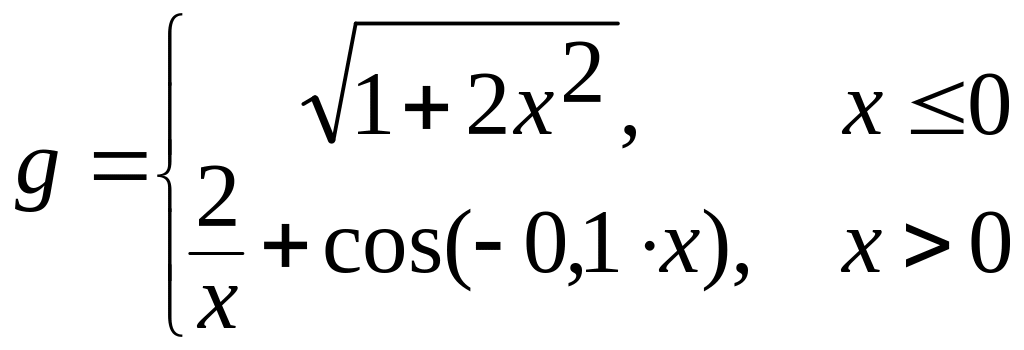 в)
в) 
2. х[-3;0] ![]() и
и ![]()
3. Построить
поверхность
![]() , х,y[-1;1]
, х,y[-1;1]
Вариант 13
х[-2;1,8] а)
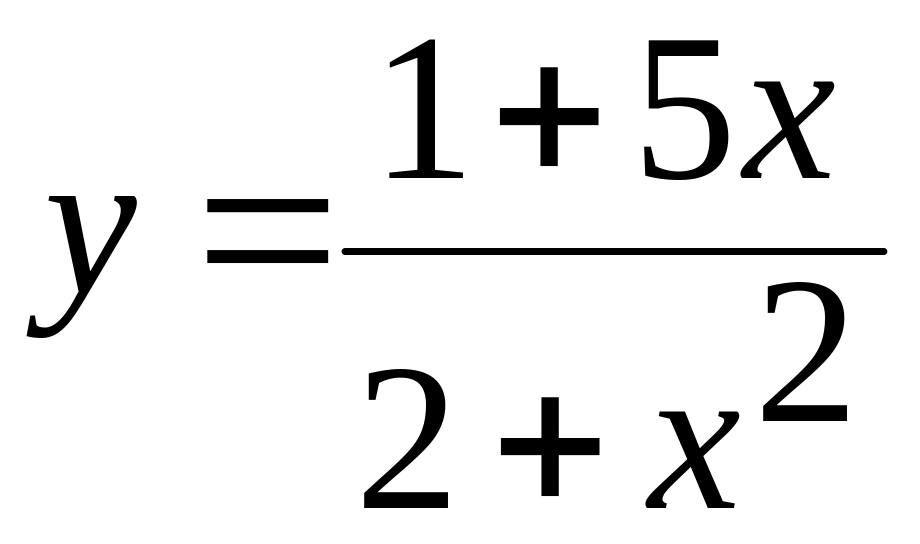
б) 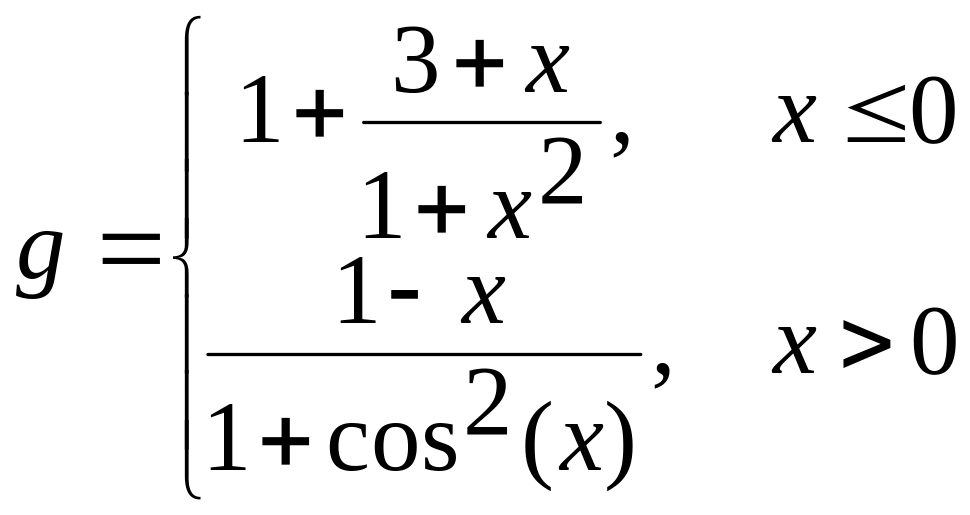 в)
в) 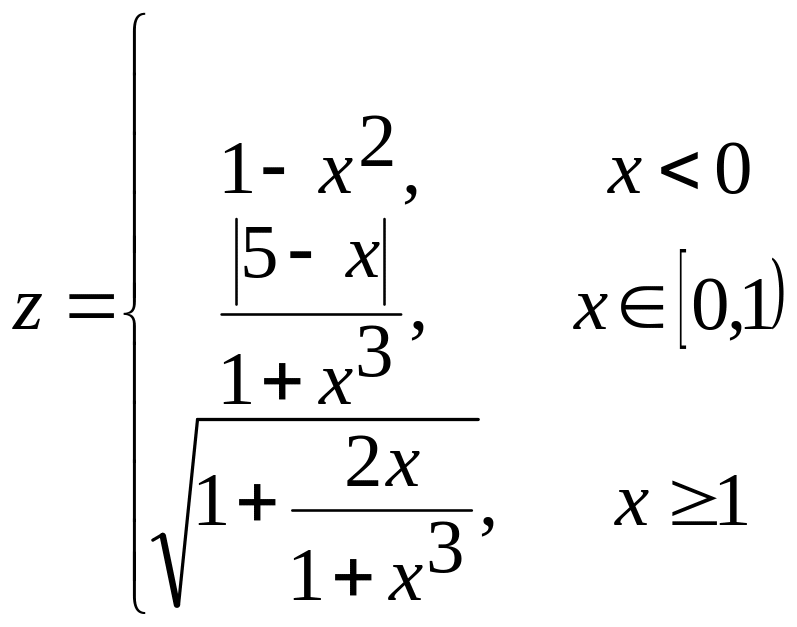
2. х[-3;0] ![]() и
и ![]()
3. Построить
поверхность
![]() при х,y[-1;1]
при х,y[-1;1]
Вариант 14
1. х[-2;1,8] а) 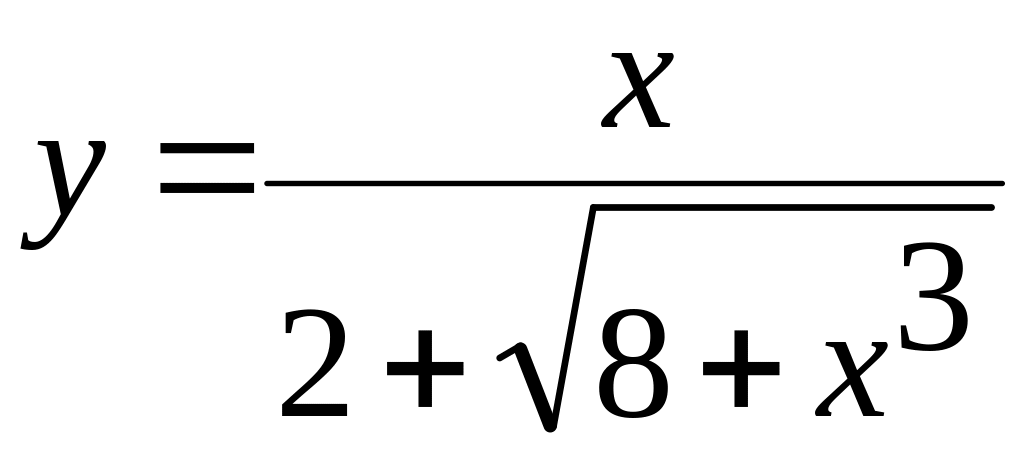
б) 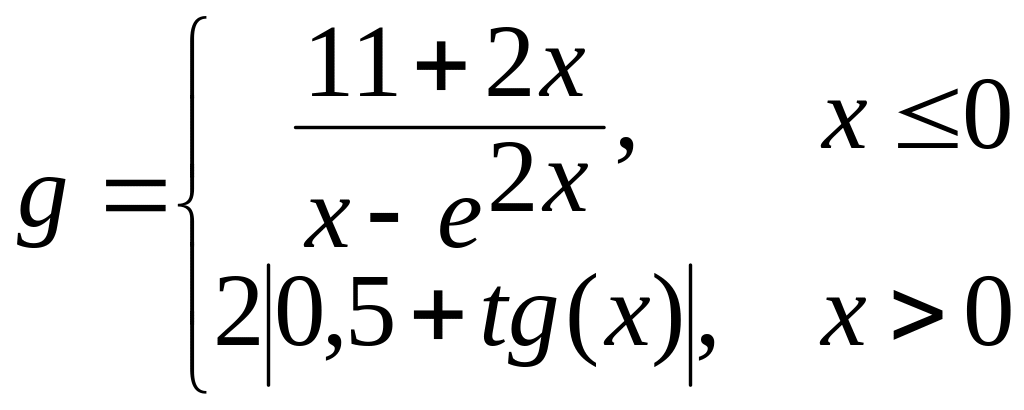 в)
в) 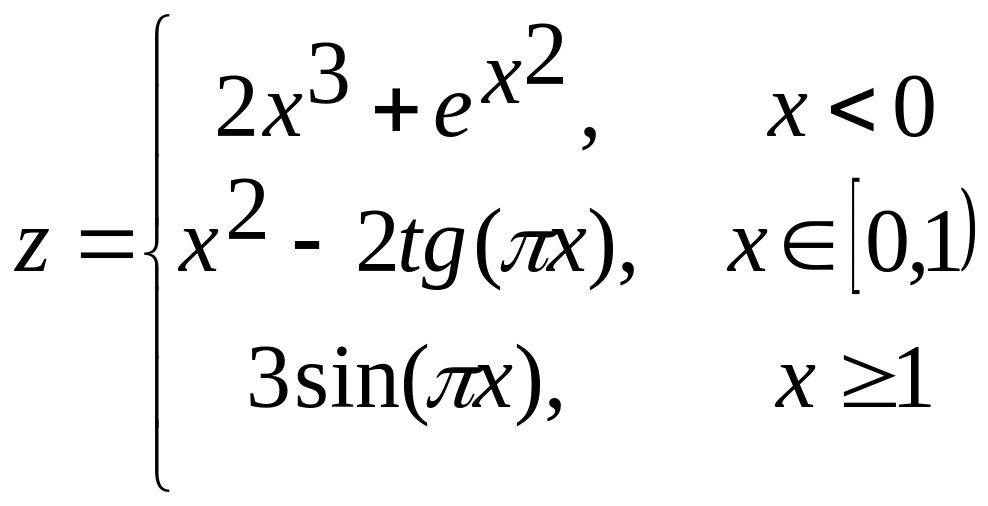
2. х[-3;0] ![]() и
и ![]()
3. Построить
поверхность
![]() при х,y[-1;1]
при х,y[-1;1]
Вариант 15
1. х[-2;1,8] а) ![]()
б)  в)
в) 
2. х[-3;0] ![]() и
и ![]()
3. Построить
поверхность
![]() при х,y[-1;1]
при х,y[-1;1]
Вариант 16
1. х[-1,5;1,8] а)
б) в)
2. х[-2;2] и
Построить поверхность при х,y[-1;1]
Вариант 17
1. х[-2;2] а)
б) в)
2. х[-3;0] и
3. Построить поверхность при х,y[-1;1]
Вариант 18
х[-2;1,8] а)
б) в)
2. х[-2;2] и
3. Построить поверхность при х,y[-1;1]
