4 Проектирование зубчатого механизма

4.1 Синтез планетарного редуктора и определение угловых скоростей звеньев редуктора аналитическим методом

Подбор чисел зубьев колес и планетарного механизма производится на ПК в программе ТММ.ЕХЕ.

Определим исходные данные, необходимые для подбора чисел зубьев.

Зубчатый механизм состоит из последовательно соединенной простой передачи 1-2 и планетарной передачи (колеса 3, 4, 5, 6 и водило Н). Найдем передаточное отношение редуктора в соответсвии с теоремой об общем передаточном отношении.

Передаточное отношение представим в виде:

С другой стороны:

Тогда для планетарной ступени:

Угловая скорость первого колеса редуктора:

Допустимое отклонение передаточного числа .

Используя программу подбора чисел зубьев по заданному и с учетом условий: соосности, соседства и сборки (т.к. устанавливаются 3 блока сателлитов), получаем таблицу 4.1, из которой выбираем вариант №3

96

Таблица 4.1 – Результаты подбора чисел планетарного редктора

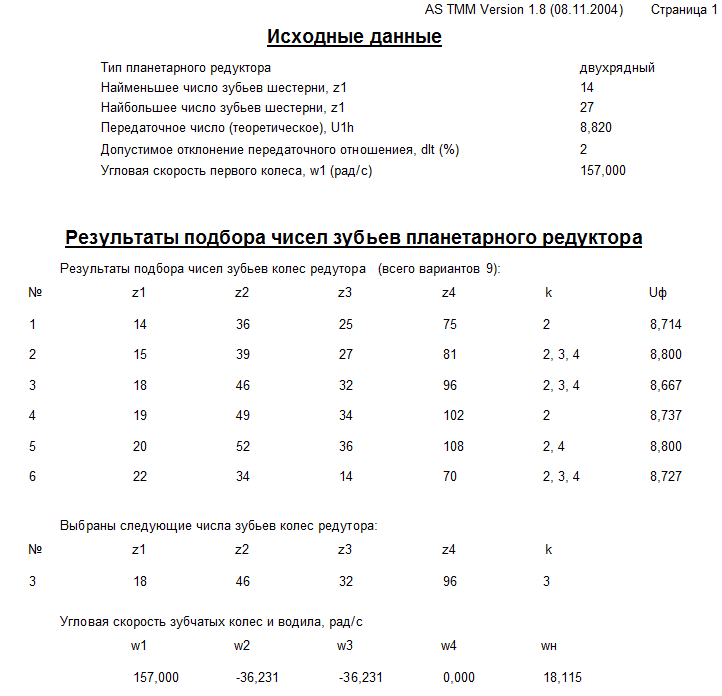
Определим фактическое передаточное отношение:

Для определения применим метод обращения движения механизма: для этого водило Н сделаем неподвижным, а остальным звеньям планетарной передачи добавим угловую скорость ( - ). При этом водила остановиться и планетарный механизм превращается в простой. Получаем обращенный механизм.

Где - передаточное отношение зубчатых передач 3-4 и 5-6 в обращенном механизме.

С другой стороны, можно выразить его следующим образом:

Откуда получим:

Тогда для всего механизма:

Относительная погрешность будет равна:

∆

Определяем угловые скорости звеньев:

Из следует

Из следует

Из ;

=14,4 рад/с

4.2 Построение диаграммы линейных и угловых скоростей зубчатого механизма

Считаем колеса планетарного редуктора нулевыми, тогда радиусы начальных окружностей определяются по формуле:

;

Изобразим схему редуктора в двух проекциях, приняв масштабный коэффициен . Линейная скорость точки А колеса 1 равна:

где

Скорость точки А колеса 1 равна скорости точки А колеса 2, т.е.

;

Зададим значение масштабного коэффициента диаграммы лиейных скоростей

.

Определяем изображение скорости на диаграмме

(Аа) = = = 78,5 мм

Луч - это закон распределения линейных скоростей точек первого класса.

Соединим т.а. с т. - получим закон распределения скоростей точек колес 2,3.

Определим скорость т. В: .

Соединим т. В с т. С – получим закон распределения линейных скоростей точек сателлита, так как колесо 6 – неподвижное, то т.С является мгновенным центром скоростей.

Определим скорость т. D водила и сателлита:

Луч – закон распределения линейных скоростей точек водила Н.

Построим диаграмму для определения угловых скоростей звеньев.

Выберем произвольно полюсное расстояние = 33,3 мм и проведем горизонтальную прямую.

Проводим лучи параллельные законам распределения линейных скоростей из точки Р до пересечения с горизонталью.

Определяем значение масштабного коэффициента диаграммы угловых скоростей:

По диаграмме получим следующие значения угловых скоростей:

Сравним результаты расчета угловых скоростей двумя методами, определив относительную погрешность вычмслений :

∆

∆

∆

∆

∆

Таблица 3.5 – Сравнение данных аналитического и графического методов

Способ определения
Аналитический
Графический
Расхождение, %	0,64	0,32	4,17	2,91