
- •Факультет інженерної механіки
- •1 Структурный и кинематический анализ рычажного механизма
- •Структурный анализ рычажногомеханизма
- •Построение планов механизма, скоростей и ускорений
- •2 Силовое исследование рычажного механизма
- •2.1 Определение масс звеньев, сил тяжести, и центральных моментов инерции
- •2.2 Определение сил реакций в кинематических парах и уравновешивающего момента методом академика Бруевича
- •3 Проэктирование цилиндрической нулевой прямозубой эвольвентной передачи
- •3.1 Геометрический расчет параметров зацепления
- •3.2 Проверка качества зубьев
- •3.3 Вычисление контрольных размеров, проставляемых на чертеже
- •3.4 Построение эвольвентного зацепления
- •4 Проектирование зубчатого механизма
- •4.1 Синтез планетарного редуктора и определение угловых скоростей звеньев редуктора аналитическим методом
- •4.2 Построение диаграммы линейных и угловых скоростей зубчатого механизма
- •5 Проектирование кулачкового механизма
- •5.1 Определение законов движения толкателя и построение их графиков
- •5.2 Построение профилей кулачка
2 Силовое исследование рычажного механизма
2.1 Определение масс звеньев, сил тяжести, и центральных моментов инерции
Используя план
ускорений для положения механизма,
соответствующего угловой координате
кривошипа
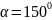 ,
определим ускорения центров тяжести
звеньев:
,
определим ускорения центров тяжести
звеньев:
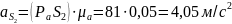
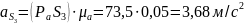
Определим массы звеньевпо формуле:
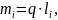
где
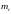 – масса i-го
звена;
– масса i-го
звена;
 – длина i-го
звена;
– длина i-го
звена;
 – масса одного метра звена.
– масса одного метра звена.


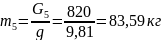
Определим центральные моменты инерции звеньев 2 и 3 по формуле:

где
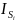 –
центральный момент инерции i-го
звена;
–
центральный момент инерции i-го
звена;
 –
масса i-го
звена;
–
масса i-го
звена;
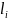 –
длина
–
длина
i-го звена.

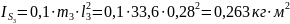
Определим силы
тяжести звеньев 2 и 3
по формуле
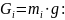

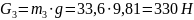
Определим силы инерции звеньев 2,3 и 5:
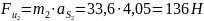


Определим моменты сил инерции звеньев 2 и 3:
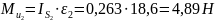

2.2 Определение сил реакций в кинематических парах и уравновешивающего момента методом академика Бруевича
Разбиваем механизм на структурные группы Ассура.
Рассматриваем в равновесии группу Ассура, состоящую из звеньев 4 и 5.
Принимаем
масштабный коэффициент
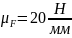 .
.
Строим
многоугольник сил 4 и 5 звеньев и из него
определяем реакции
 ,
,
 :
:
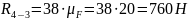
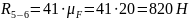
Рассматриваем
в равновесии группу Ассура, состоящую
из звеньев 2 и 3. Для нахождения реакций
 и
и
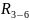 в шарнирах А и С, рассматриваем звенья
2 и 3 в состоянии равновесия. Для удобства
дальнейших расчетов и вычислений делаем
следующие преобразования: двумя силами
заменяем момент сил инерции звена 2
в шарнирах А и С, рассматриваем звенья
2 и 3 в состоянии равновесия. Для удобства
дальнейших расчетов и вычислений делаем
следующие преобразования: двумя силами
заменяем момент сил инерции звена 2
P’2
= P”2
= MU2/lAB
=
 = 17.5 H
= 17.5 H
и звена 3
P’3
= P”3
= MU3/lO2B
=
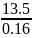 = 84
H
= 84
H
На плане группы изобразим силы реакции:
 – нормальная
составляющая реакции в шарнире А;
– нормальная
составляющая реакции в шарнире А;
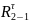 – касательная
составляющая реакции в шарнире А;
– касательная
составляющая реакции в шарнире А;
- полная реакция в шарнире А; = +
 -
нормальная составляющая реакции опоры
4 на звено 3 (в шарнире О2);
-
нормальная составляющая реакции опоры
4 на звено 3 (в шарнире О2);
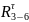 - тангенциальная
составляющая реакции звена 4 на звено
3;
- тангенциальная
составляющая реакции звена 4 на звено
3;
– полная реакция в шарнире. = +
Силы
реакций в шарнирах A
и C
неизвестные по направлению разложим
на 2 составляющие:
 и
и
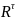 .
.
Составляем условие равновесия для второго звена:

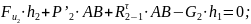
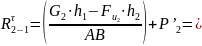

Составляем условие равновесия для третьего звена:
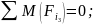
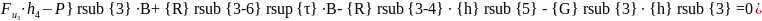
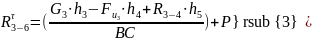

Принимаем
масштабный коэффициент
 .
.
Строим
многоугольник сил второго и третьего
звеньев и из него определяем реакции
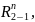
 и
:
и
:

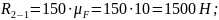
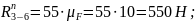

А из условия равновесия звена 2:
 +
+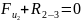
Находим реакцию в шарнире В:
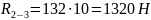

Уравновешивающий
момент
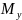 ,
приложенный к кривошипу со стороны
редуктора, определяется из условия
равновесия начального звена 1(которое
изобразим в масштабе
,
приложенный к кривошипу со стороны
редуктора, определяется из условия
равновесия начального звена 1(которое
изобразим в масштабе
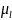 = 0.002 м/мм)
= 0.002 м/мм)
Определим уравновешивающий момент:


 ,
,
где
,

а,
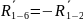
2.3 Проверка уравновешивающего момента методом М.Е. Жуковского
Все активные силы переносим в соответствующие точки повернутого на 90˚ плана скоростей. Уравновешивающий момент заменим парой сил
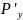 =
=

Составляем уравнение
равновесия плана скоростей (рычага
Жуковского). Берем сумму компонентов
всех сил относительно точки
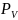 (полюс плана скоростей) и приравниваем
её к нулю:
(полюс плана скоростей) и приравниваем
её к нулю:

·
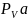 -
-
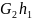 –
–
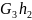 +
+
 +
+
 -
-
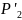 · ab +
· ab +
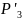 ·
-
·
-
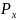 ·
·
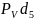 +
+
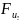 =0
=0

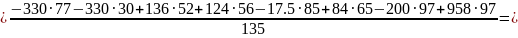
= 415.5 Н
Тогда уравновешеный момент будет:
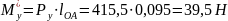
Сравним
результаты расчета
 ,
полученные двумя методами, определив
относительную погрешность вычислений:
,
полученные двумя методами, определив
относительную погрешность вычислений:

Что меньше допустимых 5%.
3 Проэктирование цилиндрической нулевой прямозубой эвольвентной передачи
3.1 Геометрический расчет параметров зацепления
Исходные данные:
 – числа
зубьев всех зубчатых колес;
– числа
зубьев всех зубчатых колес;
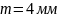 – модуль
всех зубчатых колес;
– модуль
всех зубчатых колес;
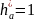 –
коэффициент
высоты головки зуба;
–
коэффициент
высоты головки зуба;
 –
коэффициент
радиального зазора;
–
коэффициент
радиального зазора;
 –
угол профиля
исходного контура.
–
угол профиля
исходного контура.
Коэффициенты смещения находим по таблице 2.1:
 =0.578;
=0.578;
 =1.062;
=1.062;
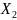 =
-
=1.062 - 0.578 = 0.484.
=
-
=1.062 - 0.578 = 0.484.
Параметры, не изменяющиеся в результате смещения
Шаг по делительной окружности:
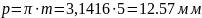
Радиусы делительных окружностей:

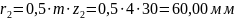
Радиусы основных окружностей:

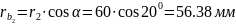
Шаг по основной окружности:

Расчет параметров для нулевого зацепления
Угол зацепления:
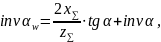
где
 – суммарный коэффициент смещения;
– суммарный коэффициент смещения;
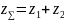 – суммарное число зубьев. Для нулевого
зацепления
– суммарное число зубьев. Для нулевого
зацепления
 тогда:
тогда:
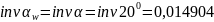

Радиусы начальных окружностей:

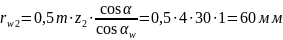
Межосевое расстояние:
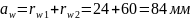
Радиусы окружностей впадин:

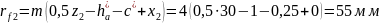
Высота зуба:

Радиусы окружностей вершин:
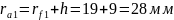
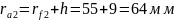
Толщина зубьев по делительным окружностям:


Расчет параметров для неравносмещенного зацепления
Угол зацепления:
где
– суммарный коэффициент смещения;
– суммарное число зубьев;
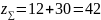 .
Для неравносмещенного зацепления
.
Для неравносмещенного зацепления
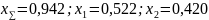 тогда:
тогда:
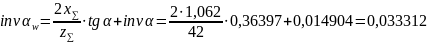
По таблице 2.2 находим:

Радиусы начальных окружностей:


Межосевое расстояние:
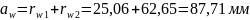
Радиусы окружностей впадин:

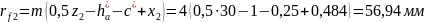
Высота зуба
определяется из условия, что радиальній
зазор равен
 .
Тогда:
.
Тогда:

Радиусы окружностей вершин:
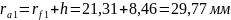

Толщина зубьев по делительной окружности:
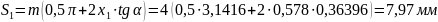

Толщина зубьев по основным окружностям:
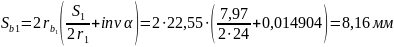
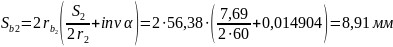
Толщина зубьев по начальным окружностям:

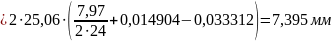
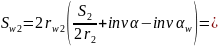
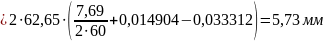
Шаг по начальной окружности:

Проверка:

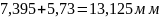
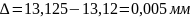
Определим углы профиля на окружностях вершин:
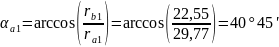

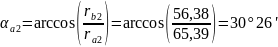
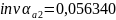
Толщина зубьев по окружностям вершин:
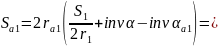

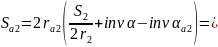

Коэффициент перекрытия:

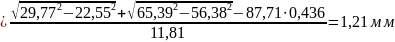
Плавность
передачи обеспечена, т. к.
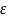 > 1.15
> 1.15
Таблица 3.1 – Расчетные параметры нулевого и неравносмещенногозацеплений

