1 1. Понятие элементарной функции.

Элементарные функции — функции, которые можно получить с помощью конечного числа арифметических действий и композиций из следующих основных элементарных функций:

Каждую элементарную функцию можно задать формулой, то есть набором конечного числа символов, соответствующих используемым операциям. Все элементарные функции непрерывны на своей области определения.

Иногда к основным элементарным функциям относят также гиперболические и обратные гиперболические функции, хотя они могут быть выражены через перечисленные выше основные элементарные функции.

12. Односторонняя непрерьiвность функций, точки разрыва, их классификация.

13. Числовые ряды, необходимые условия сходимости. Свойства сходящихся рядов.

Числовой ряд — это числовая последовательность, рассматриваемая вместе с другой последовательностью, которая называется последовательностью частичных сумм (ряда). Сходимость означает то, что бесконечная последовательность или сумма бесконечного ряда или несобственный интеграл имеют предел.

Понятия имеют смысл для произвольных последовательностей, рядов и интегралов.

1 4. Знакоположительные ряды. остаточные признаки схдимости.

15. Знакопеременные ряды. Абсолютная и условная сходимость. Признак Лейбница,

Числовой ряд, содержащий бесконечное множество положительных и бесконечное множество отрицательных членов, называется знакопеременным. Частным случаем знакопеременного ряда является знакочередующийся ряд, то есть такой ряд, в котором последовательные члены имеют противоположные знаки.

16. Производная, ее геометрический и механический смысл,

Производная. Рассмотрим некоторую функцию y = f ( x ) в двух точках x0 и x0 + : f ( x0 ) и f ( x0 + ). Здесь через обозначено некоторое малое изменение аргумента, называемое приращением аргумента; соответственно разность между двумя значениями функции: f ( x0 + ) - f ( x0 ) называется приращением функции. Производной функции y = f ( x ) в точке x0 называется предел:

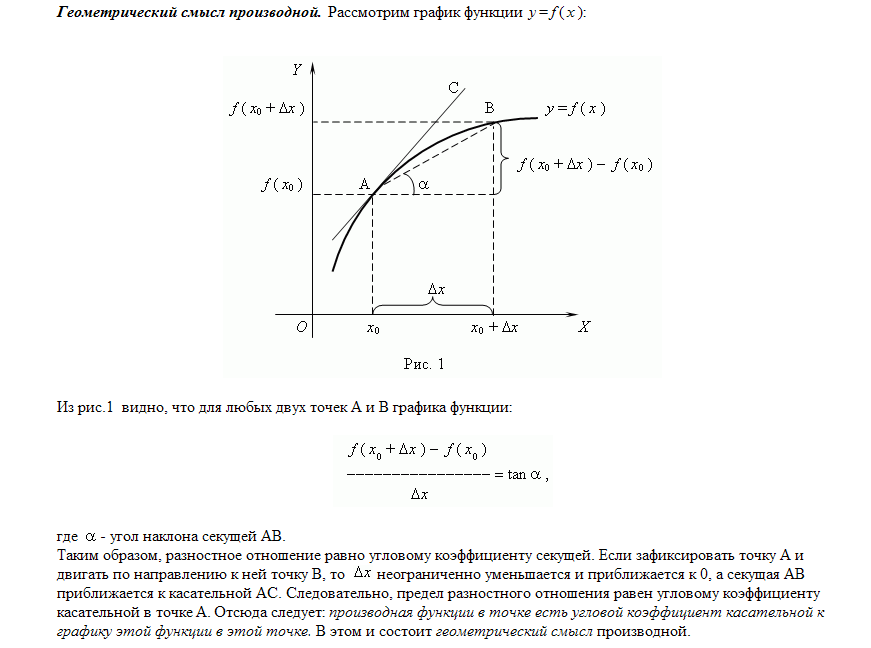
Механический смысл производной. Рассмотрим простейший случай: движение материальной точки вдоль координатной оси, причём закон движения задан: координата x движущейся точки – известная функция x ( t ) времени t. В течение интервала времени от t0 до t0 + точка перемещается на расстояние: x ( t0 + ) - x ( t0 ) = , а её средняя скорость равна: va = / . При 0 значение средней скорости стремится к определённой величине, которая называется мгновенной скоростью v ( t0 ) материальной точки в момент времени t0 . Но по определению производной мы имеем:

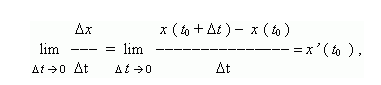
отсюда, v ( t0 ) = x’ ( t0 ) , т.e. скорость – это производная координаты по времени. В этом и состоит механический смысл производной. Аналогично, ускорение – это производная скорости по времени: a = v’ ( t )

1 7. Щифференциал, определение, геометрический смысл.

Дифференциа́л (от лат. differentia — разность, различие) — линейная часть приращения функции

1 8, Арифметические действия над производными,