1)Дайте классификацию видов движения жидкости

Установившееся движение, при котором поперечные сечения потока и средняя скорость в них одинаковы, называется равномерным движением. Примерами равномерного движения могут служить движения воды в трубе постоянного диаметра или в канале с постоянной глубиной и формой поперечного сечения.

Неравномерным называют установившееся движение, при котором поперечное сечение и средняя скорость изменяются по длине потока. Движение воды в трубе переменного диаметра является неравномерным.

Движение потока жидкости может быть напорным или безнапорным. При напорном движении поток ограничен твердыми поверхностями и жидкость полностью заполняет поперечные сечения по его длине. Поток жидкости не имеет свободной поверхности, и движение происходит за счет перепада напоров по длине.

Безнапорным движением называют движение, когда поток частично ограничен твердой поверхностью и имеет свободную поверхность. В большинстве случаев свободная поверхность граничит с атмосферой. Давление на свободную поверхность в этом случае будет равно атмосферному - . Примером может служить движение в трубах с не полностью заполненными поперечными сечениями или поток в канале, реке.

2)Охарактеризуйте физическую сущность коэффициента неравномерности скоростей (корректива скорости) в уравнении Бернулли для потока жидкости.

коэффициент a носит название коэффициента кинетической энергии, корректива скорости, коэффициента Кориолиса. Выясним физический смысл этой величины.

Второй член в уравнении представляет собой кинетическую энергию секундной массы потока, определяемую истинным распределением скоростей в сечении, т.е.  (9.23) Если бы скорости в сечении были бы распределены равномерно, то   (  - средняя скорость потока), и кинетическая энергия потока была бы  (9.24) Разделив (9.23) на (9.24), получим: 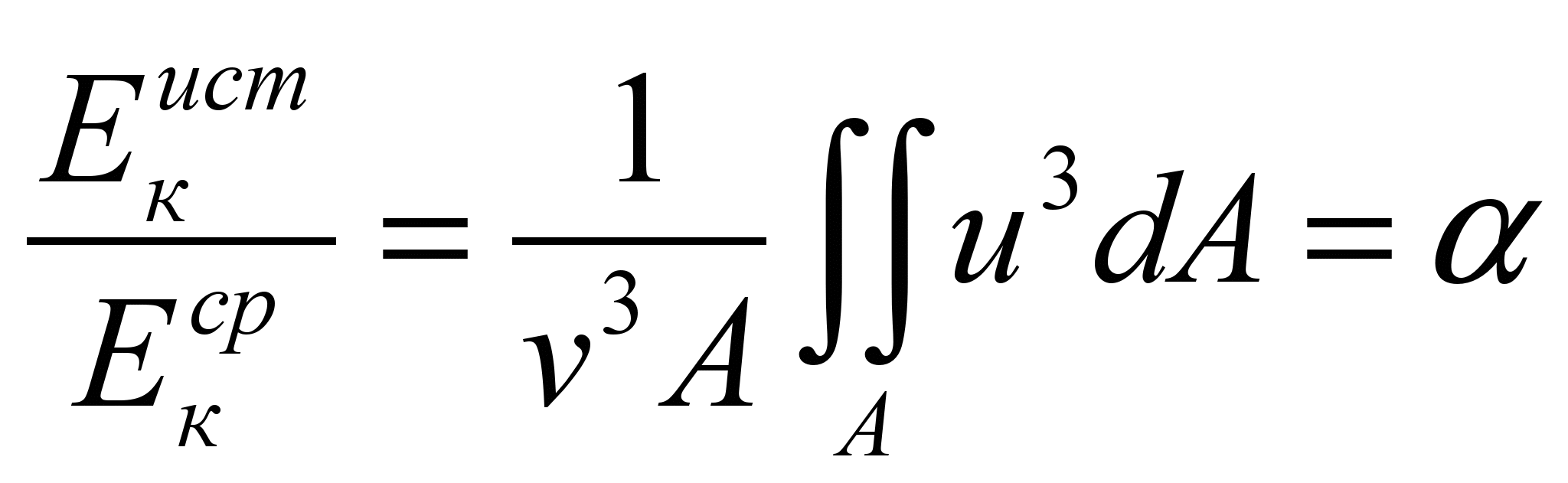  (9.25) Следовательно, коэффициент Кориолиса представляет собой отношение кинетической энергии потока, вычисленной по истинному распределению скоростей, к кинетической энергии, определенной по средней скорости. Для уяснения вопроса рассмотрим гипотетический «поток», состоящий из двух струек, скорости которых  м/с и  м/с и вычислим коэффициент Кориолиса. 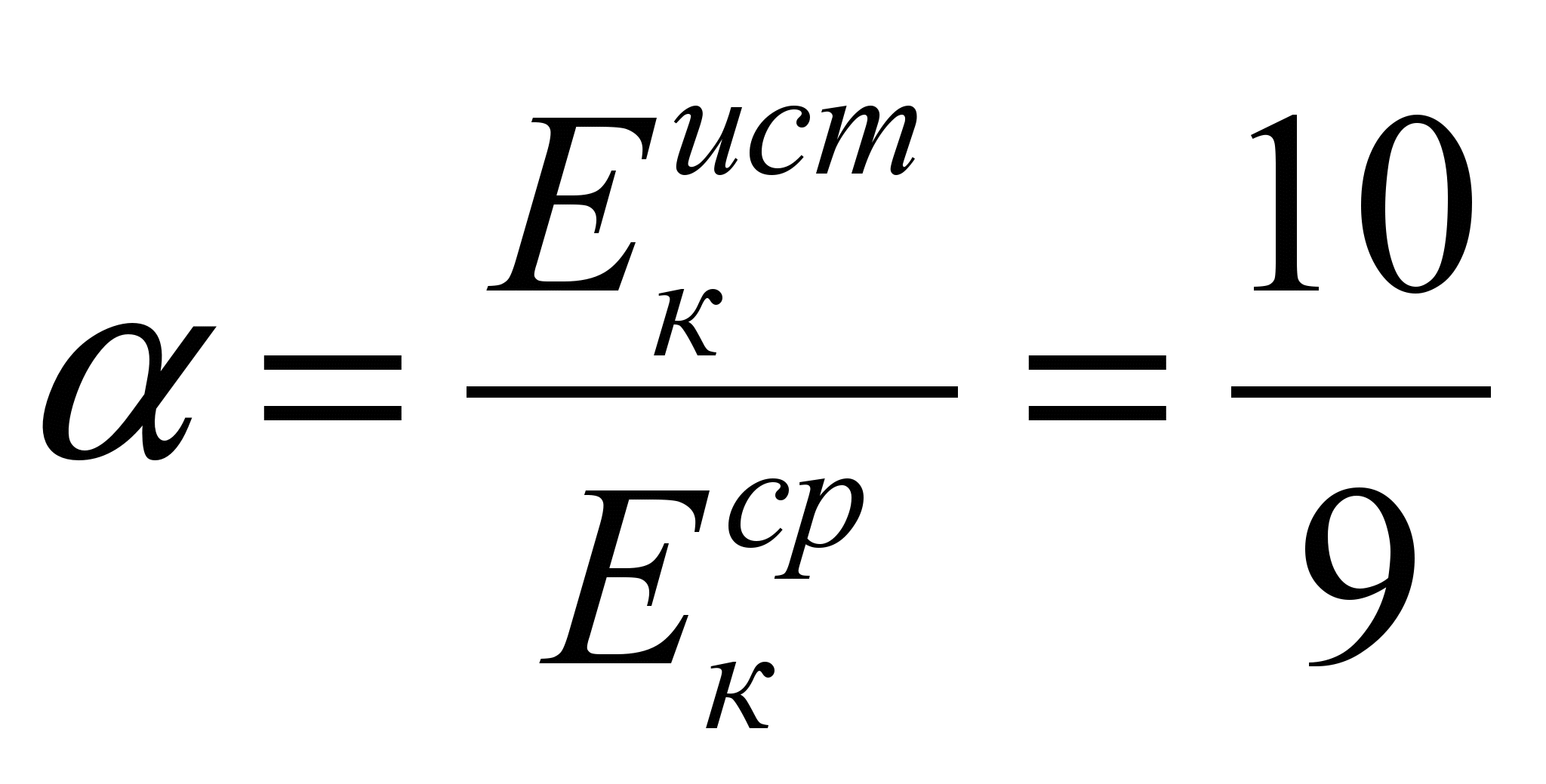Истинная кинетическая энергия (сумма кинетических энергий струек) Средняя скорость  ; и  , т. е.   (истинная кинетическая энергия больше средней). Легко убедится, что чем больше неравномерность распределения скоростей, тем больше коэффициент Кориолиса. Так, если   м/с, а   м/с, то . Очевидно, что минимальное значение   будет при равномерном распределении скоростей. Действительно, пусть   м/с, тогда  и  . Следовательно, можно утверждать, что   корректирует ошибку, возникающую при вычислении кинетической энергии при замене истинного распределения скоростей условным равномерным. Забегая несколько вперед, отметим, что в природе существует два принципиально отличающихся режима течения жидкости: ламинарный и турбулентный. При ламинарном течении в трубах  , при турбулентном  . Это позволяет утверждать, что в турбулентном потоке скорости в поперечном сечении распределены существенно равномерней, чем в ламинарном (эпюра турбулентного потока более «наполненная», ближе к прямоугольной по сравнению с эпюрой ламинарного потока). Подведем некоторые итоги. Использование струйной модели потока и сведение его к одномерному путем введения представления о средней скорости позволяют получить одно из основных уравнений гидродинамики - уравнение Бернулли для потока вязкой жидкости. Принципиально, с помощью этого уравнения можно рассчитать движение жидкости в каналах при установившемся течении и условии, что в выбранных сечениях поток слабодеформированный либо параллельно-струйный. Однако, для полного решения задачи необходимо уметь определять потери напора ( ), возникающие при движении жидкости в каналах.

16 Вычертить универсальный график зависимости коэффициента гидравлических сопротивлений трения от числа Рейнольдса и шероховатости русла.

   Рабочий участок представляет собой длинный горизонтально расположенный   трубопровод   (рис.4.3),   присоединенный   к      питающей установке, описанной в работе №1 (см.рис.1.2). 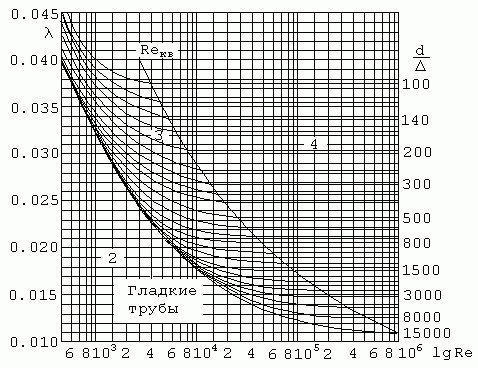  Рис. 4.2. Коэффициент гидравлического трения  для промышленных труб

19 Что выражает собой расходная характеристика трубопровода? По какой формуле определяется?

График уравнения простого трубопровода   носит название его гидравлической харак­ теристики. Вид гидравлической характеристики зави­сит от режима движения жидкости в трубопроводе: при ламинарном движении жидкости гидравлическая характеристика трубопровода - прямая линия, проходящая через начало координат. При турбулентном режиме гидравлическая характеристика - парабола. Определяется по формуле

К=ωС√Rг

где ω – площадь поперечного сечения русла, м

Rг – гидравлический радиус, м

С – коэффициент Шези

27 Виды сжатия струи вытекающей из отверстий

При вытекании жидкости из резервуара через отверстие в тонкой стенке, диаметр которого значительно меньше размеров резервуара, а края отверстия имеют прямоугольную форму, диаметр вытекающей струи будет меньше размеров диаметра отверстия. Это происходит потому, что жидкость, вытекающая из резервуара, попадает в отверстие со всех направлений, а после прохождения отверстия направление движения всех частиц жидкости становится одинаковым. Изменение направления движения частиц жидкости в силу их инерционности мгновенно произойти не может. Поэтому сжатие струи обусловлено необходимостью постепенного изменения направления движения жидкости при прохождении отверстия.  Так как размеры резервуара много больше размеров отверстия, боковые поверхности и свободная поверхность не могут оказывать влияния на направление входа жидкости в отверстие, то в этом случае наблюдается совершенное сжатие струи. Такое сжатие является наибольшим, и оно достигается на расстоянии примерно равном диаметру отверстия. Степень сжатия выражается коэффициентом сжатия :

В том случае, если истечение происходит из резервуара такой формы, что его стенки влияют на траекторию движения частиц при входе в отверстие, наблюдается несовершенное сжатие струи.

Вследствие того, что боковые стенки резервуара перед отверстием формируют направление движения жидкости, струя после отверстия сжимается в меньшей степени, чем при вытекании из практически бесконечного резервуара. По этой причине меняется коэффициент сжатия струи. Формулы для определения этого сжатия для разных жидкостей и разных условий истечения - эмпирические. Например, для круглого центрального отверстия в тонкой торцовой стенке трубы и для маловязких жидкостей коэффициент сжатия  можно находить по следующей эмпирической формуле в долях от коэффициента сжатия  при совершенном сжатии струи

;

где         ;

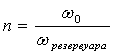где,  в свою очередь,     - площадь отверстия,

 - площадь сечения резервуара (в приведённом примере площадь поперечного сечения трубы

21