Примеры для самостоятельного решения
Задача 8.5
8.5.1.
.
8.5.2.
.
8.5.3*.
.
Линейные однородные уравнения с постоянными коэффициентами
Общий вид линейного дифференциального уравнения порядка n с постоянными коэффициентами
,
(9.1)
где
(i=1,
2, …, n)
– действительные постоянные.
Определение 1. Уравнение
,
(9.2)
полученное
заменой производных
(k=0,
1, …, n)
искомой функции степенями
,
называется характеристическим
уравнением для уравнения (9.1).
Каждому действительному корню λ уравнения (9.2) кратности r соответствует r линейно независимых решений уравнения (9.2):
,
,
…,
,
а
каждой паре комплексных корней
кратности s
соответствует s
пар линейно независимых решений:
,
,
…,
,
,
,
…,
.
Таким
образом, если характеристическое
уравнение имеет k
действительных корней
,
…,
кратностей
,
…,
и l
пар комплексно сопряженных корней
,
,
…,
,
кратностей
,…,
(
),
то общее решение уравнения (9.1) запишется
в виде
,
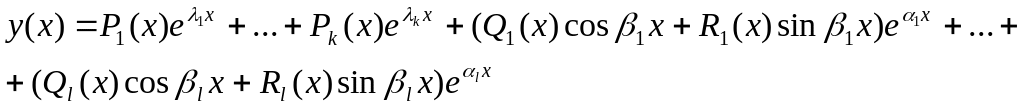(9.3)
где
- произвольный многочлен степени
,
ν=1,
…, k,
а
и
- произвольные многочлены степени
,
μ=1,
…, l.
Решение типовых примеров
Пример 1. Найти общее решение уравнения
.
Решение.
Характеристическое уравнение
имеет корни
.
Следовательно, функции
,
составляют фундаментальную систему
решений, а общее решение имеет вид
.
Пример 2. Найти частное решение уравнения
,
удовлетворяющее начальным условиям y(0)=1, y′(0)=2, y″(0)=3.
Решение.
Характеристическое уравнение
имеет единственный корень λ=1
кратности r=3.
Поэтому фундаментальная система решений
имеет вид
,
,
.
Следовательно,
- общее решение уравнения.
Для определения произвольных постоянных найдем производные
,
и
используем начальные условия. Получаем:
,
,
,
откуда
,
.
Следовательно, искомое частное решение
имеет вид
.
Пример 3. Найти общее решение уравнения
.
Решение.
Характеристическое уравнение
,
или
,
имеет два комплексно сопряженных корня
кратности 2. Следовательно, фундаментальная
система решений имеет вид
,
,
,
.
Отсюда получаем общее решение:
.
Примеры для самостоятельного решения
Задача 9
Найти общие решения дифференциальных уравнений:
9.1.
.
9.2.
.
9.3.
.
9.4.
.
9.5.
.
9.6.
.
9.7.
.
9.8.
.
9.9.
.
9.10.
.
9.11.
.
9.12.
.
9.13.
.
9.14.
.
9.15.
.
9.16.
.
Найти частные решения уравнений по данным начальным условиям:
9.17.
;
.
9.18.
;
,
.
9.19.
;
,
,
.
9.20*.
Найти интегральную кривую дифференциального
уравнения
,
касающуюся в точке О(0,
0) прямой
.
9.21.Найти
интегральную кривую дифференциального
уравнения
,
касающуюся в точке
(0, 2) прямой
.
Линейные неоднородные уравнения. Метод вариации произвольной постоянной
Структура общего решения линейного неоднородного уравнения, то есть уравнения с правой частью:
,
определяется следующей теоремой.
Теорема.
Если
- частное решение неоднородного уравнения,
а
,
,
…,
- фундаментальная система решений
соответствующего однородного
уравнения, то общее решение
линейного неоднородного уравнения
имеет вид
;
иными словами, общее решение неоднородного
уравнения равно сумме любого его частного
решения и общего решения соответствующего
однородного уравнения.
Следовательно, для построения общего решения неоднородного уравнения надо найти его частное решение (предполагая уже известным общее решение соответствующего однородного уравнения).
Рассмотрим два метода отыскания частного решения линейного неоднородного уравнения.
Метод вариации произвольных постоянных. Этот метод применяется для отыскания частного решения линейного неоднородного уравнения n-го порядка как с переменными, так и с постоянными коэффициентами, если известно общее решение соответствующего однородного уравнения.
Метод вариации заключается в следующем. Пусть известна фундаментальная система решений , , …, соответствующего однородного уравнения. Тогда общее решение неоднородного уравнения следует искать в виде
,
где
функции
,
,
…,
определяются из системы уравнений
…………………………………………
,
где f(x) - правая часть данного уравнения.
Для
уравнения второго порядка
соответствующая система имеет вид
.
Решение этой системы находится по формулам
;
,
в силу чего u(x) можно сразу определить по формуле
(здесь
- вронскиан решений
и
).
Примечание.
Отметим, что линейное неоднородное
уравнение второго порядка может быть
проинтегрировано в квадратурах, если
известно одно частное решение
соответствующего однородного
уравнения; общее решение такого уравнения
имеет вид
,
где
определяется через
по формуле
,
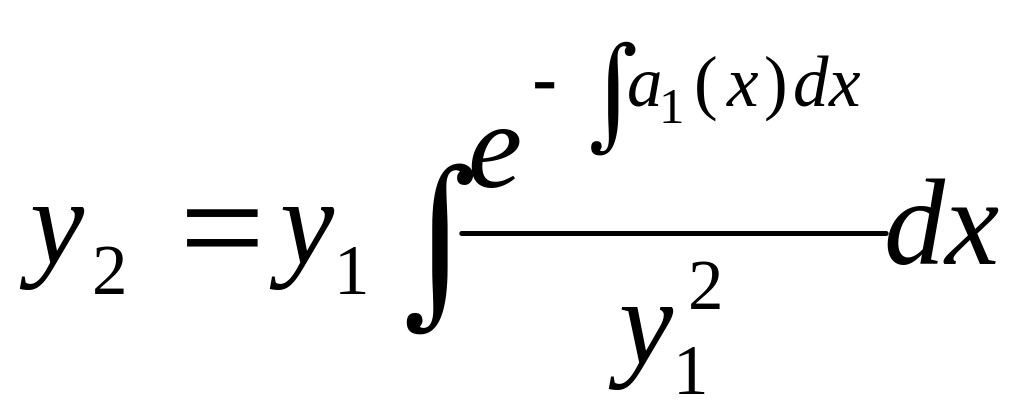а u(x) определяется через и по вышеприведенной формуле.