Перевірка гіпотез про параметри нормального розподілу

Гіпотези такого типу або параметричні гіпотези виникають, наприклад, після застосування критеріїв згоди, тобто, коли встановлено вигляд функції розподілу випадкової величини, але самі параметри, від яких залежить ця функція, - невідомі й потребують уточнення.

Перевіряють параметричні статистичні гіпотези за загальними правилами перевірки гіпотез.

Припустимо, що генеральна сукупність описується випадковою величиною, що має нормальний закон розподілу. Оскільки цей закон розподілу визначається двома параметрами (математичне сподівання) і (середнє квадратичне відхилення),то гіпотези формулюються відносно цих параметрів.

Гіпотези про математичні сподівання

0. Перевірка гіпотези про значення математичного сподівання за відомої дисперсії

Нехай генеральна сукупність розподілена за нормальним законом з невідомим математичним сподіванням , але відомою дисперсією

Варіант І. На основі вибірки потрібно перевірити нульову гіпотезу про рівність математичного сподівання певному числу При цьому передбачаються відомими такі величини:

• вибірку обсягу

• середнє квадратичне відхилення

• гіпотетичне значення математичного сподівання

• рівень значущості

Критерій перевірки цієї гіпотези

має нормальний розподіл з параметрами

Перевірку гіпотези за альтернативної гіпотези здійснюємо за таким правилом:

1. обчислюємо емпіричне значення критерію за формулою:

(3.6)

2. знаходимо за таблицею значень функції Лапласа критичне значення з рівняння:

(3.7)

3. робимо висновок про висунуту гіпотезу:

   • якщо то гіпотезу приймаємо;

   • якщо то гіпотезу відхиляємо на користь альтернативної гіпотези

Перевірку гіпотези за конкуруючої або проводимо за попередньою схемою з такими змінами:

1. замість рівняння (3.7) для знаходження критичного значення використовуємо рівняння:

2. робимо висновки відносно висунутої гіпотези

• якщо то гіпотезу приймаємо;якщо то гіпотезу відхиляємо на користь альтернативної гіпотези

• якщо то гіпотезу приймаємо; якщо то гіпотезу відхиляємо на користь альтернативної гіпотези

Приклад 3.3. Нехай генеральна сукупність розподілена за нормальним законом з відомим середнім квадратичним відхиленням . З цієї генеральної сукупності одержано вибірку обсягу і за нею знайдено вибіркове середнє В задачі потрібно для рівня значущості перевірити нульову гіпотезу за конкуруючої гіпотези :

• 

• 

Розв’язання. Обчислимо емпіричне значення критерію за формулою (3.6):

Розглянемо наведені в умові задачі два випадки:

• для альтернативної гіпотези знаходимо за формулою (3.7) з таблиці додатка 2 :

Отже =1,96. Оскільки то гіпотезу приймаємо;

• для альтернативної гіпотези знаходимо за формулою (22) з таблиці додатка 2

Отже =1б65. Оскільки то гіпотезу відхиляємо на користь альтернативної гіпотези

Варіант ІІ. На основі вибірки потрібно перевірити нульову гіпотезу за умови, що генеральна сукупність розподілена за нормальним законом з невідомими математичним сподіванням і дисперсією

При цьому припускаємо, що відомими є лише наступні величини:

• дані вибірки обсягу

• гіпотетичне значення математичного сподівання

• рівень значущості

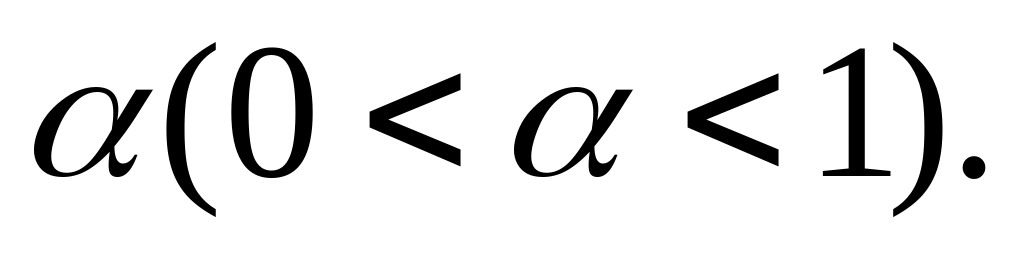
Критерієм перевірки гіпотези в цьому випадку використаємо розподіл Стьюдента з числом ступенів вільності.:

(3.8)

де — вибіркове середнє, а — виправлене вибіркове середнє квадратичне відхилення.

Перевірку гіпотези за конкуруючої гіпотези здійснюємо за таким правилом :

1. обчислюємо емпіричне значення критерію за формулою:

(3.9)

2. з таблиці критичних точок розподілу Стьюдента(див. додаток ) за заданим рівнем значущості і числом ступенів вільності знаходимо критичну точку

3. робимо висновок про висунуту гіпотезу:

• якщо то гіпотезу приймаємо;

• якщо то гіпотезу відхиляємо на користь альтернативної гіпотези

Перевірку гіпотези за конкуруючої або проводимо за попередньою схемою з такими змінами:

1. з таблиці критичних точок розподілу Стьюдента за даним рівнем значущості і число ступенів вільності знаходимо критичну точку

2. робимо висновки відносно висунутої гіпотези

• якщо то гіпотезу приймаємо;якщо то гіпотезу відхиляємо на користь альтернативної гіпотези

• якщо то гіпотезу приймаємо; якщо то гіпотезу відхиляємо на користь альтернативної гіпотези

Приклад 3.4. Для вибірки обсягу значень випадкової величини ,розподіленої за нормальним законом знайдено вибіркове середнє та виправлене середнє квадратичне відхилення В задачі потрібно для рівня значущості перевірити нульову гіпотезу за наявності конкуруючої гіпотези :

Розв’язання. Обчислимо емпіричне значення критерію за формулою (3.9):

Розглянемо наведені в умові задачі два випадки:

• для альтернативної гіпотези за таблицею додатка 2 для числа ступенів вільності і рівня значущості знаходимо Оскільки то гіпотезу приймаємо;

• для альтернативної гіпотези за таблицею додатка 2 для числа ступенів вільності і рівня значущості знаходимо Оскільки то гіпотезу відхиляємо на користь гіпотези