Вопрос 23 Доверительные интервалы

Доверительным называется интервал, который с заданной надежностью   покрывает оцениваемый параметр.

Для оценки математического ожидания   случайной величины  , распределенной по нормальному закону, при известном среднем квадратическом отклонении   служит доверительный интервал

где   - точность оценки,   - объем выборки,   - выборочное среднее,   - аргумент функции Лапласа, при котором 

Вопрос 24 f критерий

С помощью критерия Фишера оценивают качество регрессионной модели в целом и по параметрам.

Для этого выполняется сравнение полученного значения F и табличного F значения. F-критерия Фишера. F фактический определяется из отношения значений факторной и остаточной дисперсий, рассчитанных на одну степень свободы:

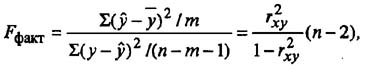
где n - число наблюдений; m - число параметров при факторе х.

F табличный - это максимальное значение критерия под влиянием случайных факторов при текущих степенях свободы и уровне значимости а.

Уровень значимости а - вероятность не принять гипотезу при условии, что она верна. Как правило а принимается равной 0,05 или 0,01.

Если Fтабл > Fфакт то признается статистическая незначимость модели, ненадежность уравнения регрессии.

Вопрос 25 Таблица дисперсионного анализа для линейной регрессии

Оценка значимости уравнения регрессии в целом дается с помощью критерия Фишера. Перед расчетом критерия проводится дисперсионный анализ.

Общая сумма квадратов отклонений у от его среднего значения  раскладывается на объясненную и остаточную регрессии:

  общая          объяснен         остаточная

Если фактор не оказывает влияние на результат, то теоретические значения будут равны среднему.

Р азделив суммы квадратов на соответствующее число степеней свободы, получили дисперсии: Расчетное значение критерия Фишера находится по формуле:   Fтабл. определяется по таблицам распределения Фишера с учетом уровня значимости ά=0,05/0,01/0,1 и числом степеней свободы  ν1 = 1, ν2=n-2. Если Фрасч>Фтабл, уравнение регрессии признается значимым.

Значимость уравнения множественной регрессии оценивается с помощью Ф-критерия Фишера:

M – число параметров при х

Фтабл при α=0,05 V1=m V2=n-m-1

Факт>Фтабл уравнение значимо.

Можно оценить значимость не только уравнения в целом, но и фактора дополнительно включенного в модель. Для этого определяется частный Ф критерий. Оценим значимость влияния х1 как дополнительно включенного фактора:

R2yx1x2xn – коэффициент множественной детерминации для модели с полным набором факторов

R2yx2x3xn  - коэффициент множественной детерминации для модели без учета Х1

Фх1 сравнивается с Фтабл при α=0,05 V1=1 V2=n-m-1

Фх1>Фтабл – дополнительное включение фактора Х1 в модель статистики оправдано и коэффициент чистой регрессии b1 статистики значим.

Фх1<Фтабл – фактор Х1 нецелесообразно включать в модель и коэффициент чистой регрессии статистики незначим

Вопрос 26 Интервалы прогноза по линейному уравнению регрессии

Для каждой точки на линии регрессии можно построить доверит интервалы с

вероятностью р=1-a=0,95, так, что они будут лежать в этих интервалах.

yтеор (хср)=a*+(b*)*хср (2)

Линия регрессии проходит точно через т. (хср;yср).

a*= yср - (b*)*xср (3)

Подставляем в (1): yтеор (хр)= yср + (b*)* (хр- xср).

Цель: выяснить дисперсию этого значения

m2 yтеор (хр)=D yтеор (хр)= D yср + D((b*)*(хр- xср)) - cov(yср +

(b*)* (хр- xср)), где m – среднеквадратич отклонение. Если переменные

неизменны, cov=0.

cov (x;y)=(åi от 1 до n (xi-xср)*(yi-yср))/n.

m2 yтеор (хр)= D yср+(xр-xср)2*Db*= m2 ycр+ (m2 b*)*((xр-xср)2

m2 ycр @ d2yср/n @ S2ост/((n-2)*n) ------- оценка

m2 b*@d2yср*1/(åi от 1 до n (xi-xср)2)@ S2ост/((n-2)*(åi от 1 до n (xi-xср)2)

myтеор (хср)=Корень квадр из (S2ост/(n-2))*корень квадр из

(1/n+(xр-xср)2/(åi от 1 до n (xi-xср)2)).

Для среднеквадратич отклонения точки, лежащей на линии регрессии на оси

абсцисс т.х прогнозное.

txp = (yтеор (хр)-a-b*xp)/ myтеор (хр) – распределена по закону Стьюдента

g(число степеней свободы для парной линейной регрессии)=n-2.

a=0,05, 1-a=0,95