
- •1. Электрический заряд. Взаимодействие электрических зарядов. Закон Кулона. Принцип суперпозиции для сил.
- •2. Электрическое поле. Напряженность электрического поля. Принцип суперпозиции полей.
- •3 Графическое изображение полей. Линии напряжённости электрических полей. Работа сил поля.
- •4 Циркуляция вектора напряженности электростатического поля. Потенциальный характер электростатического поля
- •5. Потенциальная энергия в электростатическом поле. Потенциал. Разность потенциалов,
- •6. Эквипотенциальные поверхности. Сьязь напряженности и потенциала.
- •7 Поток вектора напряжённости. Электростатическая теорема Гаусса.
- •8. Проводник во внешнем электрическим поле. Теоремы Фарадея.
- •9.Диэлектрики.Поляризация диэлектриков.
- •11.Сегнетоэлектрики.Их свойства.
- •12 Электроёмкость. Конденсаторы. Последовательное соединение конденсаторов.
- •13.Электроемкость. Конденсаторы. Параллельное соединение конденсаторов.
- •15.Постоянный электрический ток. Си;.А тока, вектор плотности тока. Уравнение непрерывности. Условие стационарности тока.
- •16. Закон Ома для участка цепи. Электрическое сопротивление. Закон Ома в дифференциальной форме.
- •17 Сторонние силы.Электродвижущая сила источника. Напряжение. Обобщеный закон ома.
- •18 Сторонние силы. Эдс источника. Закон ома для однородного и неоднородного участка цепи.
- •19. Сторонние силы. Электродвижущая сила источника. Закон Ома для замкнутой цепи. Ток короткого замыкания. Режим холостого хода источника.
- •20. Правила Кирхгофа. Последовательное соединение сопротивлений.
- •21.Правила Киртхгофа. Параллельное соединение сопротивлений.
- •22 Работа и мощность тока. Закон Джоуля-Ленца
- •26 Закон Био-Савара-Лапласа. Магнитное поле витка с током.
- •28. Магнитный поток. Теорема Гаусса для магнитного поля в вакууме.
- •29. Циркуляция вектора магнитной индукции. Закон полного тока.
- •31. Сила Ампера. Закон Ампера. Работа силы Ампера.
- •32 Взаимодействие параллельных токов
- •33. Действие магнитного поля на движущийся заряд. Сила Лоренца. Эффект Холла.
- •34. Закон электромагнитной индукции Фарадея. Правило Ленца.
- •35. Явление самоиндукции. Индуктивность
- •36. Взаимная индукция. Трансформатор
- •37 Энергия магнитного поля.
- •38 Электромагнитные волны
- •39. Шкала электромагнитных волн
- •40. Световые волны. Их основные характеристики.
- •41. Интерференция света. Сложение двух когерентных волн.
- •42. Интерференция света. Условия максимума и минимума интерференции.
- •45. Интерцеренционные схемы. Бизеркало Френделя.
- •44. Интерцеренционные схемы. Бипризма Френделя
- •49 Интерференция на клине.
- •51.Дифракция света. Принцип Гюйгенса-Френеля.
- •54. Поляризация света. Виды поляризации
- •55. Свет поляризованный и неполяризованный.
- •46. Интерференционные схемы. Зеркало Ллойда.
- •70 Внешний фотоэффект. Уравнение Эйнштейна.
- •71 Опыт Боте. Фотоны.
- •75. Постулаты Бора. Опыт Франка и Герца.
- •76. Состав и характеристика атомного ядра.
- •77. Масса и энергия связи ядра
- •76.Радиоактивность. Закон радиоактивного распада.
- •79. Ядерные реакции. Ядерный реактор.
- •80.Методы регестрирования эдеиентарных частиц. Камера Вильсона.
- •81. Методы регистрации элементарных частиц. Пузырьковая камера.
- •56.Поляризация света. Закон Брюстера.
- •68. Квантование энергии Формула Планка.
- •52. Дифракция Света. Метод Френеля
- •57. Поляризация света. Оптически активные вещества.
- •58. Дисперсия света. Поглощение света.
- •63. Тепловое излучение. Люминесценция.
- •64. Испускательная и поглощательная способности тела. Абсолютно черное и серое тело. Закон Кирхгофа.
- •82Методы регистрации элементарных частиц. Искровая камера.
- •73. Модель атома Томсона. Опыты по рассеиванию а-частиц. Ядерная модель атома.
- •74.Атом водорода по Бору.
- •10.Теорема Гауса для поля в диэлектрике.
- •14. Энергия и плотность энергии электрического поля.
- •23.Магнитное поле в вакууме. Силовые линии магнитного поля
- •24.Индукция магнитного поля.
- •47.Интерференционные схемы. Билинза Бийе.
- •48.Интерференция в тонких пленках.
- •50.Применение интерференции света. Интерферометр Майкельсона.
7 Поток вектора напряжённости. Электростатическая теорема Гаусса.
Поток вектора напряженности. физическая величина, характеризующая электрическое поле. С помощью этой величины мы сможем рассчитать напряженности электрических полей(Напряженностью электрического поля называют физическую величину, равную отношению силы, с которой поле действует на положительный пробный заряд, помещенный в данную точку пространства, к величине этого заряда: ) |
источниками
которых являются не только точечные
заряды, но и заряды, распределенные
непрерывно по некоторым поверхностям
– плоскости, сфере, цилиндру и т. д.
Элементарным потоком вектора напряженности
через малую площадку называется
произведение модуля вектора
![]() на площадь площадки
на площадь площадки
![]() и косинус угла между вектором
и косинус угла между вектором
и
нормалью к площадке
![]() :
:
![]()
![]() .
(1) Полный поток через поверхность равен
сумме элементарных потоков через все
ее участки:
.
(1) Полный поток через поверхность равен
сумме элементарных потоков через все
ее участки:
![]() .(2)
Чтобы
вычислить значение полного потока,
оказывается полезным ввести еще одно
вспомогательное понятие – телесный
угол.
.(2)
Чтобы
вычислить значение полного потока,
оказывается полезным ввести еще одно
вспомогательное понятие – телесный
угол.
Теорема Гаусса.
Теорема Гаусса — основная теорема электродинамики, которая применяется для вычисления электрических полей. Она выражает связь между потоком напряжённости электрического поля сквозь замкнутую поверхность и зарядом в объёме, ограниченной этой поверхностью.
Поток вектора напряжённости электрического поля через любую, произвольно выбранную замкнутую поверхность пропорционален заключённому внутри этой поверхности электрическому заряду.
![]()
![]() ,
где:
,
где:
![]()
— поток вектора напряженности электрического поля через замкнутую поверхность S. Q — полный заряд, содержащийся в объеме, который ограничивает поверхность
S — электрическая постоянная. Для теоремы Гаусса справедлив принцип суперпозиции, то есть поток вектора напряжённости через поверхность не зависит от распределения заряда внутри поверхности.
8. Проводник во внешнем электрическим поле. Теоремы Фарадея.
Определение: Проводниками называют материалы, имеющие так называемые свободные заряды, которые могут перемещаться в объеме проводника под действием сколь угодно малого внешнего электрического поля.
Типичным
примером проводников являются металлы,
атомы которых при формировании кристалла
решетки отдают в коллективное использование
1-3 -в с внешних оболочек. Эти электроны,
несмотря на то, что находятся в
потенциальной яме объема проводника,
весьма слабо связаны с атомом, то есть
имеют большую подвижность (связь каждого
электрона одновременно принадлежит
всем атомам, что и обеспечивает их
высокую подвижность).
При
помещении проводников во внешнее
электрическое поле, свободные заряды
начинают перемещаться в этом поле, если
в объем проводника был дополнительно
внесен некоторый заряд, то под действием
этого внешнего поля, этот дополнительный
заряд распределиться по поверхности
проводника.
Таким
образом, при электризации проводника
сообщенный ему дополнительный заряд
оказывается, распределен в области
поверхности проводника. Это распределение
заряда будет происходить до тех пор,
пока при распределении заряда потенциал
поля в любой точке проводника не станет
одинаковым.
![]()
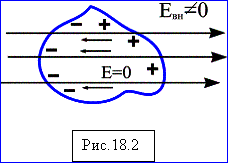
Отметим свойства заряженного проводника во внешнем электрическом поле. 1.Электрический потенциал в любой точке объема равен потенциалу в любой точке поверхности проводника.2Линии электрического поля перпендикулярны поверхности проводника. 3.При помещении заряда проводника во внешнее электрическое поле внутри объема проводника будет наблюдаться движение зарядов до тех пор, пока суммарное поле внутри объема, обусловленное внешним полем, и поле дополнительного заряда не станет равным нулю.
Эквипотенциальные поверхности огибают проводник, помещенный во внешнее электрическое поле, а одна из них, потенциал которой равен потенциалу проводника, пересекает его. Для любого проводника существует только одна поверхность, потенциал которой равен потенциалу поверхности проводника. Теорема Фарадея
Индукция
электромагнитная, возникновение
электродвижущей силы (эдс индукции) в
проводящем контуре, находящемся в
переменном магнитном поле или движущемся
в постоянном магнитном поле. Электрический
ток, вызванный этой эдс, называется
индукционным током. И. э. была открыта
М. Фарадеем в 1831. Согласно закону Фарадея,
эдс индукции Ei в контуре прямо
пропорциональна скорости изменения
магнитного потока (потока вектора
магнитной индукции) Ф через поверхность
S, ограниченную этим контуром:
![]() Здесь
DФ — изменение магнитного потока через
контур за время Dt; коэффициент
пропорциональности k в системе СИ равен
k = 1, а в системе СГС (Гаусса) k = 1/c, c —
скорость света в вакууме. Знак минус
определяет направление индукционного
тока в соответствии с Ленца правилом:
индукционный ток имеет такое направление,
что создаваемый им поток магнитной
индукции через площадь, ограниченную
контуром, стремится препятствовать
тому изменению потока Ф, которое вызывает
появление индукционного тока.
Здесь
DФ — изменение магнитного потока через
контур за время Dt; коэффициент
пропорциональности k в системе СИ равен
k = 1, а в системе СГС (Гаусса) k = 1/c, c —
скорость света в вакууме. Знак минус
определяет направление индукционного
тока в соответствии с Ленца правилом:
индукционный ток имеет такое направление,
что создаваемый им поток магнитной
индукции через площадь, ограниченную
контуром, стремится препятствовать
тому изменению потока Ф, которое вызывает
появление индукционного тока.
В постоянном магнитном поле эдс индукции возникает лишь при таком движении контура, при котором магнитный поток через поверхность, ограниченную контуром, изменяется во времени (т. е. контур при своём движении должен пересекать линии магнитной индукции; при движении вдоль линий поток Ф меняться не будет и эдс не возникнет). В этом случае эдс индукции равна работе магнитной части Лоренца силы по перемещению единичного заряда вдоль замкнутого контура. Если же неподвижный проводник находится в переменном магнитном поле, то эдс индукции равна работе по перемещению единичного заряда вдоль замкнутого контура, совершаемой силами вихревого электрического поля, которое, согласно Максвелла уравнениям, порождается в пространстве при изменении магнитного поля со временем. В системе отсчёта, относительно которой контур покоится, именно это вихревое электрическое поле вызывает движение заряженных частиц, т. е. появление индукционного тока. И. э. лежит в основе работы генераторов электрического тока, в которых механическая энергия преобразуется в электрическую; на этом же явлении основано действие трансформаторов и т. д.
