4 Циркуляция вектора напряженности электростатического поля. Потенциальный характер электростатического поля

Напряженность электрического поля – векторная физическая величина. Направление вектора Е в каждой точке пространства совпадает с направлением силы, действующей на положительный пробный заряд.

Электрическое поле неподвижных и не меняющихся со временем зарядов называется электростатическим (электрическое).

Циркуляцией вектора по замкнутому контуру называют интеграл вида:

, где d – элемент контура (траектории перемещения заряда -замкнутой линии, проведенной в электрическом поле). Силовые поля, которые удовлетворяют этому условию называются потенциальными полями.

Для всех потенциальных полей циркуляция вектора напряженности равна нулю, для вихревых полей (полей с замкнутыми силовыми линиями) такое условие не выполняется. Покажем, что для электростатического поля циркуляция вектора напряженности равна нулю.

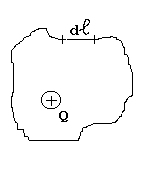
Работа, совершаемая на участке d траектории при перемещении заряда q в поле неподвижного заряда Q, может быть выражена интегралом:

,

отсюда работа по перемещению единичного заряда по замкнутому контуру равна , то есть циркуляции вектора напряженности по замкнутому контуру, но, как было показано ранее, работа по замкнутому контуру равна 0, следовательно и = 0, т.е. электростатическое поле потенциально. Теорема о циркуляции вектора напряженности

электрического поля по замкнутому контуру: = 0

Циркуляция вектора напряженности по любому замкнутому контуру в электростатическом поле равна нулю.

Потенциальный характер электростатического поля

Рис. 1

Потенциальный характер электростатического поля Пусть электрическое поле создано неподвижным точечным зарядом Q, расположенным в начале координат (рис. 1). Будем медленно перемещать в этом поле другой точечный заряд q. При этом на него действует со стороны заряда Q сила F, направленная вдоль той же линии, что и радиус-вектор . Вычислим работу, совершенную силами поля при перемещении заряда (другие силы при этом, конечно, тоже могут действовать, но работа этих сил нас не интересует).

Элементарная работа , где a – угол между силой и направлением перемещения. Из рисунка видно, что , где dr – приращение модуля радиуса-вектора. Таким образом, . Полная работа, совершенная силами поля при перемещении заряда из начальной точки 1 в конечную точку 2, равна:

, где r₁ и r₂ – начальное и конечное расстояния между зарядами Q и q. Из этой формулы видно, что работа не зависит от пути, по которому перемещали заряд q, а зависит только от положения начальной и конечной точек. Таким образом, сила электростатического взаимодействия является потенциальной силой, и для частицы в электростатическом поле можно ввести потенциальную энергию по обычному правилу: А₁₂ = U₁ – U₂ , (3) где

U₁ и U₂ – потенциальная энергия взаимодействия зарядов друг с другом при начальном и конечном взаимном расположении зарядов. Таким образом, потенциальная энергия взаимодействия двух точечных зарядов Q и q, находящихся на расстоянии r друг от друга, равна: . (4) Поле, созданное произвольно распределенным в пространстве неподвижным зарядом тоже, конечно, является потенциальным, так как такое поле является суперпозицией полей, созданных точечными зарядами.