
3 . Параболический тип
Пусть в уравнении Ax2 + Cy2 + Dx + Ey + F = 0 А ≠ 0, С = 0, тогда оно примет вид
Ax2 + Dx + Ey + F = 0.
Можно считать, что A > 0.
Дополнив члены, содержащие x2 и х, до полного квадрата, получим
A(x – x0)2 + Ey = F1.
Если E ≠ 0, то уравнение можно записать в виде y – y0 = a(x – x0)2. Этому уравнению соответствует парабола с осью симметрии, параллельной оси Оу.
Перейдя
к новой системе координат, уравнение
(5) примет вид:
 или
или
 ,
где
,
где
 ,
р – параметр параболы. Координаты
фокуса F будут (0;
,
р – параметр параболы. Координаты
фокуса F будут (0;
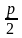 ).
Уравнение директрисы
).
Уравнение директрисы
 .вершина
.вершина
 .
.
Парабола не имеет асимптот. Эксцентриситет параболы равен 1 и не влияет на форму кривой.
Построение параболы.
Построим
часть параболы, расположенной в верхней
полуплоскости, которая выражается
уравнением
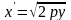 .
При р>0 : если
.
При р>0 : если
 ,
то для у получаем мнимые значения.
Парабола расположена вверх от оси Ох,
т.е. в положительном направлении оси
Оу. у изменяется от 0 до +
,
то для у получаем мнимые значения.
Парабола расположена вверх от оси Ох,
т.е. в положительном направлении оси
Оу. у изменяется от 0 до + ,
х также изменяется от 0 до +
.
Левая часть параболы получается путем
зеркального отображения правой части
относительно Оу.
,
х также изменяется от 0 до +
.
Левая часть параболы получается путем
зеркального отображения правой части
относительно Оу.

Если Е = 0 и F1 > 0, то уравнение A(x – x0)2 = =F1 равносильно уравнениям
 ,
,
 ,
которые определяют пару параллельных
прямых.
,
которые определяют пару параллельных
прямых.
Если Е = 0 и F1 < 0, то получим также уравнение A(x – x0)2 = F1, которому соответствует пустое множество.
Если Е = 0 и F1 = 0, то A(x – x0)2 = 0. Оно определяет пару совпадающих прямых x – x0 = 0.
Если предположить, что А ≠ 0, С = 0, то уравнение (1) будет иметь вид:
Cy2 + Dx + Ey + F = 0.
Аналогично предыдущему можно показать, что при D = 0 это уравнение определяет параболу с осью симметрии, параллельной оси Ох, и может быть приведено к виду x – x0 = а(y – y0)2.
Если D = 0, то уравнение определяет пару параллельных прямых или пустое множество.
Пример: Привести к каноническому виду уравнение 9х2 +4у2 –18х + 24у+9 = 0
А=9, В=0, С=4.
Т.к.
АС =
 = 36 > 0, то уравнение определяет фигуру
эллиптического типа. Дополнив до полных
квадратов, получим
= 36 > 0, то уравнение определяет фигуру
эллиптического типа. Дополнив до полных
квадратов, получим
9(х - 1)2 + 4(у + 3)2 = 36;
 .
.
Эллипс, центр которого в точке О1(1; -3), а полуоси равны 2 и 3.
х = х΄ + 1
у = у΄ - 3
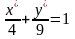
а2 = 4, b2 = 9 и а = 2, b = 3, 2а = 4 – малая ось, 2b = 6 – большая.
Полуфокусное
расстояние: c2
= b2 –
a2 = 9 –
4 = 5; c =
 .
.
Координаты фокусов: F1 = (0; ), F2 = (0;- )
Эксцентриситет
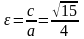 .
.

