Лабораторная работа№1 «Кривые второго порядка»

Определить тип кривой, привести уравнение к каноническому, найти параметры и построить кривую.

1. 9х²+9у²+42х-54у-95=0

2. 3х²+3у²+6х-4у-2=0

3. 4х²+3у²-8х+12у-32=0

4. 2х²+у-8х+5=0

5. 4х²-у+8х+7=0

6. 5у²-10у-х+6=0

7. х²-4х-у+5=0

8. 5х²+у²-20х+2у-4=0

9. 108х²+72у²-108х-48у-397=0

10. 196х²+49у²+56х-98у-143=0

11. 9х²+10у²-54х+60у+81=0

12. 4х²+16у²+4х+64у+1=0

13. 144х²+16у²-72х-128у+121=0

14. у²-6х-2у-2=0

15. 3х²-2у² -6х-8у-17=0

16. 25х²-9у² +50х+18у+241=0

17. 4х²-2у² -4х-12у-25=0

18. х²-6у² +2х+72у-209=0

19. 5х²-2у² +40х+4у+28=0

20. 49х²-196у² +56у+780=0

21. 11х²-4у² +44х=0

22. 9х²-8у² -6х-16у+65=0

23. 4х²+8х+у=0

24. 4х²-4х-32у-63=0

25. 4у²+32у+х+60=0

26. 81х²+64у²-162х+128у-5039=0

27. 256х²+64у²-512х+16у+1=0

28. 4х²+4у²-32х+4у-35=0

29. 2x²-3y²+8x-6y+3=0

30. -16x²+25y²-32x+100y-316=0

31. 4х²+у²-8х+4у=0

32. 2х²+3у²+12х-6у+21=0

33. 4х²-у²+8х-2у+3=0

34. 9х²+16у²+36х-64у-44=0

35. 5х²+3у²+10х+12у+17=0

36. 4х²+9у²-40х+36у+100=0

37. х²-4у²+6х+8у+21=0

38. 4х²-у²-16х-6у+11=0

Лабораторная работа «Кривые второго порядка»

Пусть кривая второго порядка задана общим уравнением Ax²+Bxy+Cy²+Dx+Ey+F=0.

Оно определяет на плоскости хОу кривую эллиптического типа, или гиперболического типа, или параболического типа.

Выясним, какие кривые соответствуют этому уравнению.

Возможны следующие случаи:

1. АС - > 0 – эллиптический тип.

Канонические уравнения фигур эллиптического типа:

- эллипс,

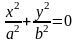- точка,

- пустое множество точек (мнимый эллипс).

2. АС - < 0 – гиперболический тип.

Канонические уравнения фигур гиперболического типа:

- гиперболы,

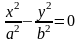- пара пересекающихся прямых.

3. АС - = 0 - параболический тип.

Канонические уравнения фигур параболического типа:

у² = 2рх (х² = 2ру) (р 0) – парабола;

у² = а² (х² = а²) (а 0) – пара параллельных прямых;

у² = 0 (х² = 0) – пара совпадающих прямых;

у² = -а² (х² = -а²) (а 0) – пустое множество точек.

Дальнейшие преобразования рассмотрим для каждого типа кривых.

Пусть в уравнении Ax² + Bxy + Cy² + Dx + Ey + F = 0 отсутствует член с произведением xy (В = 0), т.е. уравнение имеет вид:

Ax² + Cy² + Dx + Ey + F = 0 (1)

1. Эллиптический тип.

Преобразуем уравнение Ax² + Cy² + Dx + Ey + F = 0 к одному из канонических уравнений.

Дополним до полного квадрата члены, содержащие х² и х, а также y² и y. После этого уравнение можно будет записать в виде A(x – x₀)² + C(y – y₀)² = F₁ (2)

Если F₁ > 0, то уравнение (2) приводится к виду , (3)

где , .

Перейдем к новой системе координат. Связь между старыми и новыми координатами некоторой точки плоскости определяется следующими формулами:

, ,

, .

При переходе основной системы координат хОу к новой х΄О₁у΄ направление осей прежнее, за новое начало координат принята точка О₁( ; ).

Уравнение (3) примет вид:

Это уравнение определяет эллипс. Вершинами эллипса будут точки А₁(а; 0), А₂(-а; 0), В₁(0; b), B₂(0, -b). Отрезки А₁А₂ = 2а; В₁B₂ = 2b соответственно большая и малая оси эллипса, а их половины а и b – большая и малая полуоси. Для эллипса, фокусы которого лежат на оси Ox, a > b; полуфокусное расстояние . Координаты фокусов F₁ и F₂ будут (с; 0) и (-с; 0). А для эллипса, фокусы которого лежат на оси Oу, b > a; полуфокусное расстояние . 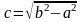Координаты фокусов F₁ и F₂ будут (0; c) и (0; -c).

Осями симметрии эллипса служат оси координат. Оси симметрии эллипса называются его осями. Точка О₁ пересечения осей эллипса; являющаяся центром его симметрии, называется центром эллипса.

Эксцентриситетом эллипса называется отношение расстояния между фокусами к длине большой оси. Обозначив эксцентриситет через 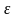, получим . Эксцентриситет характеризует форму эллипса. Эксцентриситет любого эллипса содержится в промежутке [0; 1].