Раздел 7. Элементы математической статистики. Статистическое распределение выборки Вопросы для обсуждения:

1. Случайная величина, значение случайной величины, вариационный ряд; характеристики выборки.

2. Первичная обработка опытных данных при изучении случайной величины.

3. Наглядное представление статистической информации (полигон частот, гистограмма).

Задания и вопросы для подготовки к занятию

1. Пусть М – число выпадений «орла» при десяти подбрасываниях монеты. Подбросьте монету 10 раз и запишите результат. Сравните с результатами ваших однокурсников. Какие значения может принимать величина М? Какие значения получались чаще?

2. Запишите число дня рождения ваших студентов вашей группы. В какой половине месяца в вашей группе больше именинников? Есть ли такое число месяца, в которое в вашей группе нет ни одного именинника? Можно ли сделать вывод, что в день с таким числом не рождаются люди?

Общие теоретические сведения Случайные величины

Случайной называется величина, которая в результате опыта принимает то или иное заранее неизвестное числовое значение. Каждой случайной величине Х соответствует некоторое множество чисел. Это – множество значений, которые может принимать величина Х.

Дискретная случайная величина – случайная величина Х, принимающая отдельные значения х_i с вероятностями p_i. Причем, если x₁, x₂, … – возможные значения величины Х, а р₁, р₂, … – их вероятности, то р₁ + р₂ + … = 1. Примером случайной величины может служить количество выпавших очков при подбрасывании игрального кубика:

x₁ = 1, x₂ = 2, …, x₆ = 6, р₁ = р₂ = … = р₆ = .

Непрерывная случайная величина – случайная величина, которая принимает любые значения из некоторого интервала на множестве действительных чисел. Например, температура воздуха в определённый день, вес ребёнка в каком-либо возрасте, и т.д.

Числовые характеристики случайных величин

Математическое ожидание М(Х) и дисперсия D(X) – наиболее часто применяемые характеристики случайной величины. Они характеризуют наиболее важные черты распределения: его положение и степень разбросанности.

Математическое ожидание дискретной случайной величины Х – сумма всех произведений её возможных значений на их вероятности:

. (7.1)

Если все значения случайной величины равновероятны, то математическое ожидание – среднее арифметическое значений.

Дисперсией дискретной случайной величины Х называется математическое ожидание квадрата отклонения случайной величины от ее математического ожидания:

. (7.2)

Дисперсию можно вычислять по формуле: разности между математическим ожиданием квадрата случайной величины Х и квадратом ее математического ожидания:

. (7.3)

Пример 1. В качестве случайной величины Х возьмем число очков, выпавших на одной игральной кости. Вероятность выпадения каждой грани одинаковы и равны . Поэтому

.

xi	1	2	3	4	5	6
xi – М(Х)	– 2,5	– 1,5	– 0,5	0,5	1,5	3,5
Вероятность

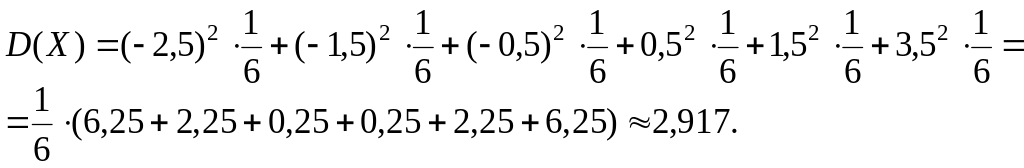
У дисперсии есть недостаток: дисперсия измеряется не в тех единицах, что сама случайная величина, а в квадратных. Но не для всех единиц измерения существуют квадратные (сантиметр – квадратный сантиметр, метр – квадратные метр; килограмм – ?, минута – ?). По этой причине вместо дисперсии часто используется мера рассеивания, которая называется средним квадратичным или стандартным отклонением^ (и равна арифметическому квадратному корню из дисперсии.

. (7.4)

В рассмотренном примере с бросанием кости .