ПЕТЕРБУРГСКИЙ ГОСУДАРСВЕННЫЙ УНИВЕРСИТЕТ

ПУТЕЙ СООБЩЕНИЯ

Кафедра «Электротехника»

РАСЧЁТ И АНАЛИЗ РАБОТЫ ЦЕПИ ПОСТОЯННОГО ТОКА

Выполнил:

студент группы ПТМ-411

Степанов А. О.

Дата выполнения: 19. 10. 2006г.

2006

Вариант 19

Схема электрической цепи:

А I₃ R₃ В

I ₁ I₂ I₄ I₆ I₇

R₁ R₂ R₄ R₆ R₇

Е₁ Е₂ U_AC

U₆₇

R₅

Д I₅ С

Дано: Е₁=100В; Е₂=95В; R₁=0,5 Ом; R₂=0,5 Ом;R₃=1 Ом;R₄=5Ом;R₅=0,5 Ом;R₆=R₇=8 Ом. определить напряжение между узлами «А» и «Д».

Вычислить:

1. Вычислить все токи и определить их направления. Обозначить направления токов на исходной схеме.

2. Вычислить напряжение между узлами «А» и «Д» схемы.

3. Установить режим работы источника.

4. Вычислить мощности развиваемые источниками э. д. с. и потребляемые приёмниками ( Р₃, Р₄, Р₅, Р₆, Р₇).

5. Проверить баланс мощностей цепи.

6. Вывод.

7. Сводная таблица.

1. Эквивалентное преобразование схемы.

Сопротивления R₆ и R₇ соединены параллельно. Заменим их одним эквивалентным сопротивлением R₆₇. Его величина:

; Ом

Получим схему: A R₃ B

R₁ R₂ R₆₇

R₄

E₁ E₂

R₅

C

Д

Сопротивления R₆₇ и R₃ соединены последовательно, значит их можно заменить одним эквивалентным сопротивлением, которое будет равно их сумме:

R₃₆₇=R₃+R₆₇=1+4=5 Ом

Полученная схема будет иметь вид:

A

R₁ R₂ R₄ R₃₆₇

E₁ E₂

C

Д R₅

Сопротивления R₃₆₇ и R₄ соединены параллельно, значит их общая проводимость будет равна сумме их проводимостей. Из этого условия найдём их Эквивалентное сопротивление и обозначим его R_AC (участок цепи между узлами А и С).

Ом

Полученная схема будет иметь вид:

A

R₁ R₂ R_AC

Е₁ Е₂

R₅

Д

Сопротивления R_АС и R₅ соединены последовательно и их общее сопротивление R_Э (эквивалентное) равно сумме их сопротивлений:

R_Э=R₅+R_АС=0,5+2,5=3 Ом

Вид преобразованной схемы:

А

R₁ R₁

R_Э

E₁ E₂

Д

2 . Метод уравнений Кирхгоффа.

А

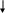
I ₁ I₂ I₅

R₁

I R₂ R_Э

Е₁ Е₂

II

Д

Этот метод основывается на использовании первого и второго законов Киргоффа.

Первый закон Кирхгоффа: алгебраическая сумма токов у проводниках сходящихся к узлу электрической цепи равна нулю.

Второй закон Кирхгоффа: в любом замкнутом контуре электрической цепи алгебраическая сумма Э. Д. С. Равна алгебраической сумме падений напряжения на всех участках контура.

m - число источников Э. Д. С.

i – число участков контура

Произвольно зададимся направлениями токов в ветвях.

Число уравнений должно быть равным числу неизвестных токов, т.е.- три.

По первому закону Кирхгоффа составим число уравнений на одно меньше, чем узлов в схеме т. е. – одно. Рассмотрим узел А:

I₁+I₂-I₅=0

Оставшиеся два уравнения составим по второму закону Кирхгоффа. Для этого необходимо задаться направлениями обхода контуров.

Контур I:

E₁=I₁∙R₁+I₅∙R_Э

Контур II:

E₂=I₂∙R₂+I₅∙R_Э

I ₁+I₂-I₅=0 I₁+I₂-I₅=0 I₁+I₂-I₅=0

E ₁=I₁∙R₁+I₅∙R_Э 100=I₁∙0,5+I₅∙3 I₁∙0,5+I₂∙0+I₅∙3=100

E₂=I₂∙R₂+I₅∙R_Э 95=I₂∙0,5+I₅∙3 I₁∙0+I₂∙0,5+I₅∙3=95

Систему решаем с помощью определителей в программе Excel.

Главная матрица:

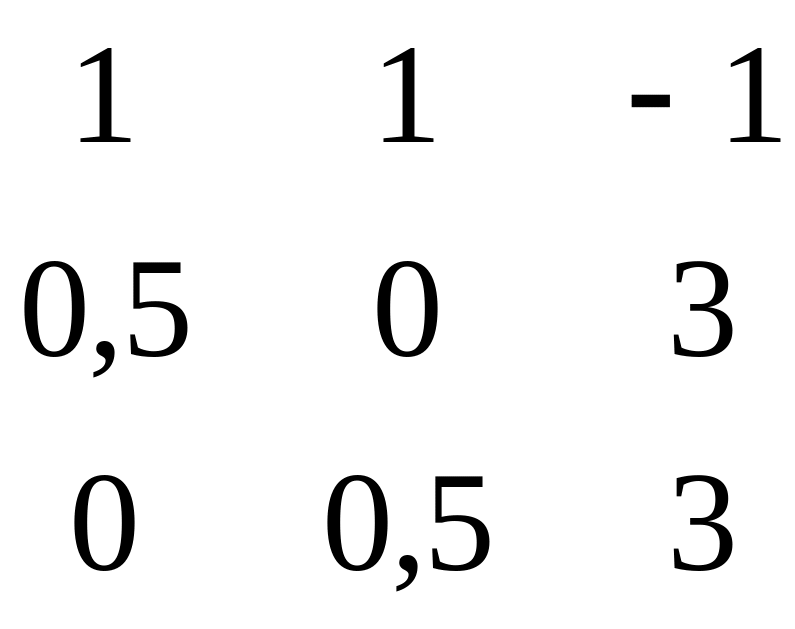
Главный определитель: ∆=-3,25

Первая матрица:

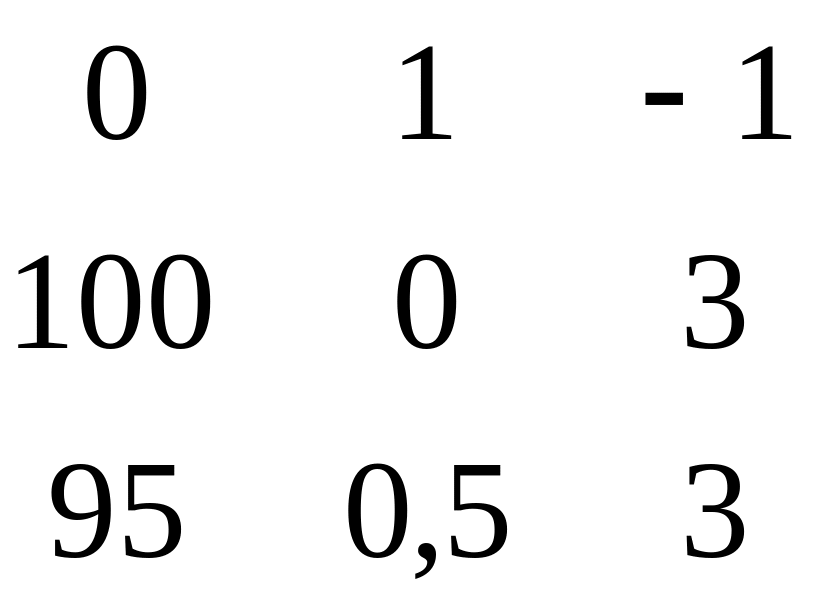
Первый определитель: ∆₁=-65

Вторая матрица:

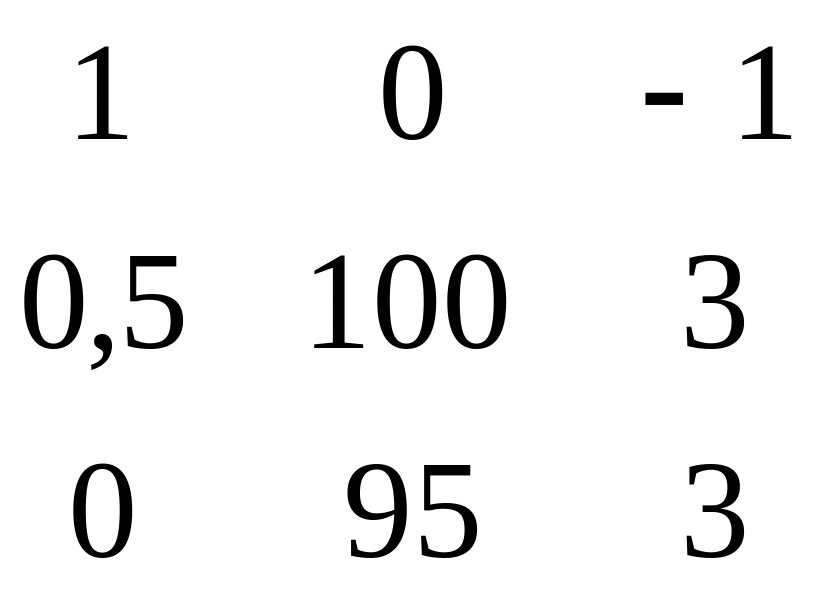
Второй определитель: ∆₂=-32,5

Третья матрица:

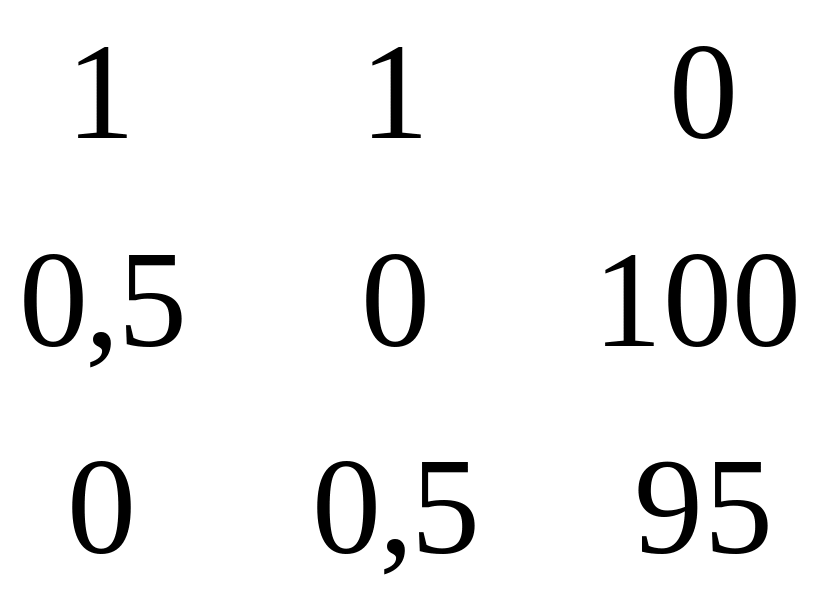
Третьий определитель: ∆₃=-97,5

При решении получаем:

;

;

.

Проверка по первому закону Кирхгоффа (узел А):

20+10-30=0 – выполняется, значит токи найдены верно. Так как значения полученных токов положительны, то выбранные направления верны.

3. Метод узловых потенциалов.

А

I₁ I₂ I₅

R₁ R₂ R_Э

Е₁ Е₂

U_AД

Д

Узел А примем за опорный, т. е. считаем, что потенциал в этом узле равен нулю.

Напряжение между узлом А и любым другим узлом называется узловым напряжением.

Для каждой активной ветви составим уравнения по второму закону Кирхгоффа. При этом узловое напряжение примем равным падению напряжения на участке. Направление обхода примем по часовой стрелке.

А

R

Е U_АД

Д

E₁=I₁∙R₁+U_АД

E₂=I₂∙R₂+U_АД

U_АД= I₅∙R_Э

Из этих уравнений получаем:

, где - проводимость ветви.

, где - проводимость ветви.

, где - проводимость ветви.

В соответствии с первым законом Кирхгоффа для узла А можно записать:

I₁+I₂-I₅=0 или

+ - =0

Раскроем скобки и преобразуем:

E₁∙g₁-U_АД∙g₁+E₂∙g₂-U_АД∙g₂-U_АД∙g_Э=0

U_АД∙(g₁+g₂+g_Э)=E₁∙g₁+E₂∙g₂

Проводимости:

;

Тогда напряжение между узлами А и Д:

Используя полученные выше выражения для токов, получим:

I₁=(E₁-U_AД)∙g₁=(100-90) 2=20A

I₂=(E₂-U_AД)∙g₂=(95-90) 2=10A

I₅=U_АД∙g_Э=90∙0,333=30А

Возвращаемся к исходной схеме. А

R₁ R₂ R₃₆₇

R₄

E₁ E₂ U_AC

U_АД

R₅

Д С

Межузловое напряжение между узлами А и С:

U_AC=I₅∙R_AC=30∙2,5=75B

По закону Ома:

A R₃ B

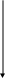
R₁ R₂ R₄ R₆ R₇

Е₁ Е₂ U_AC

U_АД U₆₇

R₅

Д C

Межузловое напряжение между узлами В и С:

U₆₇=I₃∙R₆₇=15∙4=60B

По закону Ома:

Режим работы источников. Так как направления э. д. с. обоих источников и направления токов, текущих через них совпадают то оба источника работают в режиме генератора.

Определение мощностей развиваемых источниками:

P_U1=E₁∙I₁=100∙20=2000Вт

P_U2=E₂∙I₂=95∙10=950Вт

Определение мощностей потребляемых:

P₁=I₁²∙R₁=20²∙0,5=200Вт

P₂=I₂²∙R₂=10²∙0,5=50Вт

P₃=I₃²∙R₃=15²∙1=225Вт

P₄=I₄²∙R₄=15²∙5=1125Вт

P₅=I₅²∙R₅=30²∙0,5=450Вт

P₆=Р₇=I₆²∙R₆=7,5²∙8=450Вт

Баланс мощностей:

P_U1+P_U2=P₁+P₂+P₃+P₄+P₅+P₆+P₇

В правой части стоит арифметическая сумма мощностей потребляемых источниками, а в левой части стоит алгебраическая сумма мощностей выделяемых источниками. Если в результате расчётов получится что ток в какой либо активной ветви и Э. Д. С. По направлению не совпадают, то в этой ветви содержится не источник, а потребитель электрической энергии, например заряжающийся аккумулятор, и в левой части эту мощность надо брать со знаком “-“.

2000+950=200+50+225+1125+450+450+450

2950=2950

Баланс мощностей сходится.