ФЕДЕРАЛЬНОЕ АГЕНТСТВО ПО ОБРАЗОВАНИЮ

ГОУ ВПО «НОВОСИБИРСКИЙ ГОСУДАРСТВЕННЫЙ ПЕДАГОГИЧЕСКИЙ УНИВЕРСИТЕТ»

А. В. Кириллов сопротивление материалов. Решение задач

Утверждено Редакционно-издательским советом НГПУ

в качестве учебного пособия

Новосибирск 2007

УДК 539.2/.6(075.8) Печатается по решению

ББК 30.12 я 73-4 Редакционно-издательского совета НГПУ

К-431

Научный редактор –

кандидат технических наук, профессор,

зав. кафедрой машиноведения НГПУ

В.М. Потапов

Рецензенты:

доктор технических наук, профессор

кафедры механики НТИ МГУДТ

А.М. Красюк;

доктор технических наук, профессор,

зав. кафедрой «Материаловедение в машиностроении» НГТУ

А.А. Батаев

К-431 Кириллов, А.В. Сопротивление материалов. Решение задач: учебное пособие /А. В. Кириллов. – Новосибирск: Изд. НГПУ, 2007. – 138 с.

Настоящая работа является руководством к решению студентами практических задач по курсу «Сопротивление материалов». Основное содержание пособия – примеры решения типовых задач, снабженные необходимыми теоретическими сведениями, варианты домашних заданий и контрольных работ, а также вопросы для самопроверки после каждого раздела.

Пособие предназначено для студентов, обучающихся по специальностям «Профессиональное обучение» (машиностроение и технологическое оборудование; автомобили и автомобильное хозяйство), «Технология и предпринимательство» и «Сервис».

УДК 539.2/.6(075.8)

ББК 30.12 я 73-4

© Кириллов А.В., 2007

© ГОУ ВПО «Новосибирский государственный педагогический университет», 2007

ВВЕДЕНИЕ

Предлагаемое учебное пособие написано в соответствии с Государственными образовательными стандартами по специальностям 030500.8 «Профессиональное обучение (машиностроение и технологическое оборудование)» (специализация 030501.08 «Технология и оборудование машиностроения»); 050501.15 «Профессиональное обучение (автомобили и автомобильное хозяйство)»; 030600 «Технология и предпринимательство» (специализации 030619 «Конструирование и моделирование одежды» и 030601 «Техника и техническое творчество»); 230700 «Сервис» (специализации 230712 «Автосервис» и 230708 «Сервис бытовых машин и приборов»).

Основная цель пособия – изучение и закрепление теоретического материала по дисциплине «Сопротивление материалов» в ходе выполнения студентами домашних заданий и контрольных работ, приобретение навыков при решении практических задач. В процессе усвоения курса и приобретения определенных навыков, а также выполнения домашних заданий, контрольных и лабораторных работ студенты должны получить представление о методах, применяемых при расчетах на прочность и жесткость при различных видах деформаций как для статически определимых, так и статически неопределимых систем.

Порядок изложения решения рассмотренных типовых задач соответствует расположению учебного материала в общем курсе «Сопротивление материалов», а их содержание и направленность – практическому усвоению и закреплению теоретических знаний при изучении этой дисциплины.

Пособие адресовано студентам факультета «Технологии и предпринимательства».

1. РАСЧЕТЫ НА ПРОЧНОСТЬ И ЖЕСТКОСТЬ ПРИ ОСЕВОМ РАСТЯЖЕНИИ-СЖАТИИ

Построение эпюр продольных сил. Растяжение-сжатие – простейший вид деформаций, при котором внешние силы приложены вдоль продольной оси бруса, а в поперечном сечении его возникает только продольная (нормальная) сила.

Расчеты на прочность и жесткость при растяжении-сжатии начинаются с построения эпюры продольной силы с помощью универсального метода сечений, применяемого для построении эпюр внутренних силовых факторов [1 – 7, 9, 11]. Сущность этого метода заключается в следующем:

• рассекаем элемент конструкции плоскостью, перпендикулярной продольной оси;

• отбрасываем часть конструкции, лежащую по одну сторону от сечения;

• заменяем действие отброшенной части внутренним силовым фактором, соответствующим виду деформаций, который направляем в соответствии с принятым правилом знаков;

• составляя уравнение равновесия оставшейся части, находим искомый внутренний силовой фактор в виде функции от координаты сечения.

Продольная сила численно равна сумме проекций, приложенных к одной из отсеченных частей внешних сил на ось стержня (для прямолинейного стержня она совпадает в каждом сечении с осью Oх). Растяжение (сжатие) имеет место, если все внешние силы, действующие по одну сторону от данного поперечного сечения, сводятся к равно­действующей, направленной вдоль оси стержня (рис. 1.1 и 1.2). Одна и та же продольная сила N при действии на различные части стержня (левую или правую) имеет противоположные направления. Знак N зависит от характера вызываемой ею деформации. Продольная сила считается положительной, если вызывает растяжение элемента, и отрицательной, если вызывает сжатие.

На основе данных расчета, произведенного методом сечений, строится эпюра нормальных сил в виде графика распределения нормальной силы по длине бруса (задача 1). Характерно, что скачки на эпюре обусловлены наличием в соответствующих сечениях сосредоточенных сил, что, в свою очередь, может служить доказательством правильности выполненных построений.

Напряжения при растяжении-сжатии. Расчет на прочность. Так как при растяжении-сжатии в сечении элемента возникает только продольная сила, вектор которой направлен перпендикулярно плоскости поперечного сечения, то в этом сечении возникают только нормальные напряжения. Закон распределения этих напряжений вытекает из гипотезы плоских сечений, подтвержденной экспериментальными данными. Представим себе стержень, изготовленный из какого-либо податливого материала, на боковую поверхность которого нанесена система продольных и поперечных рисок (рис. 1.1, а). Эта ортогональная система рисок остается таковой и после приложения растягивающей нагрузки (рис. 1.1, б). Поперечные риски являются следами поперечных сечений на поверхности стержня и остаются прямыми и перпендикулярными к оси стержня, это свидетельствует о выполнении гипотезы плоских сечений (Бернулли). С учетом гипотезы об отсутствии поперечного взаимодействия продольных волокон приходим к выводу, что деформация растяжения стержня сводится к одноос­ному растяжению его продольных волокон, и в поперечном сечении стержня возникают лишь нормальные напряжения σ (рис. 1.2). Ортогональность продольных и поперечных рисок свидетельствует также об отсутствии сдвигов, а, следовательно, и связанных с ними касательных напряжений τ в поперечных и продольных сечениях стержня.

Рис.1.1. Модель растянутого стержня

Рис.1.2. Связь напряжения и усилия

Тогда продольная сила N, равная сумме проекций внутренних сил, действующих в данном поперечном сечении площадью А (рис. 1.2), очевидно, будет равна:

(1.1)

Это соотношение является уравнением равновесия (статики), связывающим продольную силу N и нормальное напряжение σ, которое в общем случае является функцией координат z и у и поэтому не может быть найдено из одного лишь уравнения статики. Таким образом, задача определения напряжений даже в самом простом случае деформирования стержня (растяжении или сжатии) оказывается статически неопределимой.

Необходимое для решения этой задачи дополнительное уравнение вытекает из гипотезы плоских сечений. Поскольку поперечные сечения стержня, оставаясь плоскими и перпендикулярными к оси стержня, в процессе деформирования лишь поступательно перемещаются вдоль оси стержня (что приводит к одинаковому удлинению всех продольных волокон), приходим к уравнению ε = const (ε – относительное удлинение), что следует из закона Гука для линейно упругого материала:

, (1.2)

откуда получим

. (1.3)

Таким образом, при растяжении (сжатии) призматического стержня нормальные напряжения равномерно распределены по поперечному сечению, а касательные напряжения в сечениях отсутствуют, что является следствием гипотезы плоских сечений. Указанное, несмотря на, казалось бы, очевидность и простоту, является фундаментальным результатом, справедливым, строго говоря, лишь для призматического стержня. Однако в инженерной практике его используют и для приближенной оценки нормальных напряжений в стержнях переменного сечения. При этом, чтобы погрешность формулы была невелика, необходимо, чтобы площадь поперечного сечения стержня изменялась достаточно плавно вдоль его оси.

Условие прочности при растяжении (сжатии) призматического стержня для стержня из пластического материала (т. е. материала, одинаково работающего на растяжение и сжатие) будет иметь вид:

, (1.4)

где – допускаемое напряжение.

Продольная сила N в условии (1.4) подставляется по модулю, так как знак в этом случае роли не играет. Для стержней из хрупких материалов, неодинаково сопротивляющихся растяжению и сжатию, знак напряжения имеет принципиальное значение, и условие прочности приходится формулировать отдельно для растяжения и сжатия:

,

,

где и – напряжения растяжения и сжатия, а и – соответствующие им допускаемые напряжения.

В практике инженерных расчетов, исходя из условия прочности, решаются три основные задачи механики материалов конструкций. В применении к случаю растяжения (сжатия) призматического стержня эти задачи формулируются следующим образом.

Проверка прочности (поверочный расчет). Этот расчет проводится, если нагрузка (в нашем случае ее представляет N), сечение стержня A и его материал ( ) заданы.

Необходимо убедиться, что выполняется условие прочности (1.4). Проверочный расчет заключается в том, что определяется фактический коэффициент запаса прочности п и сравнивается с нормативным коэффициентом запаса [n]:

, (1.5)

где – предельное (или опасное) напряжение, т. е. напряжение, вызывающее отказ элемента конструкции (напомним, что, например, для стержня из пластичного материала это предел текучести или условный предел текучести ).

Подбор сечения (проектный расчет). В этом расчете по заданной нагрузке определяются размеры поперечного сечения стержня из заданного материала ([ ] дано). Минимальное значение A получим, если в условии прочности (1.4) принять знак равенства:

. (1.6)

Определение допускаемой нагрузки, то есть максимального значения нагрузки, которое допускает данный элемент конструкции (А и даны) при выполнении условия прочности:

. (1.7)

Определение деформаций и перемещений. Определим упругие деформации стержня, предполагая, что изменение его длины при растяжении , называемое абсолютной продольной деформацией или удлинением, мало́ по сравнению с его первоначальной длиной. Тогда относительная продольная деформация будет равна:

. (1.8)

Учитывая, что, согласно закону Гука, для одноосного растяжения (сжатия) из выражения (1.2) для абсолютной деформации получаем:

. (1.9)

Произведение EA принято называть жесткостью поперечного сечения стержня при растяжении (сжатии), так как удлинение обратно пропорционально EA.

Рис.1.3. Модели продольной и поперечной деформаций

Как показывают эксперименты, при растяжении стержня размеры его поперечного сечения уменьшаются, а при сжатии – увеличиваются. Это явление получило название эффекта Пуассона.

По аналогии с продольной деформацией изменение размеров поперечного сечения (на рис. 1.3 ) будем называть абсолютной поперечной деформацией, а – относительной поперечной деформацией. Относительные продольная и поперечная деформации, имеющие противоположные знаки, связаны между собой коэффициентом , являющимся константой материала и называемым коэффициентом поперечной деформации или коэффициентом Пуассона:

. (1.10)

Как известно, для изотропного материала .

Формула (1.9) для удлинения стержня применима только в случае, когда по длине стержня ни жесткость поперечного сечения, ни продольная сила не изменяются (EA = const, N = const). Удлинение стержня со ступенчатым изменением EA и N может быть определено как сумма удлинений ступеней, у которых EА и N постоянны:

, (1.11)

где индекс k у модуля продольной упругости означает, что участки стержня могут быть изготовлены из различных материалов.

ЗАДАЧА 1

Для ступенчатого стержня, расчетная схема которого показана на рис. 1.4, требуется: построить в выбранных масштабах эпюры внутренних усилий, нормальных напряжений и осевых перемещений; из условия прочности подобрать размеры поперечного сечения.

Дано: А₁/А₂ = 1,2 ; P₁ = 64 кН , P₂ = 42 кН , P₃ = 2,1 P₂ ,

= 160 МПа , Е МПа.

Решение

1. Построение эпюры продольных сил.

Разбиваем стержень на участки, границами которых являются поперечные сечения, в которых или приложены силы, или изменяется площадь поперечного сечения стержня. Таких участков имеется четыре.

Рис.1.4. Расчетная схема ступенчатого стержня

Определяем внутренние продольные усилия по участкам, используя метод сечений [1 – 9]. Согласно этому методу, мысленно проводим сечение по участку, прикладываем к отсеченной части в сторону от сечения силу и определяем ее из условия статического равновесия отсеченной части по формуле:

,

где суммируются все силы, действующие на отсеченную часть. При этом силы берутся с плюсом, если они растягивают относительно проведенного сечения отсеченную часть стержня, и с минусом, если они сжимают отсеченную часть. Использование этой формулы, даёт возможность не рисовать для каждого участка отсеченную часть, чтобы рассмотреть ее статическое равновесие. В итоге усилия по участкам будут равны:

1-й участок кН;

2-й участок кН;

3-й участок кН;

4-й участок кН.

Знак минус у означает, что усилие сжимающее (участки 1 – 3 сжаты), знак плюс – усилие растягивающее (участок 4 растянут (рис. 1.5, а)).

Строим эпюру . Для этого проводим вертикальную ось и перпендикулярно ей в выбранном масштабе откладываем в виде ординат значения на участках (рис. 1.5, а).

2. Построение эпюры нормальных напряжений и определение размеров поперечного сечения по участкам.

Для построения эпюры нормальных напряжений определяем напряжения по формуле:

,

где А – площадь поперечного сечения на участке.

При этом, используя зависимость , выразим в виде отношения силы к площади . Имеем по участкам:

1. ;

2. ;

3. ;

4. .

Из условия прочности [1 – 9]:

,

проводя проектный расчет, находим площадь . Как видно из рис.1.5, наибольшее напряжение действует на четвертом участке. Тогда

.

Отсюда находим:

и .

Подставляя полученные значения сил в выражения для напряжений, получим:

МПа;

МПа;

МПа;

МПа.

По полученным данным строим эпюру нормальных напряжений (см. рис. 1.5, б).

Рис. 1.5. Построение эпюр продольных сил, нормальных напряжений и абсолютных удлинений

3. Построение эпюры абсолютных удлинений.

Далее определяем перемещения точек стержня. В пределах участков перемещения изменяются по линейному закону [1 – 9, 11]:

где – координата точки, в которой определяются перемещения (она изменяется в пределах , – длина участка). Следовательно, для построения эпюры достаточно определить перемещения границ участков по формуле:

Начинать следует с опоры стержня, поскольку перемещение ее известно и равно нулю. Перемещение верхней границы четвертого участка равно удлинению этого участка:

мм.

Перемещение верхней границы третьего участка равно сумме удлинений четвертого и третьего участков:

=

мм.

Аналогично для второго и первого участков:

мм;

мм.

Перемещение равно полному удлинению стержня. Величина положительна, следовательно, стержень удлиняется на мм. Откладывая перпендикулярно оси эпюры значения перемещений границ участков и соединения их прямыми, строим эпюру (рис. 1.5, в).

Вопросы для самопроверки

1. Что называется растяжением, сжатием?

2. Какая продольная сила считается положительной, и как она направлена?

3. Каким методом определяется продольная сила? В чем сущность этого метода? Правило знаков.

4. Как и для чего строится эпюра продольных сил?

5. Что называется напряжением? Для чего вводится это понятие?

6. Какие напряжения вы знаете?

7. Что такое допускаемое напряжение?

8. Что учитывает коэффициент запаса?

9. Для чего и как записывается условие прочности? Какие задачи оно позволяет решать?

10. В чем сущность гипотезы плоских сечений? Как онa используется?

11. По какой формуле определяются нормальные напряжения?

12. Как определяется знак нормальных напряжений?

13. Что называется деформацией?

14. Какие виды деформаций вы знаете?

15. Каким законом связаны деформации и напряжения, перемещения и силы?

16. Что такое коэффициент Пуассона?

17. Что характеризует модуль нормальной упругости (модуль упругости 1-го рода) ?

18. Что такое жесткость при растяжении-сжатии?

19. Какие механические характеристики материалов вы знаете? Как они определяются и что характеризуют?

20. Какие материалы называются пластичными, хрупкими?

2. РАСЧЕТЫ НА ПРОЧНОСТЬ И ЖЕСТКОСТЬ ПРИ КРУЧЕНИИ

Построение эпюр крутящих моментов. Кручение – простейший вид деформаций, при котором к брусу (валу) прикладываются внешние пары сил в плоскостях, совпадающих с поперечным сечением вала, а в последних возникает только внутренний крутящий момент.

Методика построения эпюры крутящих моментов аналогична вышеприведенной методике при растяжении-сжатии, основанной на методе сечений (раздел 1). При этом участком является расстояние между сечениями, в которых к валу приложены внешние пары сил (их принято называть скручивающими моментами).

Крутящий момент по определению равен сумме моментов внутренних сил относительно продольной оси стержня Oх (рис. 2.1). Нормальные силы, параллельные оси Oх, вклада в крутящий момент не вносят. С силами, лежащими в плоскости поперечного сечения стержня (интенсивности этих сил – касательные напряжения и ) М_х связывает вытекающее из его определения уравнение равновесия (статики) [1 – 7, 9, 11]:

. (2.1)

Рис.2.1. Связь крутящего момента с касательными напряжениями

Условимся считать M_х положительным, если со стороны отброшенной части стержня видим его направленным против часовой стрелки (рис. 2.2). Это правило проиллюстрировано на рис. 2.1 и в указанном соотношении, где крутящий момент М_х принят положительным. Численно крутящий момент равен сумме моментов внешних сил, приложенных к отсеченной части стержня, относительно оси Ох.

Рис.2.2. Иллюстрация положительного и отрицательного крутящего момента

Напряжения при кручении. Расчет на прочность. Рассмотрим кручение призматических стержней кругового поперечного сечения. Исследование деформаций упругого стержня с нанесенной на его поверхности ортогональной сеткой рисок (рис. 2.3) позволяет сформулировать следующие предпосылки теории кручения этого стержня:

• поперечные сечения остаются плоскими (выполняется гипотеза Бернулли);

• расстояния между поперечными сечениями не изменяются, следовательно ;

• контуры поперечных сечений и их радиусы не деформируются. Это означает, что поперечные сечения ведут себя как жесткие круговые пластинки, поворачивающиеся при деформировании относительно оси стержня Ох. Отсюда следует, что любые деформации в плоскости пластинки равны нулю, в том числе и ;

• материал стержня подчиняется закону Гука.

Учитывая, что , из обобщенного закона Гука [1–7] получаем . Это означает, что в поперечных сечениях стержня возникают лишь касательные напряжения , а согласно закону парности касательных напряжений, равные им напряжения действуют и в сопряженных продольных сечениях. Следовательно, напряженное состояние стержня – чистый сдвиг.

а)

б)

Рис.2.3. Иллюстрация кручения: а) исходное и б) деформированное состояния

Касательные напряжения при кручении определяются в соответствии с законом Гука для чистого сдвига (рис. 2.4):

. (2.2)

Рис.2.4. Расчетная модель определения касательных напряжений

Рис.2.5. Распределение касательных напряжений при кручении

Здесь – погонный угол закручивания стержня, который остается пока неизвестным. Для его определения обратимся к условию статики, записав его в более удобной для данного случая форме:

. (2.3)

Подставляем (2.2) в (2.3), учитывая, что

, (2.4)

где J_ρ – полярный момент инерции поперечного сечения [1 – 7].

Получим

. (2.5)

Для круга с диаметром d значение определяется

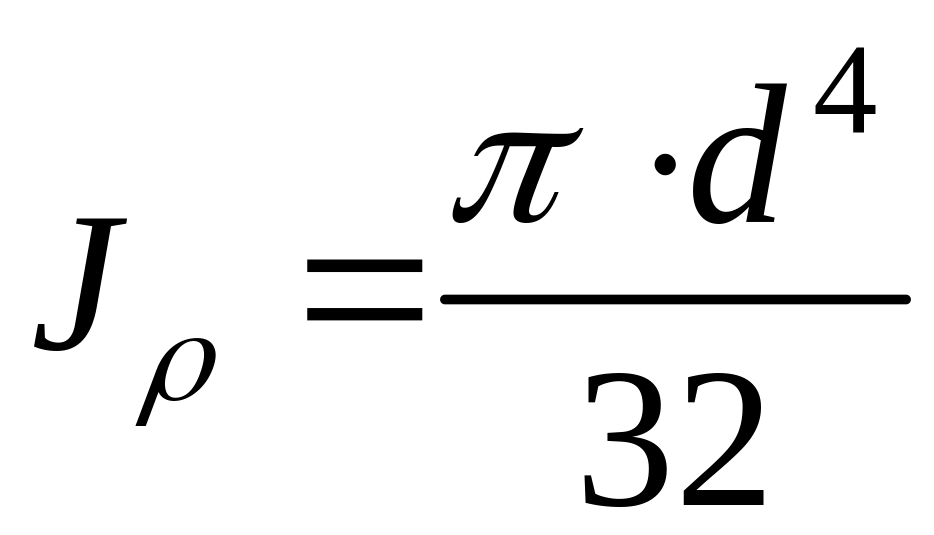. (2.6)

Рис.2.6. Распределение напряжений для кольцевого сечения

Подставляя выражение (2.5) в (2.2), получаем формулу для касательных напряжений при кручении призматического стержня кругового поперечного сечения:

. (2.7)

Как видно из (2.7), сдвиги и касательные напряжения пропорциональны расстояниям от оси стержня.

Наибольшие касательные напряжения возникают у внешней поверхности стержня, т. е. при :

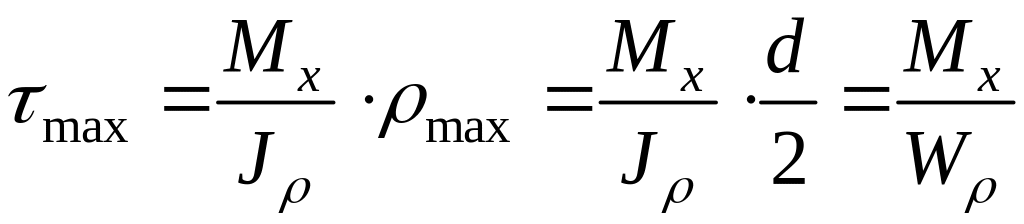, (2.8)

где W_ρ — момент сопротивления при кручении или полярный момент сопротивления [1 – 7]:

. (2.9)

Полярный момент сопротивления, стоящий в знаменателе в выражении (2.8) для максимальных касательных напряжений, очевидно, является геометрической характеристикой сечения, а условие прочности стержня при кручении принимает вид:

. (2.10)

где – допускаемое напряжение кручения.

Как показали эксперименты и точное решение этой задачи в теории упругости, все гипотезы, сформулированные ранее для стержня со сплошным круговым сечением, остаются справедливыми и для стержня кольцевого поперечного сечения (рис. 2.6). Поэтому все выведенные ранее формулы пригодны для расчета стержня кольцевого сечения с той лишь разницей, что полярный момент инерции определяется как разность моментов инерции кругов с диаметрами D и d:

, (2.11)

где , а момент сопротивления определяется по формуле:

. (2.12)

Учитывая линейный характер изменения касательных напряжений по радиусу (рис. 2.6) и связанное с этим лучшее использование материала, кольцевое сечение следует признать наиболее рациональным при кручении стержня. Коэффициент использования материала тем выше, чем меньше относительная толщина трубы.

Определение деформаций и перемещений. Мерой деформации стержня при кручении является относительный угол закручивания стержня, определяемый по формуле (2.5) и обозначаемый θ. Поскольку величина стоит в знаменателе формулы и при заданной нагрузке тем меньше, чем больше , последнюю называют жесткостью поперечного сечения при кручении.

Пользуясь формулой (2.5) для определения угла закручивания элемента длиной dх, найдем полный угол закручивания стержня длиной l:

. (2.13)

В случае, если по длине стержня М_х и постоянны, получаем:

. (2.14)

Отметим, что полученные формулы по структуре аналогичны формулам для деформаций при растяжении-сжатии стержня (раздел 1).

ЗАДАЧА 2

Для ступенчатого вала круглого поперечного сечения следует определить из условий прочности и жесткости диаметры всех участков вала, построить эпюры крутящих моментов, касательных напряжений и абсолютных углов закручивания.

Дано: расчетная схема вала приведена на рис. 2.7, а, где

кН·м, кН·м, кН·м, кН·м = МПа, МПа, град/м.

Рис. 2.7. Построение эпюр крутящих моментов, касательных напряжений и абсолютных углов закручивания

Решение

1. Построение эпюры крутящих моментов и определение диаметров.

Вал имеет четыре участка, границами которых являются характерные поперечные сечения (сечения, в которых приложены моменты или изменяется диаметр вала). Из условия статического равновесия:

находим реактивный момент . В настоящее время крутящий момент в большинстве случаев обозначают как T, поэтому крутящие моменты в поперечных сечениях определяем по участкам методом сечений по формуле , где суммируются все внешние моменты, действующие на отсеченную часть. В сумме берутся с плюсом, если они скручивают вал против часовой стрелки при взгляде со стороны сечения, и с минусом, если они скручивают вал по часовой стрелке [1 – 3, 5, 7, 9, 11].

Проводим сечение по первому участку и рассматриваем равновесие левой отсеченной части. Получаем на первом участке кН·м.

Аналогично на 2 – 4-м участках:

кН·м;

кН·м;

кН·м.

Если на 4-м участке рассмотреть равновесие правой отсеченной части, то получим:

кН·м.

Далее в масштабе строим эпюру крутящих моментов (рис. 2.7, б).

Диаметры валов на участках подбираем из условий прочности и жесткости [1 – 11]. Из условия прочности:

.

Из условия жесткости:

,

где – наибольший по модулю крутящий момент на участке .

На 1-м, 2-м участках кН·м.

Из условия прочности:

м = 173 мм;

из условия жесткости:

м = 196 мм.

Принимаем наибольшее значение мм, округляя его до стандартного значения мм.

Аналогично для 3-го, 4-го участков , где кН·м.

Из условия прочности:

м = 202 мм;

из условия жесткости:

= м = 220 мм.

Принимаем наибольшее значение мм (соответствует стандартному).

2. Построение эпюры касательных напряжений.

В соответствии с полученными значениями диаметров по формуле:

,

где – полярный момент сопротивления,

определяем касательные напряжения по участкам [1 – 11]:

МПа;

МПа;

МПа;

МПа.

По результатам расчета строим эпюру касательных напряжений (рис. 2.7, в).

3. Построение эпюры абсолютных углов закручивания.

Далее определяем углы закручивания вала. На участке с постоянными значениями и углы закручивания изменяются по линейному закону [1 – 7, 11]:

, ,

где i – индекс участка, – осевая координата, – полярный момент инерции поперечного сечения. Следовательно, для построения эпюры углов закручивания вала достаточно определить углы закручивания участков вала:

,

где = 1,2,3,4, – длина i-го участка.

Углы закручивания участков вала равны углам поворота левого края участка относительно правого края, так как в дальнейшем для построения эпюры абсолютных углов закручивания они будут алгебраически суммироваться, начиная от сечения, в котором действует реактивный момент M_о (рис. 2.7).

Имеем по участкам:

рад;

рад;

рад;

рад.

Строим эпюру углов закручивания вала. На правом крае вала в сечении К, в котором действует реактивный момент М₀, угол закручивания условно принимается равным нулю. На левом крае 4-го участка (рис. 2.7) угол закручивания равен . Итак,

,

рад.

На левом крае третьего участка

рад.

На левом крае второго участка

рад.

На левом крае вала

рад.

По результатам расчета строим эпюру абсолютных углов закручивания (рис. 2.7, г).

Если вал нагружен еще и распределенной нагрузкой , то момент от распределенной нагрузки в сечении с координатой равен (рис. 2.8):

,

а формула для определения угла закручивания участка распределенной нагрузкой будет иметь вид [2,5, 6, 7]:

Рис.2.8. К построению эпюр крутящих моментов и углов закручивания при действии равномерно распределенной нагрузки

Вопросы и задания для самопроверки

1. Что называется кручением?

2. Как определяются внутренние крутящие моменты? Правило знаков.

3. Как и для чего строится эпюра крутящих моментов?

4. В чем суть гипотезы плоских сечений при кручении? Для чего она нужна?

5. Какие напряжения действуют в поперечных сечениях вала при кручении? По какой формуле они определяются?

6. Как распределены в поперечных сечениях касательные напряжения?

7. Как определяются наибольшие касательные напряжения?

8. Что такое полярный момент инерции? По какой формуле он определяется?

9. Что такое жесткость при кручении?

10.Что такое полярный момент сопротивления? Его формула?

11. Что такое относительный угол закручивания? Как он определяется?

12. Чему равны главные напряжения при кручении? Где они действуют?

13. Условие прочности при кручении. Какие задачи можно решать с его помощью?

14. Какие виды разрушений возможны при кручении?

15. Запишите условие жесткости при кручении.

16. Почему иногда валы изготовляют полыми?

17. В каком виде записывается закон Гука при сдвиге?

18. Что такое модуль сдвига (модуль упругости 2-го рода)?

19. Какова связь допускаемых нормального и касательного напряжений?

20. К какому виду (по классификации) можно отнести напряжения в поперечном сечении вала при кручении?

3. РАСЧЕТ НА ПРОЧНОСТЬ БАЛОК ПРИ ИЗГИБЕ

Построение эпюр изгибающих моментов и поперечных сил. Плоский поперечный (прямой ) изгиб – вид деформаций, при котором в поперечном сечении элемента действуют два внутренних силовых фактора: изгибающий момент и поперечная сила. Данный простой вид сопротивления реализуется в случае, когда внешние силы приложены перпендикулярно продольной оси бруса (балки) и расположены в одной из главных плоскостей в соответствии с конфигурацией поперечного сечения балки.

При прямом чистом изгибе в поперечном сечении стержня возникает только один силовой фактор – изгибающий момент М_z (рис. 3.1). Так как Q_y=dM_z /dz=0, то M_z=const , поэтому чистый прямой изгиб может быть реализован при загружении стержня парами сил, приложенными в торцевых сечениях стержня.

Рис.3.1. Связь внутреннего усилия и напряжения

Эпюры изгибающих моментов и поперечных сил строятся методом сечений (раздел 1) по участкам. Участком считается расстояние между сечениями, в которых действуют внешние силовые факторы (сосредоточенные силы и пары сил). Особо выделяются участки действия равномерно распределенной нагрузки. При построении эпюр в балках приняты следующие правила знаков:

• изгибающий момент считается положительным, если он стремится вызвать сжатие в верхних волокнах балки;

• поперечная сила считается положительной, если она стремится повернуть элемент по ходу часовой стрелки [1 – 7, 9 – 11].

Нормальные напряжения при чистом изгибе. Условие прочности. Поскольку изгибающий момент M_z по определению равен сумме моментов внутренних сил относительно оси Оz, то с нормальными напряжениями его связывает вытекающее из этого определения уравнение статики [1–7]:

. (3.1)

Для определения закона распределения нормальных напряжений по сечению проанализируем деформации модели стержня из низкомодульного материала, на боковой поверхности которого нанесена сетка продольных и поперечных рисок (рис. 3.2). Поперечные риски при изгибе стержня парами сил, приложенными в торцевых сечениях, остаются прямыми и перпендикулярными к искривленным продольным рискам, это позволяет сделать вывод о выполнении гипотезы плоских сечений, которая, как показывает решение этой задачи методами теории упругости, перестает быть гипотезой, становясь точным фактом – законом плоских сечений. Замеряя изменение расстояний между продольными рисками, приходим к выводу о справедливости гипотезы о ненадавливании продольных волокон .

Ортогональность продольных и поперечных рисок до и после деформирования (как отражение действия закона плоских сечений) указывает также на отсутствие сдвигов (касательных напряжений) в поперечных и продольных сечениях стержня.

Рис. 3.2. Модель чистого изгиба

Таким образом, чистый прямой изгиб призматического стержня сводится к одноосному растяжению или сжатию продольных волокон напряжениями . При этом часть волокон находится в зоне растяжения (на рис. 3.2 это нижние волокна), а другая часть – в зоне сжатия (верхние волокна). Эти зоны разделены нейтральным слоем (п – п), не меняющим своей длины, напряжения в котором равны нулю. Учитывая сформулированные выше предпосылки и полагая, что материал стержня линейно-упругий, т. е. закон Гука в этом случае имеет вид , получены формулы для кривизны нейтрального слоя ( – радиус кривизны) и нормальных напряжений . Предварительно отметим, что постоянство поперечного сечения призматического стержня и изгибающего момента (M_z=сonst), обеспечивает постоянство радиуса кривизны нейтрального слоя по длине стержня (рис. 3.3, а), нейтральный слой (п – п) описывается дугой окружности.

Рассмотрим призматический стержень в условиях прямого чистого изгиба (рис. 3.3, а) с поперечным сечением, симметричным относительно вертикальной оси Оу. Это условие не отразится на конечном результате (чтобы прямой изгиб был возможен, необходимо совпадение оси Оу с главной осью инерции поперечного сечения, которая и является осью симметрии). Ось Oz поместим на нейтральном слое, положение которого заранее неизвестно.

Рис. 3.3. Фрагмент чистого изгиба бруса: а) расчетная схема, б) деформации и напряжения

Рассмотрим вырезанный из стержня элемент длиной dх, который в масштабе с искаженными в интересах наглядности пропорциями изображен на рис. 3.3, б. Поскольку интерес представляют деформации элемента, определяемые относительным смещением его точек, одно из торцевых сечений элемента можно считать неподвижным. Ввиду малости считаем, что точки поперечного сечения при повороте на этот угол перемещаются не по дугам, а по соответствующим касательным.

Вычислим относительную деформацию продольного волокна АВ, отстоящего от нейтрального слоя на у:

.

Из подобия треугольников СОО₁ и О₁ВВ₁ следует, что

.

Продольная деформация оказалась линейной функцией расстояния от нейтрального слоя, что является прямым следствием закона плоских сечений:

. (3.2)

Тогда нормальное напряжение, растягивающее волокно АВ, согласно закону Гука, будет равно:

. (3.3)

Эта формула не пригодна для практического использования, так как содержит две неизвестные: кривизну нейтрального слоя и положение нейтральной оси Ох, от которой отсчитывается координата у.

Определим кривизну нейтрального слоя, подставляя (3.3) в (3.1):

, (3.4)

где , (3.5)

J_z – главный центральный момент инерции относительно оси О. Таким образом, для кривизны нейтрального слоя получаем формулу:

. (3.6)

Кривизна нейтрального слоя является мерой деформации стержня при прямом чистом изгибе: тем меньше, чем больше величина EJ_z, называемая жесткостью поперечного сечения при изгибе (изгибной жесткостью – по аналогии с крутильной жесткостью и жесткостью поперечного сечения при растяжении-сжатии EA).

Подставляя (3.6) в (3.3), получаем формулу для нормальных напряжений в виде:

, (3.7)

которая была впервые получена Ш. Кулоном в 1773 г. Для согласования знаков изгибающего момента М_z и нормальных напряжений в правой части формулы (3.7) ставится знак минус, так как при M_z>0 нормальные напряжения при y>0 оказываются сжимающими. Однако в практических расчетах удобнее, не придерживаясь формального правила знаков, определять напряжения по модулю, а знак ставить по смыслу.

Таким образом, нормальные напряжения при чистом изгибе призматического стержня являются линейной функцией координаты у и достигают наибольших значений в волокнах, наиболее удаленных от нейтральной оси (рис. 3.4), т. е.

. (3.8)

Рис.3.4. Распределение нормальных напряжений

Здесь введена геометрическая характеристика , имеющая размерность м³ и получившая название момента сопротивления при изгибе. Поскольку при заданном M_z максимальные напряжения тем меньше, чем больше W_z, то момент сопротивления является геометрической характеристикой прочности поперечного сечения при изгибе.

Приведем примеры вычисления моментов сопротивления для простейших форм поперечных сечений. Для прямоугольного поперечного сечения (рис. 3.5, а) имеем J_z=bh³/12, y_max = h/2 , тогда

. (3.9)

Аналогично для круга (рис. 3.5, a J_z = πd⁴/64, y_max = d/2) получаем:

. (3.10)

Для кругового кольцевого сечения (рис. 3.5, в), получаем:

, (3.11)

где .

Рис. 3.5. Конфигурации поперечных сечений бруса

Итак, обобщая вышесказанное, поскольку ось z является нейтральной (рис. 3.5), максимальные нормальные напряжения в сечении с изгибающим моментом M_z определяются по формуле:

. (3.12)

Этой формулой удобно пользоваться для расчета балок пластичного материала в упругой области, одинаково работающего на растяжение и сжатие. Поскольку знак напряжения в этом случае не имеет значения, напряжения вычисляются по модулю, и условие прочности при изгибе балки в форме призматического стержня принимает вид:

, (3.13)

где – максимальное значение изгибающего момента (легко определяемое по его эпюре), – допускаемое напряжение на простое растяжение (сжатие). Напомним, что чистый изгиб балки сводится к растяжению и сжатию ее волокон (неравномерному в отличие от деформации растяжения (сжатия) призматического стержня, при котором ).

Рис.3.6. Модель изгиба хрупкого материала

При расчете балок из хрупких материалов следует различать наибольшие растягивающие max и наибольшие сжимающие напряжения (рис. 3.6), которые также определяются по модулю непосредственно и сравниваются с допускаемыми напряжениями на растяжение и сжатие . Условия прочности в этом случае будут иметь вид:

, (3.14)

. (3.15)

ЗАДАЧА 3

Для двухопорной балки требуется составить аналитические выражения поперечных сил Q и изгибающих моментов М по участкам, построить эпюры Q, М. Также необходимо из условия прочности по нормальным напряжениям определить размеры поперечного сечения балки заданной формы; определить нормальные и касательные напряжения в точке А поперечного сечения, для которого Q и М имеют наибольшие значения.

Дано: расчетная схема балки приведена на рис. 3.7, где q = 24 кН/м,

F = 38 кН, М₁ = 51 кН м; допускаемое напряжение = 100 МПа.

Решение

1. Определение опорных реакций.

Определяем реакции опор R_A, R_B. Для этого составляем уравнения статики, приравнивая к нулю суммы моментов относительно точек А и В:

.

.

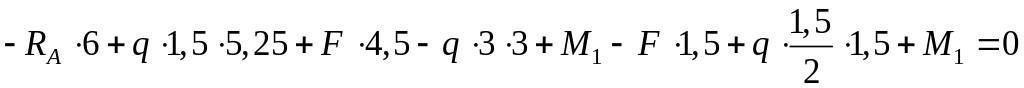Отсюда находим кН, кН.

Реакция получилась со знаком минус, следовательно, в действительности она направлена вниз.

Рис. 3.7. Построение эпюр изгибающих моментов и поперечных сил в балке

Проверка реакций: составляем уравнение статики, приравнивая к нулю сумму проекций всех сил на ось у.

.

Уравнение удовлетворяется тождественно, следовательно, реакции определены правильно.

2. Построение эпюр изгибающих моментов и поперечных сил.

Составляем выражения поперечных сил и изгибающих моментов по участкам, пользуясь методом сечений и формулами:

где – проекции внешних сил, действующих на отсеченную часть; – моменты от нагрузки, действующей на отсеченную часть [1 – 3,7, 9, 14 – 19].

Правило знаков: берутся с плюсом, если силы направлены по оси y , и с минусом, если направлены против оси y, правой декартовой системы координат; берётся с плюсом, если он изгибает балку относительно сечения выпуклостью вниз, и с минусом – при изгибе балки выпуклостью вверх (правило дождя) [1,2,3, 7 – 9].

1-й участок: (0 < х₁< 1,5 м ).

Рассматриваем левую отсеченную часть (рис.3.8)

Рис. 3.8. Расчетная схема левой отсеченной части на 1-м участке

Запишем уравнения для поперечных сил и изгибающих моментов:

Q = R_A – q∙х₁, M = R_A х₁ – q∙х_1∙(х₁/2).

Строим эпюры Q, М. Для этого вычисляем значения Q и М в начале и конце участка, а также в промежуточном сечении, соответствующем середине участка, при х₁ = 0,75 м:

Q(х₁=0) = R₁ = 36 кН, М (х₁ = 0) = 0.

, кН·м,

кН·м.

Эпюры M и Q приведены на рис. 3.7. Заметим, что эпюра выпуклостью направлена против направления действия распределенной нагрузки q (правило обтекания или правило дождя).

2-й участок: (0<х₂<3 м).

Расчетная схема изображается аналогично приведенной на рис. 3.8. Проводя сечение на расстоянии х₂ от левого края участка, получаем по формулам следующие результаты:

,

.

кН,

кН,

кН·м,

кН·м.

Эпюры M и Q для 2-го участка представлены на рис. 3.7. Заметим, что эпюра Q пересекает базу, т.е. на 2-м участке имеется такое сечение, в котором поперечная сила равна нулю. В соответствии с дифференциальной зависимостью

в этом сечении на эпюре М должен быть минимум (поперечная сила меняет знак с « – » на «+» (рис. 3.7) [1 – 9,11]. Приравнивая к нулю выражение для Q, находим х₂, при котором М имеет минимальное значение:

,

откуда м

кН·м.

3-й участок: (0 < х₃ < 1,5 м).

На этом участке удобнее рассматривать правую отсеченную часть (рис. 3.9). Уравнения для изгибающих моментов и поперечных сил:

,

.

Рис.3.9. Расчетная схема правой отсеченной части на 3-м участке

Определим в характерных сечениях значение поперечных сил и изгибающих моментов:

кН, кН,

кН·м,

кН·м,

кН.

По данным расчета строим эпюры Q и M. Заметим, что скачки на эпюре Q равны сосредоточенным силам F, а на эпюре М – сосредоточенным моментам М (рис. 3.7).

3. Определение размеров поперечного сечения.

Сечение задано в виде прямоугольника с тремя отверстиями (рис. 3.10). Условие прочности по нормальным напряжениям:

,

где – наибольшее по модулю значение изгибающего момента [1–11]. Согласно построенной эпюре = 51 кН м.

Осевой момент сопротивления относительно нейтральной оси

,

где – момент инерции поперечного сечения относительно нейтральной оси z, y_max – расстояние от оси z до крайнего волокна [1,2,3]. Имеем ;

a⁴;

W_z = 9,87 a³.

Подставляя , в условие прочности, находим:

, м

Принимаем с запасом а = 0,04 м = 4 см.

Рис. 3.10. К определению размеров поперечного сечения балки

4. Определение нормальных и касательных напряжений в точке А.

Для определения нормальных и касательных напряжений в точке А (рис. 3.10) находим значения осевого момента сопротивления и координаты точки относительно нейтральной оси:

см⁴, см.

Нормальное напряжение:

_.

Касательное напряжение определяем по формуле Журавского [1,2,3,4]:

Здесь S_z(y) – статический момент части сечения (прямоугольник с двойной штриховкой), b (y) = 2а.

,

МПа.

Примечание. Если задана консольная балка, то реакции опор можно не определять. Построение эпюр Q и М следует начинать со свободного края. В остальном расчет выполняется так же, как и для двухопорной балки. В случае, когда поперечное сечение прокатного профиля (двутавр, швеллер и т.д.), из условия прочности определяется момент сопротивления, по которому из таблиц сортамента прокатной стали подбирается номер профиля.

В рассмотренном случае (при = 160 МПа)

см³.

По сортаменту прокатной стали [12–17] подбираем двутавр № 24a, имеющий W_z = 317 см³ .

Вопросы для самопроверки

1. Что называется чистым изгибом?

2. Что называется поперечным изгибом?

3. Что такое прямой изгиб? Что такое косой изгиб?

4. Как определяются поперечная сила Q и изгибающий момент М? Правило знаков.

5. Как строятся эпюры Q и М?

6. Чему равны скачки на эпюрах?

7. Как проверяется правильность построения эпюр?

8. Какие существует дифференциальные зависимости между q, Q, М?

9. Как изменяются Q, М на участках балки, свободных от равномерно распределенной нагрузки?

10. Как изменяются Q , М на участках балки с равномерно распределенной нагрузкой q?

11. Как используется гипотеза плоских сечений при изгибе?

12. Как определяются нормальные напряжения при изгибе? Как они распределяются по сечению?

13. Как определяются максимальные нормальные напряжения?

14. Что такое нейтральная линия, нейтральный слой?

15. Что такое осевой момент сопротивления?

16. Какой вид имеет условие прочности при изгибе? Какие типы задач можно решать с его помощью?

17. Как определяются касательные напряжения при поперечном изгибе? Как они изменяются по сечению балки?

18. Как определяются главные напряжения при изгибе?

19. Каким (по классификации) является напряженное состояние при изгибе?

20. Как выглядит условие прочности балки по касательным напряжениям и когда оно используется?

21. Как выглядит условие прочности по главным напряжениям?

22. Каковы рациональные формы поперечных сечений балок?

4. ПОСТРОЕНИЕ ЭПЮР ИЗГИБАЮЩИХ МОМЕНТОВ, ПОПЕРЕЧНЫХ И ПРОДОЛЬНЫХ СИЛ В ПЛОСКИХ РАМАХ

Особую группу стержневых систем составляют плоские системы. У плоской рамы оси всех составляющих элементов до и после деформации расположены в одной плоскости. В этой же плоскости действуют все внешние силы, включая и реакции опор (рис. 4.1, а).

Наряду с плоскими рассматриваются так называемые плоско-пространственные системы. Для такого рода систем оси составляющих элементов в недеформированном состоянии располагаются, как и для плоских систем, в одной плоскости. Внешние же силовые факторы действуют в плоскостях, перпендикулярных к этой плоскости (рис. 4.1, б). Стержневые системы, не относящиеся к двум указанным классам, называются пространственными (рис.4.1, в) [1 – 7, 9, 11]. Особенности расчета пространственных систем рассмотрены в разделе 7.

Рис.4.1. Расчетные схемы рамных конструкций: а) плоская, б) плоскопространственная, в) пространственная

Рамы принято разделять на статически определимые и статически неопределимые. Под статически определимой понимается такая кинематически неизменяемая система, для которой все реакции опор могут быть определены при помощи уравнений равновесия, а затем при найденных опорных реакциях методом сечений могут быть найдены также и внутренние силовые факторы в любом поперечном сечении. Под статически неопределимой системой имеется в виду такая, опять же кинематически неизменяемая система, для которой определение внешних реакций и внутренних силовых факторов не может быть произведено при помощи метода сечений и уравнений равновесия. Расчету статически неопределимых систем посвящены разделы 5 и 6.

В сечениях плоских рам при изгибе возникают три внутренних силовых фактора: изгибающий момент, поперечная сила и продольная сила. Как и в предыдущих разделах, эпюры изгибающих моментов, поперечных и продольных сил в плоских рамах строятся методом сечений (раздел 1) по участкам. Участком считается расстояние между сечениями, в которых действуют внешние силовые факторы (сосредоточенные силы и пары сил). Особо выделяются участки действия равномерно распределенной нагрузки. При построении эпюр в рамах приняты следующие правила знаков:

• изгибающий момент считается положительным, если он стремится вызвать сжатие во внешних волокнах рамы;

• поперечная сила считается положительной, если она стремится повернуть элемент по ходу часовой стрелки;

• продольная сила считается положительной, если она направлена от сечения, т. е. стремится вызвать растяжение [1 – 7, 9, 11].

ЗАДАЧА 4

Для ломаного стержня (рамы) необходимо построить эпюры изгибающих моментов, продольных и поперечных сил.

Дано: расчетная схема рамы приведена на рис. 4.2, где

м, кН, кН·м.

Рис. 4.2. Расчетная схема рамы

Решение

1. Определение опорных реакций.

Определяем реакции опор из уравнений равновесия рамы:

, ,

откуда кН.

,

откуда кН.

, , откуда кН.

2. Построение эпюр внутренних силовых факторов.

Эпюры внутренних силовых факторов строим методом сечений по участкам [1 – 11]. Рама имеет 8 участков (рис. 4.2). Начало локальной системы координат помещаем в начале участка, ось х совмещаем с продольной осью элемента (рис. 4.3, 4.4, 4.5). Эпюры приведены на рис. 4.6.

1-й участок: .

кН, кН, , кН·м

Рис. 4.3. Расчетная схема нижней отсеченной части рамы на 1-м участке

2-й участок: .

, кН, кН·м.

Рис. 4.4. Расчетная схема левой отсеченной части рамы на 2-м участке

3-й участок: .

, кН, , кН·м, кН·м.

Рис. 4.5. Расчетная схема нижней отсеченной части рамы на 3-м участке

Рис. 4.6. Построение эпюр изгибающих моментов, поперечных и продольных сил в рамах