Выпуклость и точки перегиба графика функции

Определение. График функции y = f(x) имеет на интервале (а, b) выпуклость, направленную вниз (вверх), если он расположен не ниже (не выше) любой каса­тельной к графику функции на (а, b) (рис.5).

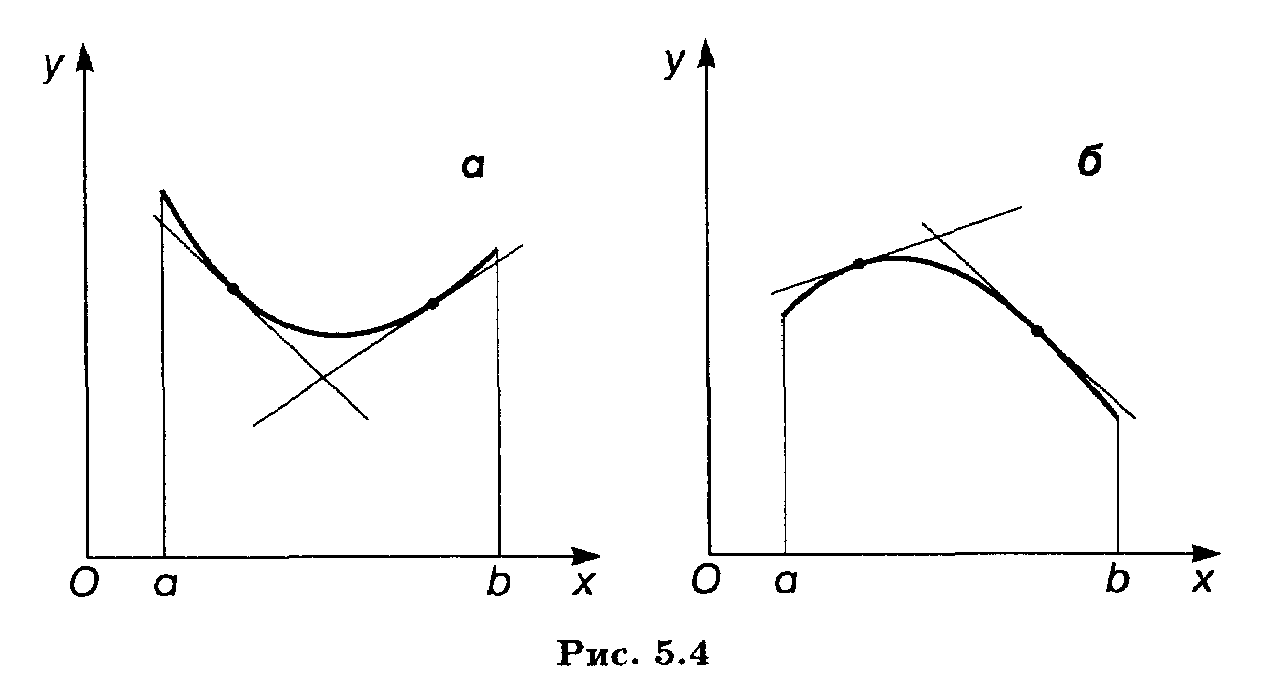
Рис.5

ТЕОРЕМА. Если функция у = f(х) имеет на интервале (а, b) вторую производную и f"(x) ≥ 0 (f"(x) ≤ 0) на (а, b), то график функции имеет на (а, b) выпуклость, направленную вниз (вверх).

Определение. Точка М(x₀, f(x₀)) называется точкой пере­гиба графика функции у = f(x), если в точке М график имеет касательную и существует такая окрестность точки x₀, в пре­делах которой график функции f(x) имеет разные направления выпуклости.

В точке перегиба касательная пересекает график функции, поскольку он переходит с одной стороны касательной на дру­гую, т.е. "перегибается" через нее (рис.6).

ТЕОРЕМА 1(необходимое условие существования точки перегиба). Пусть график функции у = f(x) имеет перегиб в точке M(x₀, f(x₀)) и функция f(x) имеет в точке x₀ непре­рывную вторую производную. Тогда

(8)

Условие f"(x₀) = 0 не всегда означает нали­чие точки перегиба на графике функции у = f(x). Например, график функции у = x²ⁿ (п > 1) не имеет перегиба в точке (0, 0), хотя при х = 0 вторая производная равна нулю. Потому равенство (8) является только необходимым условием пере­гиба. Точки графика, для которых условие (8) выполнено, называют критическими.

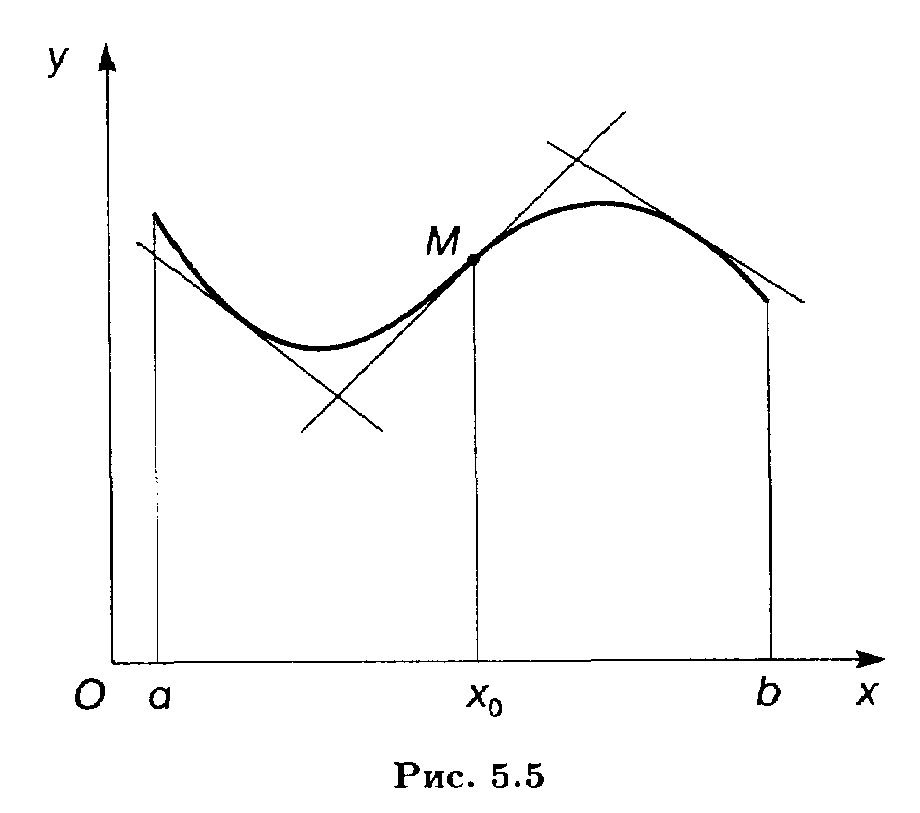
Рис.6

ТЕОРЕМА 2 (достаточное условие существования точки пе­региба). Пусть в некоторой окрестности точки x₀ вторая производная функции у = f(x) имеет разные знаки слева и справа от x₀. Тогда график у = f(x) имеет перегиб в точке М(x₀, f(x₀)).

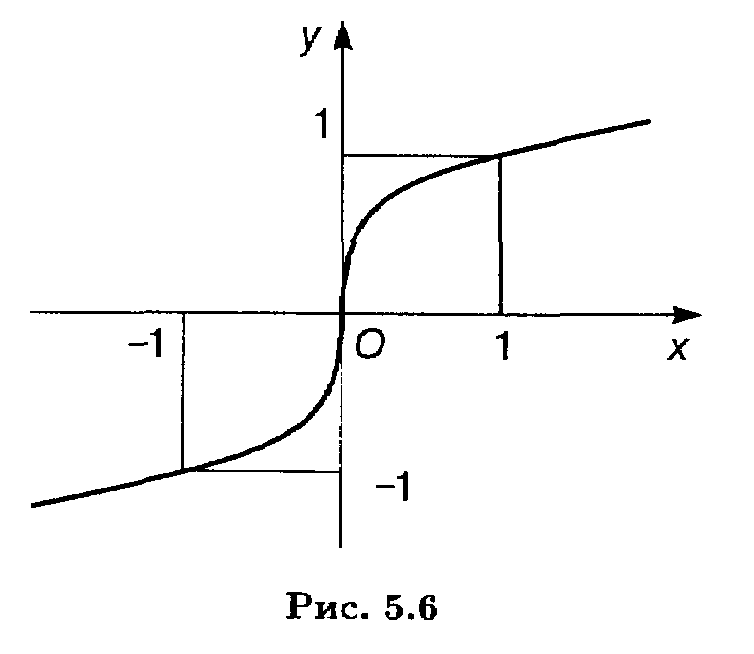
Рис.7

Пример: f(x) = ехр (-x²).

Решение. Последовательно находим f'(x)= -2x exp(—x²), f"(x) = 2 exp (-x²)(2x² — 1). Приравнивая вторую производ­ную к нулю, получаем критические точки х = ±1/ . Вви­ду зависимости функции от х² достаточно исследовать точку x = l/ . Нетрудно видеть, что при переходе через эту точку слева направо f"(x) меняет знак с минуса на плюс. Следова­тельно, на левой ветви функции точка M₁(-1 / , e^-1/2) явля­ется точкой перегиба графика функции со сменой выпуклости вниз слева на выпуклость вверх справа (рис.8). На правой ветви в точке перегиба М₂(1/ , е^-1/2) графика функции име­ет место смена выпуклости вверх слева на выпуклость вниз справа.

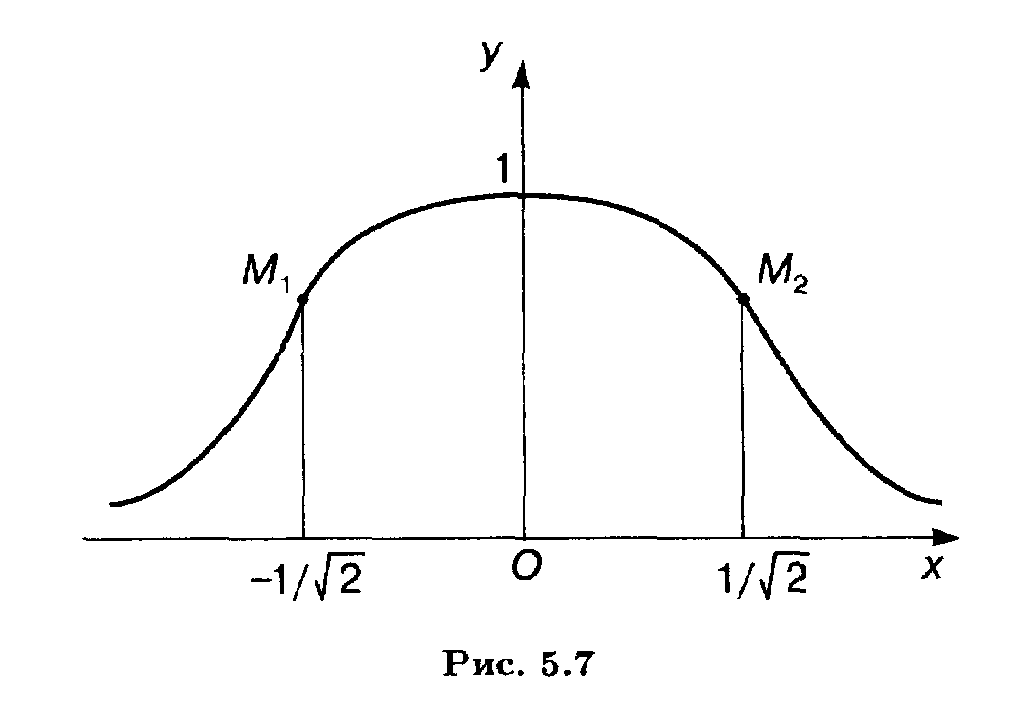
Рис.8

Асимптоты графика функции

Определение. Прямая х = а называется вертикальной асимптотой графика функции у = f(x), если хотя бы одно из предельных значений f(x) или f(x) равно + или - .

Вертикальные асимптоты обычно сопутствуют точкам раз­рыва второго рода. Например, график функции у = е^1/x име­ет вертикальную асимптоту х = 0, так как f(x) при х 0+.

Определение. Прямая у = kx + b называется наклонной асимптотой графика функции у = f(x) при х ± , если f(x) можно представить в виде

(9)

где α(х) 0 при х ± .

(10)

Из равенства (9):

(11)

Пример: f(x) = .

Решение. Найдем вертикальную асимптоту. Точка x = -1 является точкой разрыва 2-го рода, причем

Затем находим наклонные асимптоты:

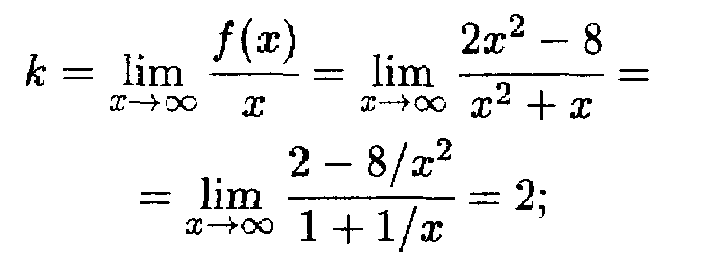
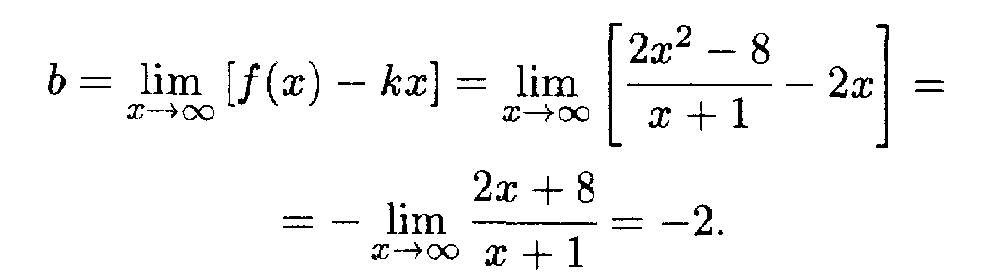
Таким образом, получаем уравнение наклонной асимптоты

Схема исследования графика функции

1. Найти область определения функции.

2. Определить возможный тип симметрии функции: чет­ность или нечетность функции. Функция f(x) называется чет­ной, если выполнено условие симметрии ее графика относи­тельно оси Оу:

(12)

Функция f(x) называется нечетной, если выполнено условие симметрии ее графика относительно начала координат O (0, 0):

(13)

При наличии симметрии достаточно построить график функции на правой координатной полуплоскости и затем ото­бразить его на левую половину: зеркально относительно оси Оу в случае (12) (рис. 9,а) или с центральной симметрией в случае (13) (рис.9,б).

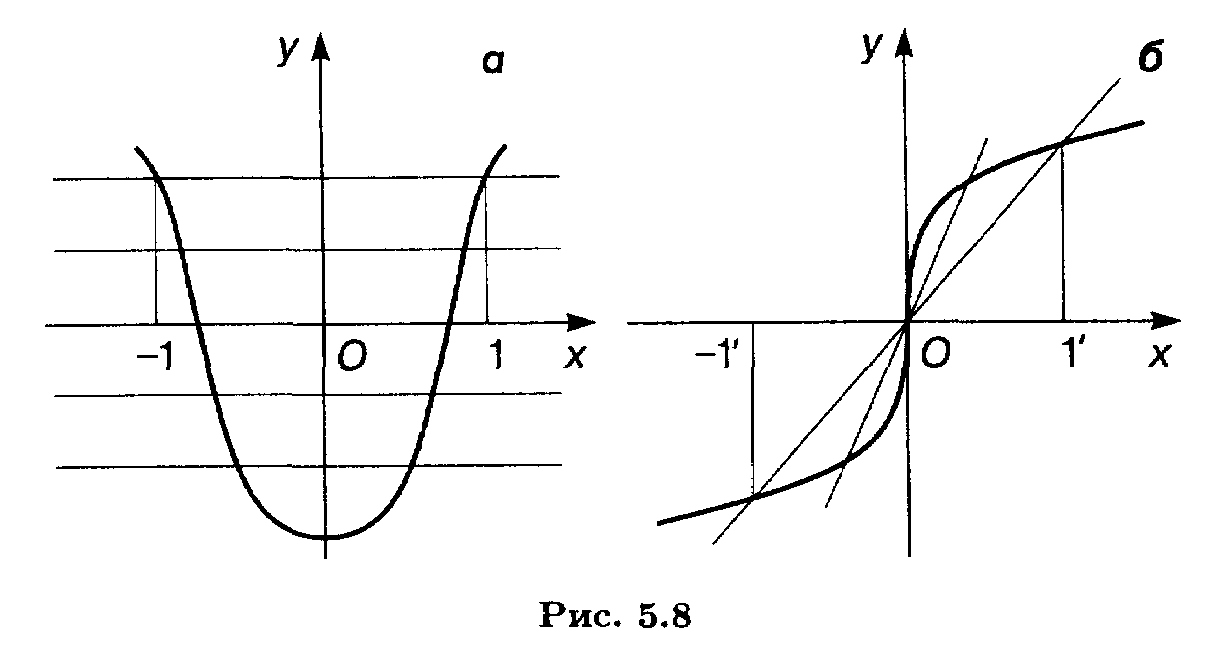
Рис.9

3. Найти точки пересечения графика функции с осями коор­динат Ох и Оу, т.е. решить соответственно уравнения у = f(0) и f(x) = 0.

4. Найти асимптоты.

5. Найти точки возможного экстремума.

6. Найти критические точки.

7. Исследовать знаки первой и второй производных, опреде­лить участки монотонности функции, направление выпуклос­ти графика, точки экстремума и перегиба.

8. Определить максимум и минимум функции на области ее определения. Если областью определения функции является отрезок [а, b], необходимо вычислить значения функции в его концах и сопоставить их с локальными экстремумами.

9. Построить график функции с учетом проведенного ис­следования.

Пример: Исследовать и построить график функции

(14)

Решение. Действуем по приведенной выше схеме.

1. Область определения функции: х ≠ 0 или х (- , 0) (0, ).

2. Функция (14) является нечетной, так как f(-x) = - f(x).

3. Уравнение f(x) = 0 дает корни х = ±1 (точки пересече­ния с осью Ох). Пересечения с осью Оу нет в силу п.1.

4. Имеется вертикальная асимптота — ось Оу, так как пре­дел f(x) при х 0 бесконечен: f(x) + при х 0-, f(x) - при х 0+.

Определяем наклонную асимптоту:

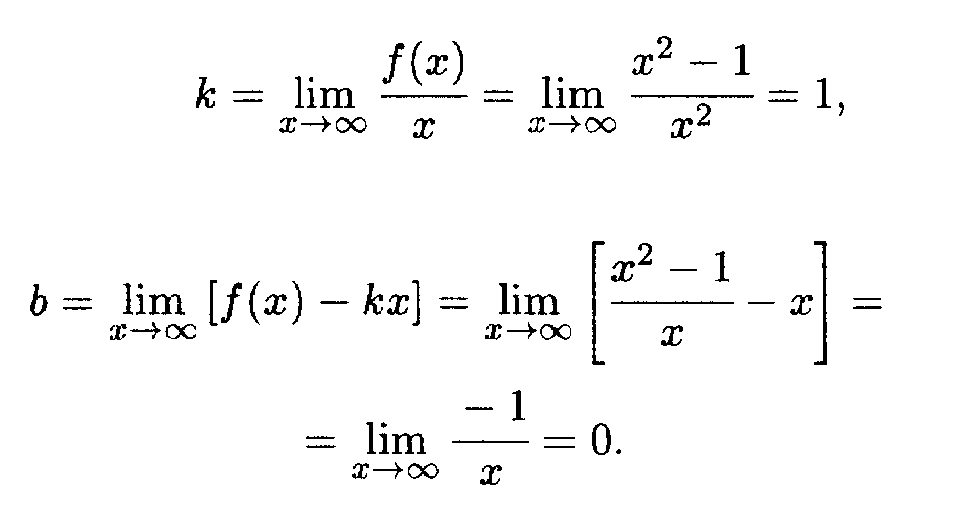
Итак, уравнение наклонной асимптоты: у = х.

5. f'(x) = , т.е. производная нигде не равна нулю и точек возможного экстремума нет. В области определения везде f'(x) положительна.

6. f"(x) = —2/х³ — критических точек нет.

7. Функция (14) монотонно возрастает на всей области своего определения, так как ее производная всюду положитель­на. В левой координатной полуплоскости выпуклость графика функции направлена вниз (f"(x) > 0), в правой полуплоскости выпуклость направлена вверх (f"(x) < 0).

8. Наибольшего и наименьшего значений функции не су­ществует, поскольку область ее значений неограничена.

9. График функции (14) приведен на рис.10.

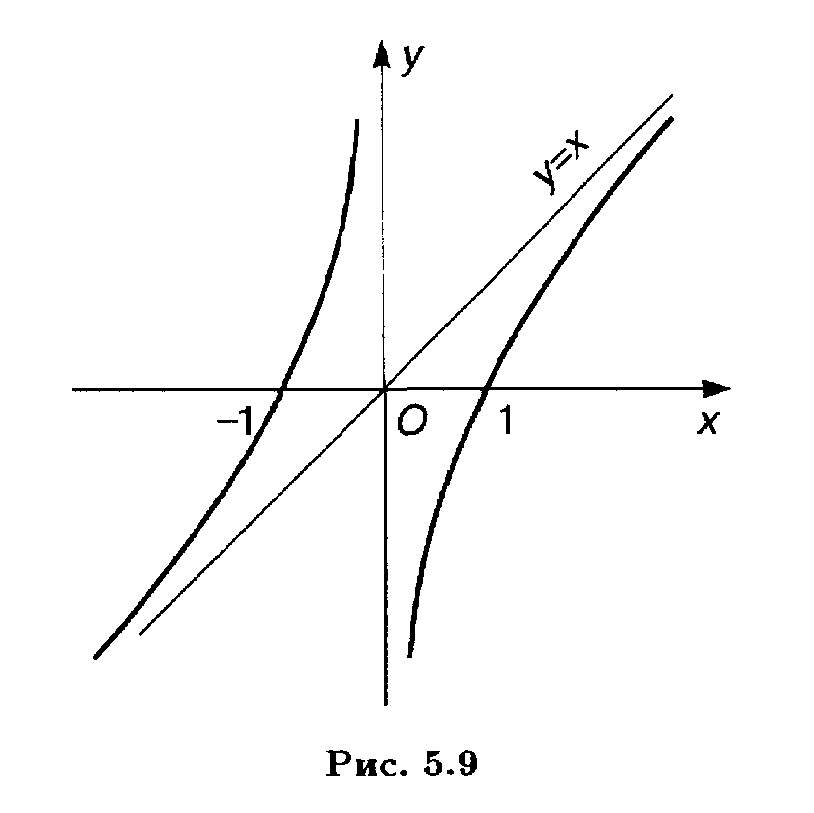
Рис.10