22

Дифференцирование сложной функции

ТЕОРЕМА. Пусть функция х = φ(t) имеет производную в точке t₀, а функция у = f(x) имеет производную в соответ­ствующей точке x₀ = φ(t₀). Тогда сложная функция f[φ(t)] имеет производную в точке t₀ u справедлива следующая фор­мула:

(1)

(Для случая суперпозиции двух функций, где у зависит от t через одну промежуточную переменную х).

Если у зависит от t через две промежуточных переменных (у = у(х), х = φ(u), u = ψ(t) ), то производная y'(t) вычисляется по формуле

(2)

Задание: Найти производную функции у = tg (x³).

Понятие производной n-го порядка

Обозначение производных высших порядков: у", у'", у⁽⁴⁾, у⁽⁵⁾, ..., у⁽ⁿ⁾ (для второй, третьей, четвертой, пятой….., n-й производных соответственно) или вместо у пишут f(x): f"(x), f"(х), ..., f⁽ⁿ⁾(x).

Производная n-го порядка – это производная от производной (n — 1)-го порядка: y⁽ⁿ⁾ = (y^(n-1))'.

Пример 1. Найти производную второго порядка от функции у = х³ + 2х.

Решение. Последовательно находим первую производную, а затем и производную от нее:

Формулы для вычисления производ­ных n-го порядка для функций sin х и cos х:

(3)

Применение производных в исследовании функций Раскрытие неопределенностей Правило Лопиталя

Отношение двух функций при x a есть неопределенность вида , если

Раскрыть эту неопределенность означает вычислить предел , если он существует.

ТЕОРЕМА (теорема Лопиталя). Пусть функции f(x) и g(х) определены и дифференцируемы в некоторой окрестнос­ти точки а за исключением, быть может, самой точки a. Кроме того, пусть , причем g'(х) ≠ 0 в указанной окрестности точки а. Тогда если существует предел отношения (конечный или бесконечный), то существует и предел , причем справедлива формула

=

Эту теорему обычно называют правилом Лопиталя.

Замечание 1. Правило Лопиталя можно применять повторно, если f'(x) и g'(х) удовлетворяют тем же требо­ваниям, что и исходные функции f(x) и g(х).

Замечание 2. Теорема остается верной и в случае, когда x→∞ (х ± ).

Неопределенности вида

Отношение двух функций при х а называется неопределенностью вида , если (- или + ).

Правило Лопиталя остается справед­ливым при замене условия на условие .

Пример: Найти lim x/e^x

x→∞

Решение: lim x/e^x = [∞/∞] = lim x^'/(e^x)' = lim 1/e^x = 0

x→∞ x→∞ x→∞

Другие виды неопределенностей

Неопределенности вида 0 ∙ и — можно свести к неопределенностям вида и . Покажем это на примерах.

Пример: Найти предел x ln x.

Решение. Здесь неопределенность вида 0 ∙ . Преобразуем функцию под знаком предела: х ln х = и теперь уже имеем неопределенность вида при х 0+. Теперь, применяя правило Лопиталя, получаем

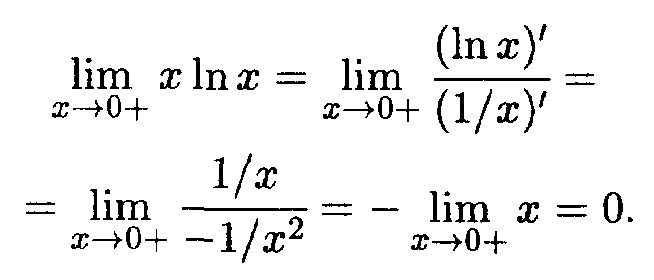
Пример : Найти (cosec x — ctg x).

Решение. Это неопределенность вида — . Преобразуя функцию под знаком предела, получаем

(4)

Неопределенность (4) вида при х 0. Согласно правилу Ло­питаля

Рассмотрим неопределенности вида 0⁰, 1 , ⁰, возникаю­щие при вычислении пределов функций у = и(х)^v(x). Неопреде­ленности этого вида сводятся к неопределенности вида 0 ∙ с помощью тождественного преоб­разования

(5)

Пример : Найти предел .

Решение. Это предел вида 0⁰; используя формулу (5), имеем с учетом решения первого примера

Пример: Найти предел

Решение. Это предел вида 1 . Найдем предел функции у = ctg x ln(1 + x) при x 0. В соответствии с представлением (5) имеем следующую цепочку равенств:

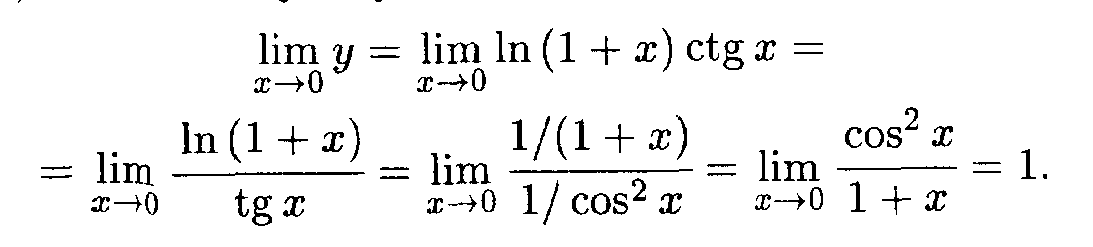
Следовательно, искомый предел равен