
- •Графическое дифференцирование
- •§ 1. Геометрический смысл производной
- •§ 2. Графическое дифференцирование
- •П р. 2 Теперь рассмотрим случай, когда отдельные участки графика функции являются произвольными кривыми, не являющимися квадратичными параболами.
- •§ 3. Признаки существования локальных экстремумов и точек перегиба. Графическая иллюстрация.
- •§ 4. Графическое дифференцирование. Типовые задания.
§ 3. Признаки существования локальных экстремумов и точек перегиба. Графическая иллюстрация.
Определение 1. Дифференцируемой точкой функции назовем такую точку на графике функции, в которой существует конечная производная функции ( существует касательная, не направленная вертикально).
Определение 2. Недифференцируемой точкой функции назовем такую точку на графике функции, в которой или не существует производная функции (не существует
касательная, касательная справа и касательная слева не совпадают), или производная обращается в бесконечность (касательная вертикальная).
В соответствии с введенными определениями можно ввести понятие локального дифференцируемого и недифференцирруемого экстремумов, графическое изображение которых дано на Рис. 1
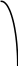 y
Рис.
1
y
Рис.
1
 E
R
E
R


 C
C

 A
A
D F х
B G
Точки на графике A, B – точки дифференцируемого экстремума (максимума и минимума, соответственно). Точки С, D, E, F, G, R – точки недифференцируемого экстремума ( C, E, R – точки максимума; D, F, G – точки минимума).
Проиллюстрируем с помощью графического дифференцирования справедливость необходимого и достаточных признаков существования локального экстремума функции.

 y
y
y
y

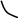
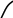
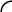
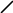

 x x
x x
Дифференцируемые экстремумы Недифференцируемые экстремумы

 y'
y'
y'
y'


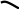
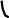

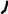

(+) (+) + +

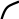



 0
( +) 0
x
(+) + +
x x
0
( +) 0
x
(+) + +
x x
 (-)
(-) (-) (-) (-)
( -) (-) -
(-)
(-) (-) (-) (-)
( -) (-) -

 y''
y''
y''
y''




 (+)
x (+) +
+ (+) x
(+)
x (+) +
+ (+) x

 (-)
(-) (-)
(-)
(-)
(-) (-)
(-)
Рис. 2 Рис. 3
Из Рис. 2, можно увидеть, что в точке локального дифференцируемого экстремума производная равна нулю. Причем в точке минимума первая производная меняет знак с минуса на плюс, а в точке максимума с плюса на минус. Вторая производная в точке минимума положительна, а в точке максимума отрицательна.
Из Рис. 3, видно, что для недифференцируемых экстремумов первая производная меняет знак также, как и в случае дифференцируемого экстремума, т. е. для минимума меняет знак с минуса на плюс, а для максимума с плюса на минус, однако, конечно, в самой точке экстремума производной не существует.
Заметим, также, что из рисунков следует: если график функции имеет выпуклость вниз, то соответствующая вторая производная положительна, и наоборот, если график имеет выпуклость вверх, то вторая производная отрицательна.
Для читателя оставляем возможность с помощью графического дифференцирования самостоятельно изучить поведение второй производной в дифференцируемой и недифференцируемой точках перегиба.
