Согласно с (4.5) получаем, что

Подставляя полученные выражения для х₁, х₂, х₃ в пятое уравнение системы (4.7), приходим к квадратному уравнению относительно z₁:

0.0353 z₁² + 2.6572 z₁ - 248.7813 = 0, (4.8)

откуда z₁ = - 83.9846  -84; z₁ = 83.9151  84.

Для корня z₁ = 84 получаем, что х₁ = 0,4500; х₂ = 0,3202; x₃ = 0,2298. Для корня z₁ = - 84 имеем, что значение х₁ = -0.1716 < 0, то есть корень z₁ квадратного уравнения (4.8) нас не удовлетворяет.

Исходя из найденных долей акций А₁, А₂ и А₃, получаем, что сформированный ПЦБ имеет риск:

Его ожидаемая (максимально возможная при данных условиях) норма прибыли

т_П^* = х₁т₁ + х₂т₂ + x₃т₃ = 52.202(%).

2. Включение в портфель безрискованных ценных бумаг

Решение задачи формирование оптимального ПЦБ приобретает новых особенностей, если учесть факт существования на рынке как рисковых, так и безрисковых ЦБ (или почти безрисковых) типа государственных обязательств с фиксированной нормой прибыли.

А потому возникает задача правильного распределения капитала между безрисковыми и рисковыми вложениями.

Пусть х — доля капитала, которую инвестор разместил в виде портфеля Е(m_E; _E), сформированного на основе рискованных вложений. Тогда (1 - х) — доля средств, размещенная под фиксированный процент R_F, в безрисковые ЦБ. Норма прибыли от такого размещения капитала составит:

R_П = (1- х) R_F + х R_Е,

а ожидаемая норма прибыли —

m_П = (1 – x) R_F + xm_E

Риск такого размещения характеризуется величиной

Поскольку для безрисковых ЦБ _F = 0, _EF = 0, то

то есть величина доли х удовлетворяет соотношение:

Тогда

Уравнение

или же

(4.9)

является уравнениями прямой в двумерном пространстве (т - σ). Эта прямая называется линией рынка капиталов и характеризует ПЦБ, которые состоят как из безрискованных ЦБ, так и с ЦБ, отягощенных риском.

Если Е(т_Е; σ_Е) – это точка касательной линии рынка капиталов к множеству эффективных портфелей (рис. 4.3), то эту точку называют рыночным (эффективным) портфелем.

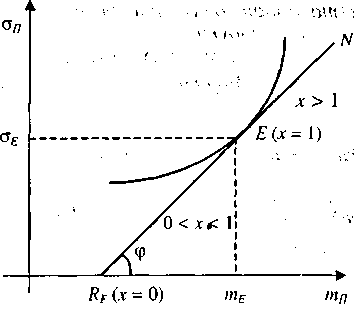
Рис. 4.3. Учет в ПЦБ безрисковых ценных бумаг

На рис. 4.3 прямая R_FN (линия рынка капиталов) представляет собой множество оптимальных решений, которые характеризуются пропорциональным (постоянным) соотношением прироста нормы прибыли к возрастанию степени риска.

Если х = 0, то это означает, что весь капитал инвестор вкладывает в безрисковые ЦБ. Если же х = 1, то это означает, что весь капитал вкладывается в рыночный портфель Е(т_Е; σ_Е).

В случае, если 0 < х < 1, то задачу распределению капитала между рисковыми и безрисковыми ЦБ можно рассматривать как ситуацию предоставления кредита (инвестирование) под фиксированный процент R_F.

Величина х > 1 в случае, если инвестор может воспользоваться ссудой и инвестировать в рыночный портфель Е(т_Е;σ_Е) большее, чем величина его собственного начального капитала (получение кредита).

3. Расчет структуры рыночного портфеля.

Запишем уравнения (4.9) в виде:

Поскольку — модифицированный коэффициент вариации рыночного портфеля Е(т_Е;σ_Е), имеет отрицательный ингредиент ( = ), то задача расчета его структуры сводится к нахождению такого портфеля из множества допустимых портфелей, который удовлетворял бы условие:

,

где x = (x₁, x₂, …, x_N);

Другими словами, рыночным является такой ПЦБ из множества допустимых портфелей, который обеспечивает минимум отношения между: возрастающей степенью риска и дополнительной прибылью по сравнению с ЦБ, которые имеют фиксированную норму прибыли.

Решение поставленной задачи сводится к решению системы линейных алгебраических уравнений:

, (4.10)

где y_i = λ · х_i, i = 1, ..., N .

Учитывая, что

,

получаем:

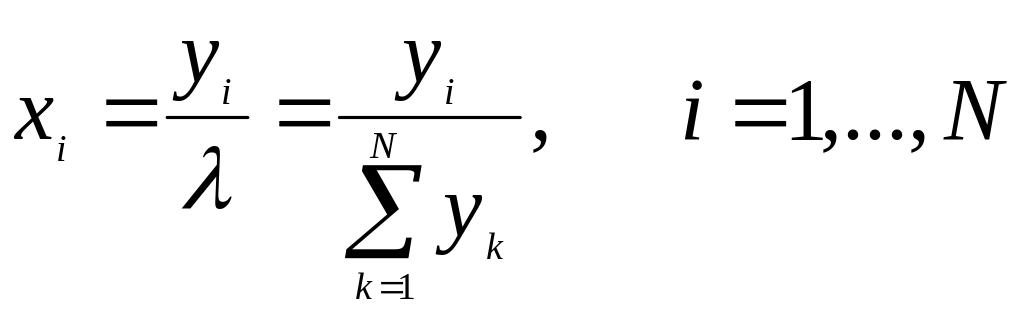
Пример 4.4. Из акций вида А₁ А₂, А₃, описанных в примере 4.1 (ожидаемые нормы прибыли этих акций составляют соответственно 60%, 50% и 40%; риски - 40%, 30%, и 25%; коэффициенты корреляции - ρ₁₂ = 0.2; ρ ₁₃ = - 0,3; ρ ₂₃ = - 0,5), сформировать рыночный (эффективный) ПЦБ, если норма прибыли государственных облигаций (которые являются почти безрисковыми) составляет 10%.

Решение. С учетом условия задачи приходим к системе уравнений:

Решив эту систему уравнений, получаем, что y₁ = 0,041; y₁ = 0,082; y₃= 0,117. Поскольку λ = y₁ + y₂ + у₃ = 0,24, то:

х₁ = у₁\ = 0,171; х₂ = у₂\ = 0,342; х₃ = у₃\ = 0,487.

Ожидаемая норма прибыли сформированного ПЦБ

т_е = х₁т₁ + x₂m₂ + х₃т₃ = 46,83 (%),

его риск (среднеквадратичное отклонение)

Пример 4.5. (Предоставление кредита). Инвестор сформировал эффективный портфель, рассчитанный в примере 4.4. Он принял решения относительно размещения 75% денежных средств в рыночный портфель, остаток — в ценные бумаги, которые необремененные риском.

Необходимо вычислить ожидаемую норму прибыли и риск портфеля инвестора.

Решение. Поскольку т_Е = 46,84%, _Е =12,388%, R_F =10%, х = 0,75, то

m_П = (1-х)R_F + xm_E = 0,2510 + 0,7546,84 = 37,63(%),

_П = x _E = 0,75  12,388 = 9,291(%).

Пример 4.6. (Получение кредита). Инвестор использует эффективный портфель, рассчитанный в примере 4.4. Он принял решения по размещению капитала в рыночный портфель, который составляет 120% по отношению к собственному капиталу.

Необходимо вычислить долю ссудных средств, ожидаемую норму прибыли и риск его портфеля.

Решение. Поскольку т_Е = 46,84%, _Е =12,388%, R_F =10%, х = 1,2, то m_П = (1-х)R_F + xm_E = (1 - 1,2)  10 + 1,2  46,84 = 54,208(%),

_П = x _E = 1,2  12,388 = 14,866(%).

Доля ссудных средств составляет 20% (20% = 120% - 100%) объема собственного капитала.

Пример 4.7. Инвестор использует эффективный портфель, рассчитанный в примере 4.4. Он принял решения по размещению 120% собственного капитала в рыночный портфель.

Необходимо построить линию рынка капиталов и осуществить соответствующий анализ.

Решение. Поскольку т_Е = 46,84%, _Е =12,388%, R_F =10%, то исходя из соотношения

получаем соответствующее уравнение линии рынка капиталов:

или же

Итак, для эффективного портфеля увеличения риска на 1 % приводит к увеличению его нормы прибыли почти на 3% (на 2,974%).

Если же выходить из соотношения

это получаем такое уравнение:

А потому для эффективного портфеля увеличения нормы прибыли на 1% приводит к увеличению его риска почти на 0,3363%, то есть на величину модифицированного коэффициента вариации (СУ_ЕҐ- = 0,3363).

.

Литература: 1, 3, 4, 9, 10, 11, 12, 18.