Практическое занятие № 4 Управление портфелем ценных бумаг.

(4 часа)

Цель: научится рассчитывать структуру портфеля ценных бумаг в различных экономических ситуациях.

План:

1. Портфель из многих видов ценных бумаг.

1.1. Задача сохранения капитала.

1.2. Задача получения желаемой (фиксированного) прибыли.

1.3. Задача обеспечения прироста капитала.

2. Включение в портфель безрисковых ценных бумаг.

3. Расчет структуры рыночного портфелю.

Рассмотрим примеры решения задач.

1. Портфель из многих видов ценных бумаг

Перейдем теперь к общему случаю, если в состав ПЦБ включено N (N>2) разных акций.

Рассмотрим, например, три акции, которые имеют нормы прибыли соответственно 15%, 10%, 5%, среднеквадратичные отклонения 10%, 7%, 3% и коэффициенты корреляции ₂₃ = - 0,2; ₁₂ = - 0,4; ₁₃ = + 0,6.

В системе координат т_П – σ_П (норма прибыли — риск, рис. 1) построим точки А₁, А₂, А₃, что отвечают однородным ПЦБ, сформированным из соответствующих акций. На этом же рисунку построим линии (дуги), которые отвечают ПЦБ, сформированному из двух видов акций (А₃А₁; А₃А₂; А₂А₁).

Рис. 1. Множество допустимых портфелей ценных бумаг

Точкам К  А₃А₂ и L  А₂А₁ отвечают определенные ПЦБ, сформированные из двух (соответственно А₃, А₂ и А₂, А₁) видов акций. Для этих портфелей можно рассчитать нормы прибыли и риски. Будем считать теперь, что любой из этих портфелей является определенного вида «ценной бумагой» соответственно К и L. А потому, в свою очередь, можно сформировать новый ПЦБ для ЦБ К и L. Такие ПЦБ уже будут включать по три акции (А₁, А₂, А₃) и им отвечает дуга KL.

Размышляя таким образом, прийдем к выводу, что каждая точка, которая принадлежит к заштрихованной области (рис. ), отвечает некоторому ПЦБ, сформированному из трех видов акций.

Допустимым множеством ПЦБ называется область, точки которой характеризуют степень риска и норму прибыли портфеля всех возможных долей отдельных акций в портфеле (на рис. — это область, ограниченная жирной линией.).

Особенностью дуги О*А₁, которая належит допустимому множеству, есть то, что для любой точки этой дуги нельзя указать другой точки допустимой области, для которой ПЦБ был бы лучшей.

Эффективным множеством ПЦБ называются те портфели, которые отвечают точкам дуги О^*A₁. То есть эффективным портфелем считается такой, для которого в допустимом множестве ПЦБ нельзя указать другого портфеля:

• с тем же значением величины ожидаемой нормы прибыли и меньшей степенью риска;

• с тем же значением величины риску и большим значениям ожидаемой нормы прибыли.

Очевидно, что для ПЦБ, составленных из двух акций, допустимое множество совпадает с множеством эффективных портфелей, и они составляют дугу О^*A₁ (рис. 1).

Рассмотрим теперь общий случай построения ПЦБ, сформированного из N ЦБ. Как и раньше, обозначим через R_k, т_k = М(R_k), σ_k — соответственно норму прибыли, ожидаемую норму прибыли и риск k-ой ЦБ, k = 1, ..., N; через ρ_kj - коэффициент корреляции между k-тым и j-тым видом ЦБ.

1.1. Задача сохранения капитала

Сущность ее состоит в выборе такой структуры ПЦБ, чтобы риск этого портфеля был минимальным. Формальная постановка этой задачи такая:

;

x₁ + … + x_n =1;

x_k  0, k=1, … , N.

Решением задачи отвечает точка О* на рис. 2.

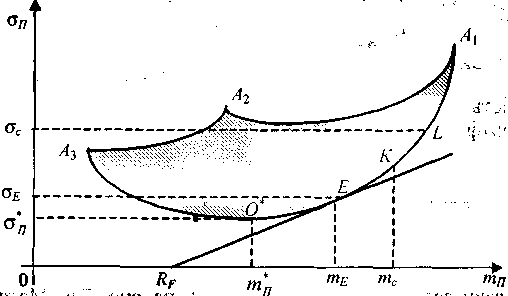
Рис. 2. Геометрическая интерпретация задач по формированию разных видов ПЦБ.

Метод нахождения структуры ПЦБ, которое удовлетворяет условие поставленной задачи, базируется на построении и нахождении точки минимума соответствующей функции Лагранжа, которое, в свою очередь, сводится к решению следующей системы линейных алгебраических уравнений:

(4.1)

Здесь  — дополнительная переменная (неизвестная величина) появление которой вызвана использованием метода Лагранжа.

Следует иметь в виду, что метод Лагранжа, предложенный для решения поставленной задачи, не учитывает ограничений относительно того, что х_k  0; k = 1, ..., N. А потому решение системы (1) необходимо проанализировать с этой позиции.

Обозначим через X^* = {х₁^*; х₂^*;...; х_N^*} решение системы (1). Если все компоненты вектора X^* является положительным (х_k^* > 0, k = 1, ..., N) то этот вектор описывает структуру оптимального ПЦБ, которое отвечает точке О* (рис.3).

Если среди компонент X* окажутся отрицательные, то в искомый ПЦБ не включается та ЦБ, доля которого отрицательна и наименьшая среди полученных отрицательных долей. После изъятия этого ЦБ снова рассчитывается структура оптимального ПЦБ, составленного с (N-1) ЦБ. Процесс изъятия такого рода «неблагоприятных» ЦБ продолжается до тех пор, пока доли всех ЦБ, включенных в портфель, не станут положительными.

Пример 4.1. Ожидаемые нормы прибыли акций вида А₁, А₂, А₃ и А₄ составляют соответственно 60%, 50%, 40% и 70%. Риски этих акций составляют 40%, 30%, 25% и 50%. Тесноту связи между нормами прибыли этих акций отображают коэффициенты корреляции ρ₁₂ = 0.2; ρ ₁₃ = - 0,3; ρ ₂₃ = - 0,5; ρ _И4 = 0,9; ρ ₂₄ = 0,7; ρ₃₄ = - 0,3.

Необходимо сформировать из этих акций ПЦБ, который имеет минимальный риск. Оценить его ожидаемую норму прибыли и ее риск.

Решение. В соответствии с условием задачи

N = 3; σ₁₂ = σ₂₁ = σ₁ σ₂ ρ₁₂ = 0,24030 = 240;

σ₁₃ = σ₃₁ = -300; σ₁₄ = σ₄₁ = 1800; σ₂₄ = σ₄₂ = 1050;

σ₂₃ = σ₃₂ =-375; σ₃₄= σ₄₃=-375;

σ₁₁ = σ₁² = 1600; σ₂₂ = σ₂² = 900;

σ₃₃ = σ₃² = 625; σ₄₄ = σ₄²= 2500.

В соответствии с (4.1) получаем систему уравнений:

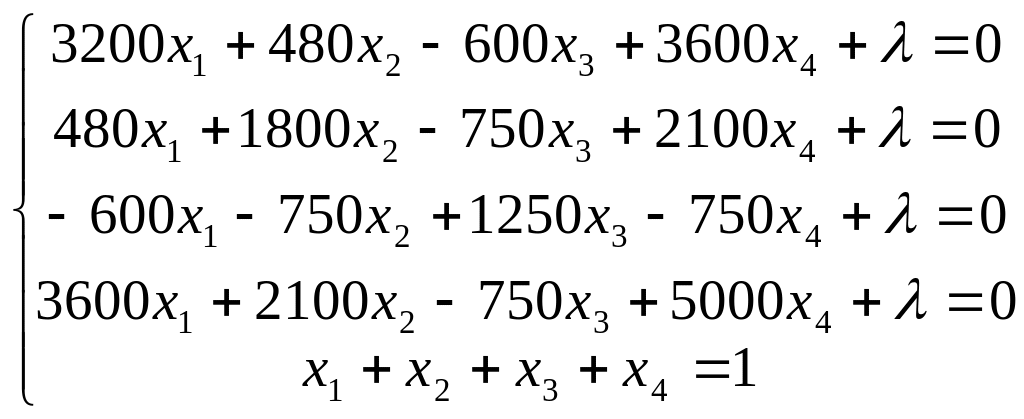
Решив полученную систему уравнений, находим: x₁ = 2,412; x₂ = 1,768; х₃ = - 0,402; х₄ = - 2,778. Поскольку х₄ = - 2,778 — это наименьшее отрицательное число, то в дальнейшем акцию вида А₄ в ПЦБ не включаем. Для акций вида А₁, А₂ и A₃ составляем новую систему уравнений:

В соответствии с последней системой уравнений получаем, что х₁ = 0,1392; х₂ = 0,3453; х₃ = 0,5155.