Глава 1. Кинематика

1.1. Основные понятия кинематики

Кинематикой называется раздел механики, изучающий движение тел без учета причин, вызвавших это движение.

Для описания движения тел, в зависимости от условий конкретных задач, в механике используются различные физические модели, в которых из всего многообразия проявлений движения выделены главные, определяющие характер движения. Простейшей моделью является материальная точка.

Материальная точка – это абстрактная модель реального тела, которое в данной задаче можно принять за геометрическую точку с массой равной массе тело. Тело можно считать материальной точкой, если его размерами можно пренебречь по сравнению с масштабами движения.

Движение тел происходит в пространстве и во времени. Поэтому для описания движения материальной точки надо знать, в каких местах пространства эта точка находилась и в какие моменты времени она проходила то или иное положение.

Тело отсчета – это тело, относительно которого рассматривается движение.

Система отсчета – это тело отсчета, связанная с ним система координат и выбранный способ измерения времени (часы).

Траектория – это линия, которую описывает движущаяся материальная точка в пространстве.

Пройденный путь - длина траектории. Это скалярная величина l , [l]=м.

Перемещение – это вектор , соединяющий начальное и конечное положение точки.

Видно, что только при прямолинейном движении.

Радиус вектор – это вектор соединяющий начало координат и данную движущуюся точку.

.

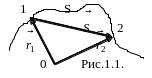
Т.е. перемещение точки равно изменению ее радиус вектора. Если совместить точку О с т.1, то перемещение будет равно самому радиус вектору. , , .

В декартовой системе координат

Для того чтобы знать положение точки в пространстве необходимо в каждый момент времени знать ее координаты или ее радиус вектор. Движение материальной точки может быть задано следующими способами: а) координатным - уравнения движения, б) векторным: (он эквивалентен координатному). При известной траектории возможен еще один способ в) траекторный (естественный) . (рисунок!)

1.2. Скорость и ускорение точки

Пусть положение материальной точки задано радиус-вектором . При движении материальной точки ее радиус-вектор меняется в общем случае, как по величине, так и по направлению. Для характеристики быстроты изменения перемещения вводится понятие скорости точки.

Сред­няя скорость – это отношение вектора перемещения точки к соответствующему промежутку времени

` υ_ср = ∆ / ∆t.

Часто используют и путевую среднюю скорость, равную пути, пройденному точкой в единицу времени

υ _ср=∆l/∆t.

Очевидно, что чем меньше будет промежуток времени ∆t, для которого вычислена средняя скорость, тем величина _ср будет точ­нее характеризовать движение точки. Чтобы получить точную характеристику движения, вводят понятие о (мгновенной) скорости точки в данный момент времени.

Скорость - вектор­ная величина, к которой стремится средняя скорость _ср при стрем­лении промежутка времени ∆t к нулю

υ = (`υ<sub>ср</sub>)= . `υ= .

Вектор скорости материальной точки в данный момент времени равен производной от радиус-вектора по времени.

Скорость точки всегда направлена по касательной к траектории ее движения.

Для характеристики изменения скорости вводится понятие ускорения точки.

Ускорение - вектор­ная величина, к которой стремится среднее ускорение _ср= ∆ / ∆t при стрем­лении промежутка времени ∆t к нулю

= .

Вектор ускорения материальной точки в данный момент времени равен производной от скорости по времени.

Вектор ускорения всегда направлен в сторону вогнутости траектории.

Определения `υ и `а, содержат производные по времени от векторов `r и `υ. Переход к зависимостям между их проекциями осуществляется с помощью следующей теоремы: про­екция производной от вектора на ось равна производной от проекции данного вектора на ту же ось.

Учитывая, что в декартовой системе координат rx=х, ry =у, r_z=z, находим

υ_x= , υ_y = , υ_z =

или

υ_x= , υ_y = , υ_z= ,

где точка над буквой означает дифференцирование по времени.

Зная проекции скорости, найдем ее модуль и направление (т. е. углы a, b, g, которые вектор образует с координатными осями)

Совершенно аналогично

а_x = , а_y = , а_z = .

или

а_x = , а_y = , а_z =

Модуль и направле­ние ускорения найдутся из формул

,

где , , — углы, образуемые вектором ускорения с коорди­натными осями.