Построение сложного выражения

В алгебре логики занимаются исследованием общих схем построения сложных высказываний. Высказывания обозначаются большими латинскими буквами.

Например:

«Если мы купим красные помидоры, то они будут спелые и вкусные»

А= «Мы купим красные помидоры»

В= «Помидоры будут спелые»

С= «Помидоры будут вкусные»

Тогда, структура высказывания будет: D = А → В • С

«Двери бывают с витражами или без них»

А= «Двери бывают с витражами»

В= «Двери бывают без витражей»

Тогда, структура высказывания будет: D = А + В

Упражнение

Составить структуру по следующим высказываниям:

1. Если не пойдет дождь, то не будет пасмурно и сыро.

2. Если мы соберем хворост или сухой травы, то разожжем костер и вскипятим чай.

Урок 3-4. Построение таблиц истинности сложных выражений

Под логическим выражением понимают запись, которая может принимать логическое значение «истина» или «ложь». Логические выражения могут включать в себя функции, алгебраические операции, операции сравнения и логические операции.

В логике, как и в математике, существует приоритет выполнения операций:

Действия в скобках выполняются в первую очередь!

Если скобок нет, то тогда:

1. Отрицание

2. Логическое умножение

3. Логическое сложение

4. Импликация, эквиваленция

Упражнение

1. Построить таблицу истинности сложного выражения:

1. не(неА+В)+неС

2. не(А•В)•неС

3. не(А+неВ+С)

2. Какое логическое выражение равносильно выражению не(А+неВ)?

1. неА•В

2. не(А•В)

3. неА•неВ

4. неА+В

3. Какое логическое выражение равносильно выражению неА+А•неВ?

1. неА+В

2. неА•В

3. не(А•В)

4. не(А+В)

4. Какое логическое выражение равносильно выражению не(А+В)•неС?

1. неА+В+С

2. неА•неВ•С

3. не(А•В•С)

4. не(А+В+С)

Урок 5-6. Законы логики

В алгебре логики выполняются основные законы, позволяющие производить тождественные преобразования логических выражений. Доказательства законов можно произвести на основании таблиц истинности для записей правой и левой стороны равенства соответственно. Законы алгебры логики служат для упрощения формул или приведения их к определенному виду. Под упрощением формулы, не содержащей операций импликации и эквивалентности, понимают равносильное преобразование, приводящее к формуле, которая содержит либо меньшее число операций (по сравнению с исходной), либо меньшее число переменных.

Закон	Описание	Для логического сложения	Для логического умножения
Переместительный (коммутативность)	Независимость от перестановки	А+В=В+А	А•В=В•А
Сочетательный (ассоциативность)	Независимость от порядка выполнения однотипных операций	А+(В+С)=(В+А)+С	А•(В•С)=(В•А)•С
Распределительный (дистрибутивность)	Правила раскрытия скобок и вынесение за скобки	А•(В+С)=(А•В)+(А•С)	А+(В•С)=(А+В)•(А+С)
Законы де Моргана	Отрицание вариантов, отрицание одновременной истинности
Идемпотенции	Отсутствие степеней и коэффициентов	А+А=А	А•А=А
Поглощения		А+(А•В)=А	А•(А+В)=А
Поглощения отрицания		А+(Ā•В)=А+В	А•(Ā+В)=А•В
Склеивания		(А•В)+(Ā•В)=В	(А+В)•(Ā+В)=В
Преобразования импликации	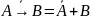	или А→В=А•В
Закон исключенного третьего и закон противоречия	Инверсия	А+Ā=1	А•Ā=0
Операции с константами	Действия с абсолютно- истинными и абсолютно- ложными высказываниями	А+0=А А+1=1	А•1=А А•0=0
Инволюция	Двойное отрицание	= А

Упражнение

1. Постройте логическую формулу по высказыванию: «Неверно, что если погода пасмурная, то дождь идет тогда и только тогда, когда нет ветра»

2. Упростить выражение:

1. А•не(неВ+С)

2. не((А+В)→не(В+С))

3. Каково наибольшее целое число Х, при котором истинно высказывание:

(35<X•X)→(X<(X-3))

4. Какое из приведённых имен удовлетворяет логическому условию: (первая буква согласная → вторая буква согласная)•(предпоследняя буква гласная → последняя буква гласная)?