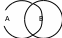Урок 1. Алгебра логики как средство представления информации в пк

Логика («logos») – мысль, слово, разум – наука, изучающая законы и формы мышления

Основоположник логики – древнегреческий ученый Аристотель (384 г. до н.э.). Логика по Аристотелю – это наука о выводе одних умозаключений из других сообразно их логической форме. Логику Аристотеля называют классической или формальной. Постепенно появилась математическая логика, основоположником которой считают Вильгельма Лейбница – немецкого философа и математика. Лейбниц предложил использовать в логике математическую символику и высказал мысль о применении в логике двоичной системы счисления. Большой вклад в развитие логики внес английский математик Джордж Буль. Он создал особую алгебру – алгебру логики или булеву алгебру. Булева алгебра используется для решения сложных математических задач в робототехнике, при разработке компьютеров и программ.

Понятие, отношение между понятиями, объем понятия

Абстрактное мышление – процесс рационального отражения материального мира в понятиях, суждениях, умозаключениях, позволяющих проникнуть в сущность и закономерные связи предметов и явлений, преобразовать их в теории, а затем применить их на практике.

Понятие – форма мышления, в которой отражаются существенные признаки предмета или группы предметов («цветок», «конь», «разрывная пуля»)

Содержание понятия – совокупность признаков, по которым произведено обобщение предметов в понятие.

Объем понятия – совокупность предметов одного понятия, т.е. их количество.

Отношения между понятиями принято представлять в виде круговых схем, которые впервые предложил Леонардо Эйлер (1707-1783) – швейцарский математик, живший в России (круги Эйлера). Каждый круг – понятие, каждая точка внутри круга – предмет в понятии.

Сравнимые (совместимые) понятия – отражают некоторые общие существенные признаки предмета или класса предметов, то есть объемы понятий совпадают полностью или частично.

Виды совместимых понятий:

Эквивалентность – понятия, объемы которых полностью совпадают А – дочь В - внучка	А=В
Перекрещивание (пересечение) – понятия, объемы которых частично совпадают (музыкант, студент)
Подчинение – понятия, объем одного их которых составляет часть другого (энциклопедия, книга) А - родовое понятие (род) В – видовое понятие (вид)

Несовместимые понятия – объемы не совпадают ни в одном элементе, однако могут быть включены в объем общего для них понятия.

Виды несовместимых понятий:

Противоречие – понятия, которые являются видами одного и того же рода, причем первое понятие указывает на определенные признаки, а второе понятие отрицает их (известный факт, неизвестный факт)	А В
Противоположность – понятия, которые являются видами одного и того же рода, и при этом одно из них содержит какие-либо признаки, а другое отрицает эти признаки А – самый низкий результат В – самый высокий результат С – общий результат	А С В
Соподчинение – два или более неперекрещивающихся понятий, принадлежащих общему родовому понятию А – футболист В – баскетболист С - спортсмен